درک تقسیمبندی مشتری برای هدفگذاری متمایز در بازاریابی

اگر شما صاحب یک کسب و کار باشید، حتما با مشتریان زیادی سر و کار دارید. این مشتریان از نظر جمعیت (سن، جنسیت، درآمد)، الگوها و رفتار خرید (تکرار خرید، ارزش پولی و محدوده قیمت خرید، نوع اقلام خریداری شده) و... بسیار متنوع خواهند بود. یکی از این روش‌های رایج تقسیمبندی مشتریان، روش RFM است. RFM که مخفف سه واژه Recency (تازگی)، Frequency (فراوانی) و Monetary Value (ارزش پولی) میباشد، یک مدل تحلیل بازاریابی است که مصرفکنندگان نهایی یک شرکت را بر اساس الگوی خرید یا عادات آنها تقسیمبندی میکند. به طور دقیقتر، آخرین زمان خرید مشتری (تازگی)، تعداد دفعات خرید او (فراوانی) و مقدار مبلغی که مشتری خرید داشته است (ارزش پولی)، سه معیاری هستند که برای تقسیمبندی مشتریان مورد استفاده قرار میگیرد. اکنون، شما به عنوان یک بازاریاب باید تصمیم بگیرید که بر اساس این دادهها، چه نوع تبلیغات و هدف‌گذاری باید انجام شود. این کار، برای مشتریان مختلف متفاوت خواهد بود زیرا گروه‌های مشتریان متفاوت، رفتار متفاوتی دارند. به عنوان مثال برای مشتریان خاصی که بسیار حساس به قیمت هستند،  تبلیغاتی برای محصولات تند مصرف با قیمت پایین هدف قرار داده می‌شود. محصولات تند مصرف قیمت پایین، کالاهایی هستند که با سرعت بیشتری فروخته میشوند و قیمت نسبتا پایینی دارند. یا برای بانوان زیر 30 سال، بیشتر مد و محصولات زیبایی هدف قرار می‌گیرد. روش بازاریابی هدفمند باید بکار گرفته شود؛ چرا که اگر بازاریابی و تبلیغات، متناسب با اولویتهای مشتری باشد، تجربه مشتری را بهبود میبخشد و همچنین شانس خرید آنها را به حداکثر میساند. هدف تقسیم‌بندی مشتری، ایجاد بخش‌ها یا گروه‌های مشتری است که مشابه هم باشند، اما هیچ دو گروهی مشابه نیستند و تا حد ممکن با هم متفاوتند.

شناخت مجموعه داده

در این مقاله از مجموعه داده‌های معروف « shopping mall dataset» استفاده خواهیم کرد.

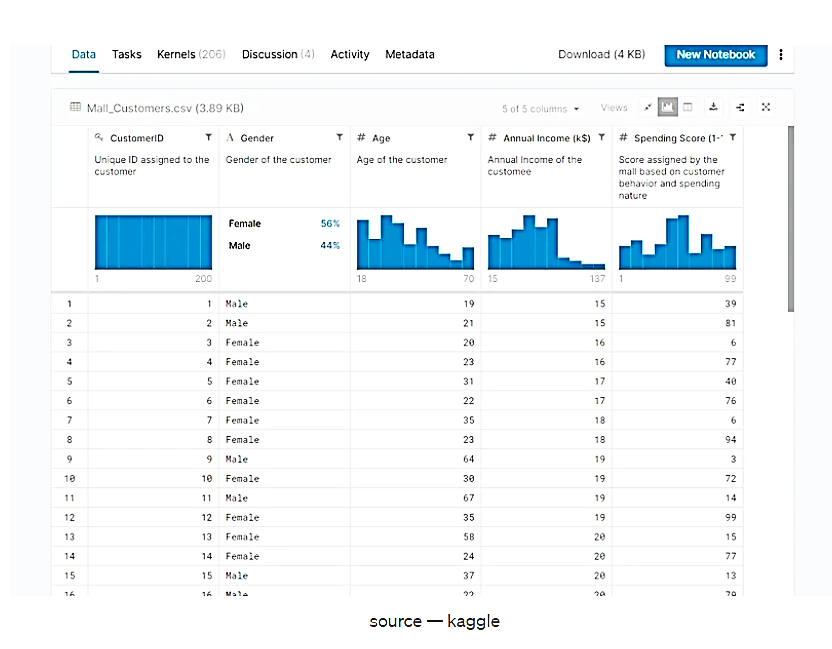
شکل 1. مجموعه داده shopping mall dataset، منبع: kaggle

فرض کنید برای 200 مشتری، اطلاعاتی در رابطه با جنسیت، سن، درآمد و امتیاز هزینه آنها در دسترس است. امتیاز هزینه، یک معیار برای ارزیابی میزان تمایل مشتری به خرید است و در اینجا در مقیاس 1 تا 100 استفاده میشود. امتیاز هزینه بالاتر یعنی مشتری تمایل بیشتری به خرید اقلام دارد و در نتیجه درآمد بیشتری برای مرکز خرید به همراه خواهد داشت. هدف ما این است که این مشتریان را به بهترین نحو گروهبندی کنیم تا مشتریان مشابه با هم گروهبندی شوند و هیچ دو گروهی شبیه به هم نباشند.

چگونه این کار انجام میشود؟ ما اساساً 4 ویژگی مشتری دارید و باید بهترین تقسیمبندی را که میتوانیم بهدست آوریم، انتخاب کنیم. فرض می‌کنیم فقط ویژگی جنسیت را داشتیم، پس طبیعتاً زنان و مردان را به 2 گروه مختلف گروهبندی میکنیم. یا فقط سن مشتری را داشتیم - احتمالاً براکت های سنی (چیزی مانند <18، 18-25، 25-35-35-50،>50 و...) ایجاد میکنیم که بسته به نوع محصولات، منطقی به نظر میرسد. اما زمانی که نیاز داریم مشتریان را بر اساس ویژگیهای متعدد (در اینجا 4 ویژگی) گروه بندی کنیم چه اتفاقی می‌افتد؟ بیایید نگاهی به دادهها بیندازیم و این موضوع را بازتر کنیم.

شک 2. سن در مقابل درآمد- مردان/زنان

اگر شخصی نمودار فوق را ببیند (گراف سن در مقابل درآمد بر اساس «جنسیت»)، احتمالاً به شکل شهودی، بر اساس مرزهای جدایی و برخی زمینههای تجاری گروهبندی زیرا را ارائه میکند:

شکل 3. خوشه 1

در مورد نمودار «امتیاز هزینه» در مقابل «سن» نیز به این صورت:

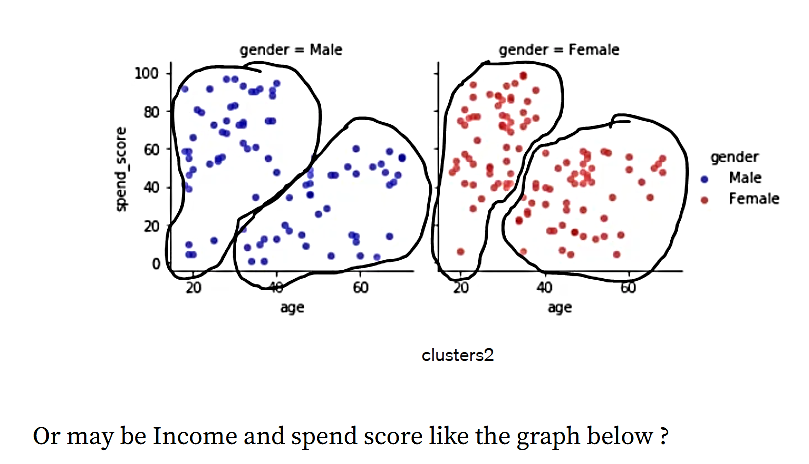
شکل 4. خوشه 2

یا ممکن است درآمد و امتیاز هزینه مانند نمودار زیر باشد.

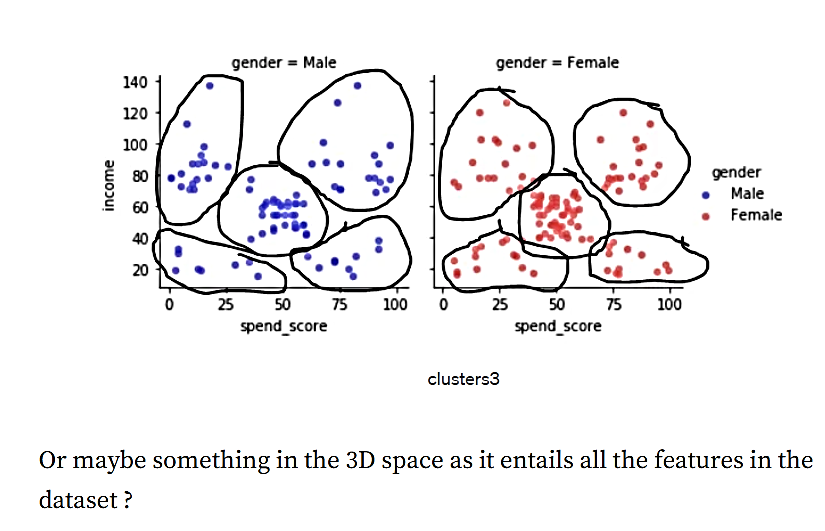
شکل 5. خوشه 3

یا می‌توان دسته‌بندی زیر را در فضای سه بعدی که شامل تمام ویژگیهای مجموعه داده است، ارائه نمود.

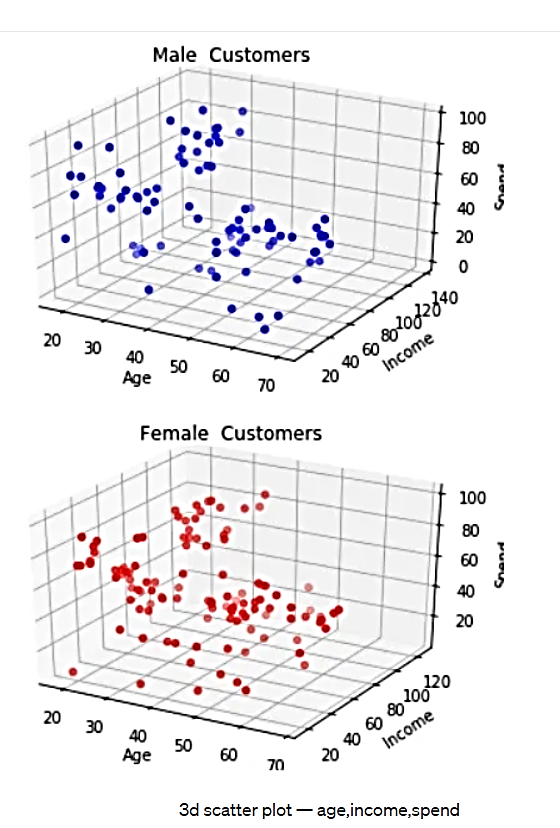
شکل 6. طرح پراکندگی سه‌ بعدی - سن، درآمد، هزینه

مشکل در انتخاب روش تقسیمبندی مناسب چیست؟

1. تیمهای بازاریابی ممکن است خوشه 3 را به خوشه 1 یا خوشه 2 ترجیح دهند؛ زیرا به نظر میرسد بهتر از هم جدا شدهاند.
2. بستگی دارد که ما واقعاً میخواهیم چند بخش داشته باشیم؟ بخشهای بیشتر به معنای نیاز به تولید محتوای بیشتر برای گروههای مختلف است.
3. بخشهای بسیار کم میتواند منجر به تعمیم بیش از حد شود.
4. Translation is too long to be saved

این مسائل، فقط با 4 ویژگی مشتری رخ داده است. در دنیای واقعی، صدها و هزاران رویداد، مشتری و دادههای خرید دارند. آنجا مسئله سختتر هم میشود. اجازه دهید بفهمیم که چگونه میتوانیم با استفاده از الگوریتمهای یادگیری ماشین به حل این موضوع بپردازیم. در ادامه به 3 رویکرد رایج توجه میکنیم و نتایج را با خوشههای برچسبگذاری شده توسط انسان مقایسه خواهیم کرد:

• خوشهبندی K -میانگین
• خوشهبندی سلسلهمراتبی 
• خوشهبندی DBSCAN

خوشهبندی K -میانگین

اینکه ماشین‌ها چگونه می‌آموزند چه چیزی بهترین است، از طریق به حداقل رساندن یک تابع ضرر انجام می‌شود. الگوریتم K Means به طور خاص مجموع مجذور فواصل را در نظر می‌گیرد. در این وبلاگ میتوانید توضیحات الگوریتم K Means را ببینید. تابع ضرر برای K Means به شرح زیر است:

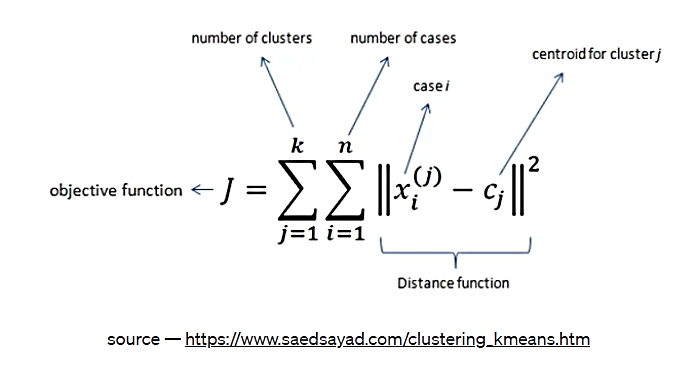
شکل 7. تابع ضرر الگوریتم K Means 

منبع:  https://www.saedsayad.com/clustering_kmeans.htm

ترجمه تصویر:

این تابع ضرر، اساساً میگوید که "مرکزهای خوشهای را برای من پیدا کن (برای k خوشه)  به گونهای که فاصله درون خوشهای در یک خوشه، برای همه خوشهها به حداقل برسد." این کار، اساساً یک مسئله بهینهسازی ریاضی است - فرمول حداقلسازی. مرکزهای خوشه‌ای نیز نوعی نقطه مرکزی در خوشه هستند. هنگامی که k مرکز خوشه پیدا شد، هر نقطه را میتوان به نزدیکترین مرکز آن اختصاص داد و نقاط دارای مرکز یکسان، هر خوشه را تشکیل میدهند.

حل معادله بالا ، یک مسئله NP-Hard است - به این معنی که حل آن در حوزه ریاضیات بسیار مشکل می‌باشد. از این رو برای حل این مسئله، از الگوریتمهای تقریب استفاده میکنیم. به عنوان مثال، الگوریتم Lyod به عنوان یک راه حل برای این مسئله، در تصویر زیر مشاهده می‌شود.

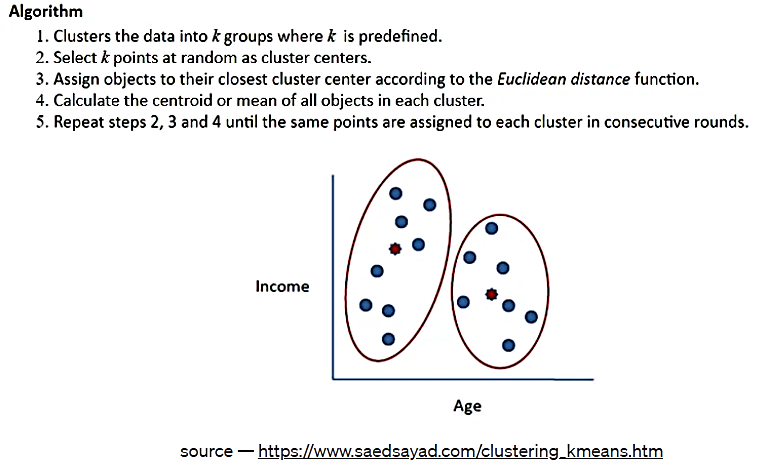
شکل 8. الگوریتم Lyod، منبع:  https://www.saedsayad.com/clustering_kmeans.htm

حساسیت راه‌اندازی، یکی از مسائلی است که در الگوریتمK -میانگین با آن مواجه می‌شویم و به این معنی است که خوشه‌های نهایی به دست آمده، به نحوه انتخاب مرحله ۲ در الگوریتم بستگی دارد. از این رو، لازم است که چندین تکرار از این الگوریتم را با مقداردهی اولیه متفاوت انجام دهیم و بررسی کنیم که کدام مقداردهی اولیه، با نیاز ما از خوشه‌ها مطابقت دارد. روش دیگر رسیدگی به این موضوع، استفاده از الگوریتم K -میانگین++  است. این الگوریتم مرکزهای خوشهای را در مرحله راهاندازی، با اختصاص دادن مرکزهای خوشهایِ تا حد امکان دور از یکدیگر (با به حداکثر رساندن فاصله بین خوشهای) تعیین میکند. برای کاهش تأثیر عوامل پرت، از یک الگوریتم احتمالی استفاده میشود. برخی از محدودیتهای الگوریتم K –میانگین عبارتند از:

 (منبع: www.appliedaicourse.com)

1. اندازههای مختلف خوشه، زمانی که  خوشهها به هم نزدیکتر هستند.

2. متفاوت بودن تراکم خوشهها

3. اَشکال غیر محدب

4. عدم استحکام نسبت به موارد پرت

(این مسائل بالا را می توان با استفاده از  تعریف تعداد خوشههای بیشتر و سپس گروه‌بندی زیرخوشهها، به صورت تاکتیکی حل کرد)

یکی دیگر از مسائل مربوط بهK -میانگین، تفسیرپذیری مرکز خوشه به دست آمده می‌باشد. مرکز یک خوشه ممکن است لزوماً یکی از نقاط داده نباشد، زیرا حاصل میانگین نقاط داده خوشه است. در مسائل واقعی، تیم‌های تجاری معمولاً تمایل دارند که مرکز خوشه یکی از نقاط داده باشد. بنابراین در این موارد، می‌توانیم از الگوریتم k-medoids استفاده کنیم. در اینجا به جای استفاده از centroid یا مرکز، از چیزی به نام medoid که یکی از نقاط داده است، استفاده میکنیم. به‌ جای محاسبه میانگین به‌عنوان مرکز، روی نقاط داده حرکت می‌کنیم تا medoidی را انتخاب کنیم که تابع ضرر ما را به بهترین نحو کاهش دهد. از این روش معمولاً برای تفسیرپذیرترکردن مدل‌ها استفاده می‌شود.

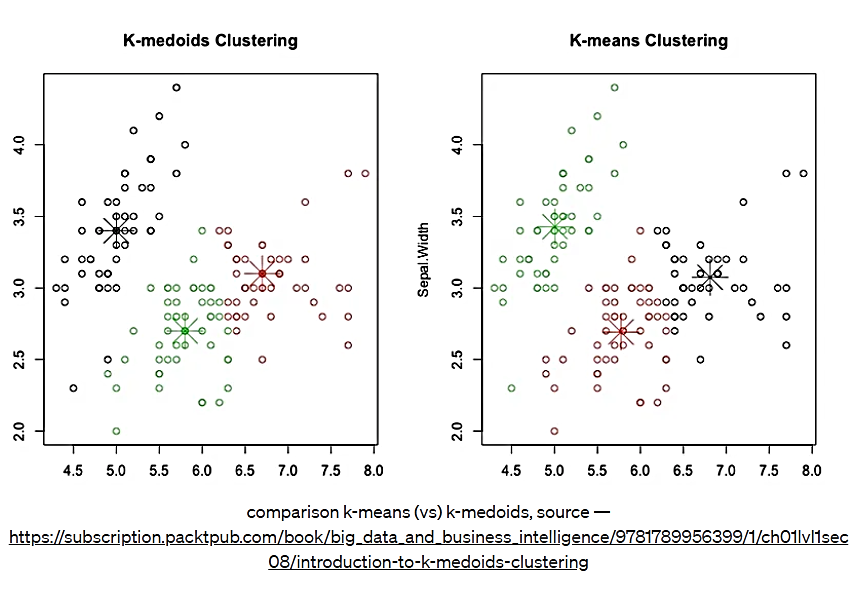
شکل 9. مقایسه دو الگوریتم K Means و K medoids

منبع: https://subscription.packtpub.com/book/big_data_and_business_intelligence/9781789956399/1/ch01lvl1sec08/introduction-to-k-medoids-clustering

همانطور که در شکل بالا میبینیم، K medoids، مرکزهای خوشهای را از میان نقاط داده انتخاب میکند در حالی که در K-میانگین، مرکز خوشه، یک نقطه داده نیست. انتخاب بهترین مقدار k، با استفاده از روش زانویی تابع ضرر انجام می‌شود. وقتی به مثال خود اعمال می‌کنیم، این را با جزئیات خواهیم دید.

پیچیدگی زمانی تابع K-میانگین از درجه  O(nkdi)می‌باشد که به ترتیب، تعداد نقاط (#pts)، تعداد دستهها (#clusters)، تعداد ویژگیها (#features) و تعداد دفعات تکرار الگوریتم (#iterations) است. در مواردی که k و i کوچک باشند، درجه سختی الگوریتم به صورت  O(nd) خواهد بود.

پیچیدگی فضایی تابع K-میانگین، O(nd+kd)  است که برای مقادیر کوچک میتوان آن را به O(nd) تقریب زد.

اجازه دهید K-میانگین را در python-sklearn برای مثال خود اعمال کنیم و نتایج را بررسی نماییم.

شکل 10. کد پایتون الگوریتم K-میانگین

ابتدا اطمینان حاصل میکنیم که ویژگیها، عددی و استاندارد شده هستند. سپس مقادیر k را از 2 تا 14 امتحان کرده و بهترین k  را با استفاده از روش Elbow  انتخاب میکنیم (مانند شکل زیر).

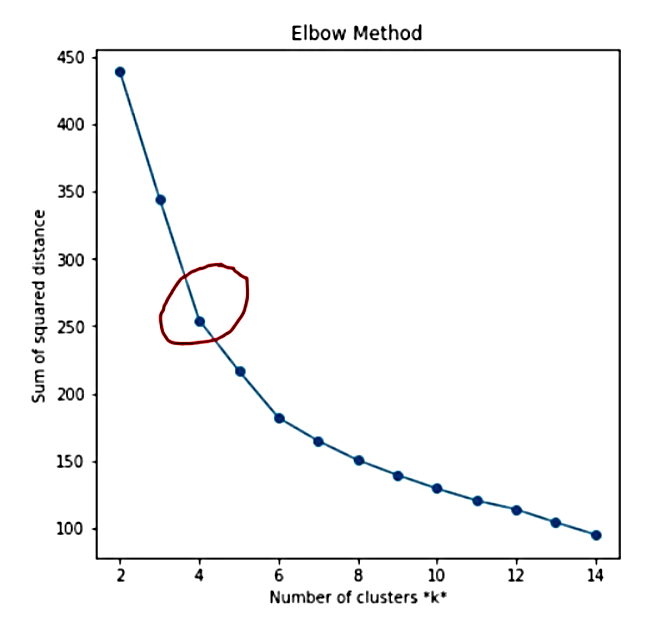
شکل 11. روش Elbow  ، k=4

بر اساس روش Elbow ، مشاهده می‌کنیم که تشکیل زانو از k=4 شروع می‌شود؛ پس می‌توانیم آن را به عنوان تعداد بهینه خوشه در K-میانگین نتخاب کنیم. می‌توانستیم از k=6 نیز استفاده کنیم، اما سعی می‌کنیم زیادهروی نکنیم چرا که ما فقط 200 نقطه داده داریم. حال اجازه دهید این خوشه ها را تجسم کنیم.

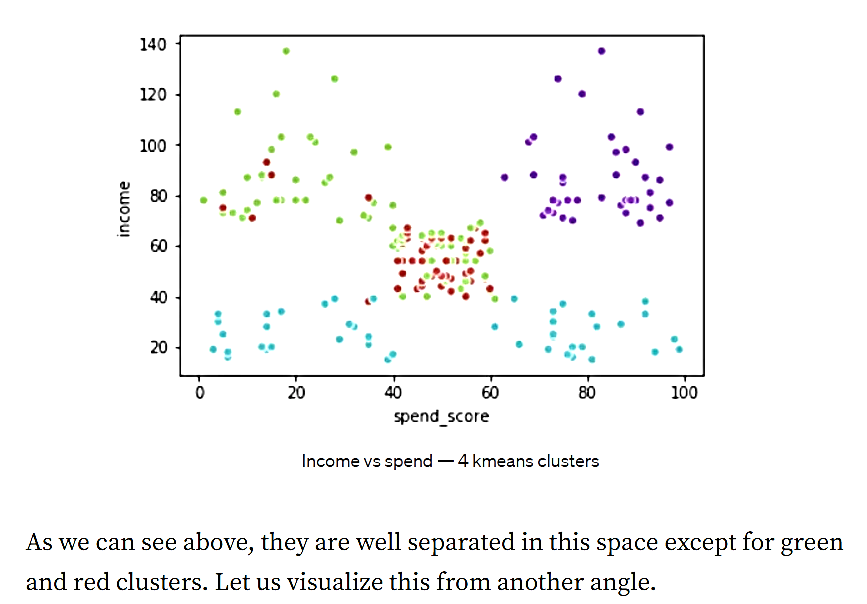
شکل 12. درآمد در مقابل هزینه- الگوریتم K-میانگین با 4 خوشه

همانطور که در بالا میبینیم، بهجز خوشههای سبز و قرمز، بقیه به خوبی از یکدیگر جدا شدهاند. اجازه دهید این را از زاویهای دیگر تجسم کنیم.

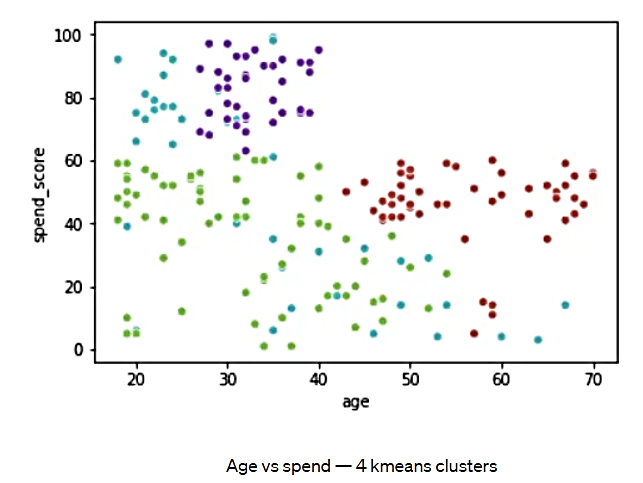
شکل 13. سن در مقابل هزینه- الگوریتم K-میانگین با 4 خوشه

بنابر این شکل، خوشههای قرمز برای گروههای سنی بالاتر هستند و خوشههای سبز برای گروههای سنی پایینتر. همچنین در ادامه نمودار پراکندگی سه بعدی را در طول ویژگیهای سن، درآمد، هزینه مشاهده می‎کنیم:

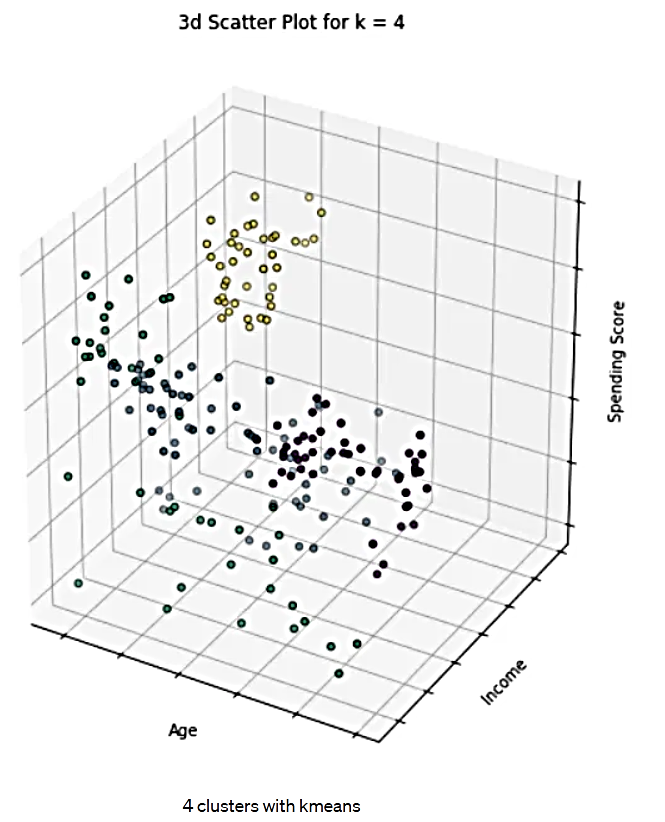
شکل 14. 4 خوشه در الگوریتم K-میانگین

خوشهبندی سلسلهمراتبی

الگوریتم سلسلهمراتبی دارای دو نوع تجمیعی و تقسیمکننده است که نوع تجمیعی، پرکاربردتر می‌باشد. این الگوریتم نقاط/خوشههای مشابه را به شیوهای سلسلهمراتبی گروه‌بندی میکند.

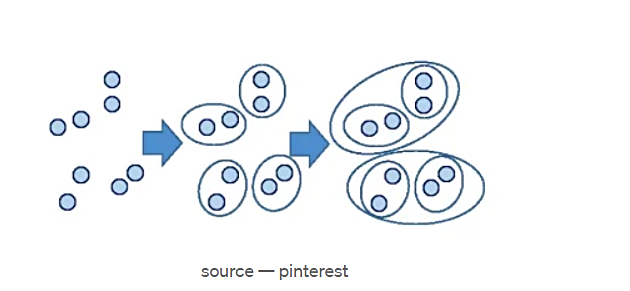
شکل 15. الگوریتم خوشهبندی سلسلهمراتبی

همانطور که در شکل بالا میبینیم، ابتدا همه نقاط را به عنوان خوشههای منفرد در نظر میگیرد و سپس در هر تکرار بعدی، نقاط مجاور را به خوشهها گروهبندی میکند و این روند گروهبندی نقاط/خوشهها به خوشهها را تکرار میکند تا زمانی که به یک خوشه بزرگ برسد. ما میتوانیم این رویکرد را در الگوریتم زیر مشاهده کنیم –

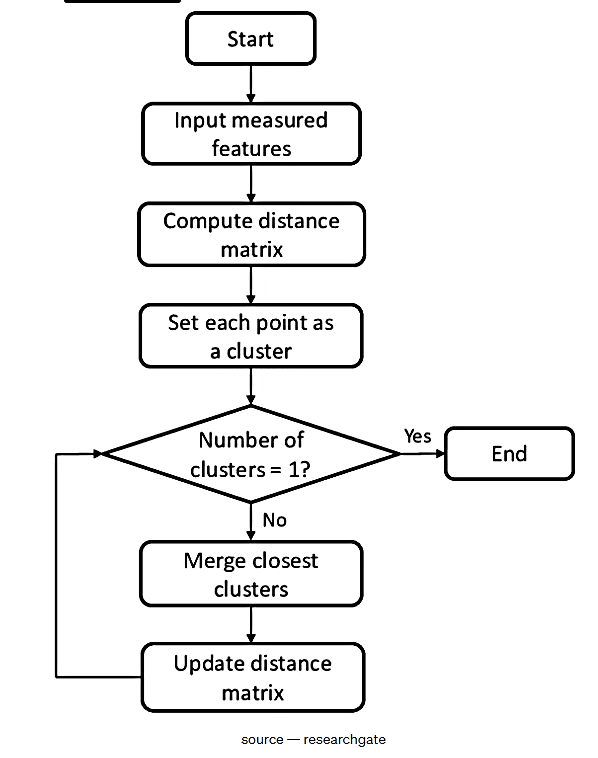
شکل 16. الگوریتم خوشهبندی سلسلهمراتبی

ترجمه تصویر:

یکی از ملاحظات عمده در خوشهبندی تجمیعی، انتخاب معیار مجاورت است. (یعنی - چگونه فاصله بین خوشهای را بین خوشهها و/یا نقاط تعریف کنیم). اجازه دهید به برخی از معیارهای مجاورت نگاه کنیم:

1. MIN : حداقل فاصله ممکن بین دو جفت خوشه را در نظر می‌گیرد که کوچکترین است. به عنوان مزیت اصلی می‌توان به این اشاره کرد که قادر است خوشههای غیر محدب شکل را نیز اداره کند. با این حال، به نقاط پرت حساس است؛ زیرا از حداقل فاصله بین خوشهها استفاده میکند.

2. MAX: شبیه min است اما به جای کمترین فاصله، بیشترین را در نظر میگیرد. این روش نسبت به نقاط پرت و نویز در خوشه بندی مقاومتر است. با این حال، امکان دارد در مواردی که خوشه‌هایی با اندازه ناهموار داریم، بد عمل کند.

3. میانگین گروه: میانگین ترکیب تمام نقاط را در هر دو جفت خوشه در نظر میگیرد. میتوانی از معیارهای فاصله مثل اقلیدسی، منهتن و... استفاده نمود.

4. فاصله بین مراکز

در حالت ایده‌آل، می‌توان هر یک از روش‌های بالا را تکرار کرد و آنچه را که برای مسأله موردنظر، بهترین کارایی را دارد انتخاب نمود.

پیچیدگی فضایی برای خوشه‌بندی تجمیعی، O(n²) است - که وقتی n بزرگ باشد، بزرگ خواهد بود و پیچیدگی زمانی نیز O(n³) می‌باشد. این پیچیدگیهای بسیار زیاد یکی از اشکالات عمده در استفاده از خوشهبندی تجمیعی هستند.

اجازه دهید خوشه‌بندی تجمیعی را در مثال خود اعمال کرده و آن را بررسی کنیم؛ مانند آنچه برایK -میانگین انجام دادیم، تعداد خوشه‌ها را 4 در نظر می‌گیریم.

شکل 17. کد پایتون الگوریتم خوشهبندی تجمیعی

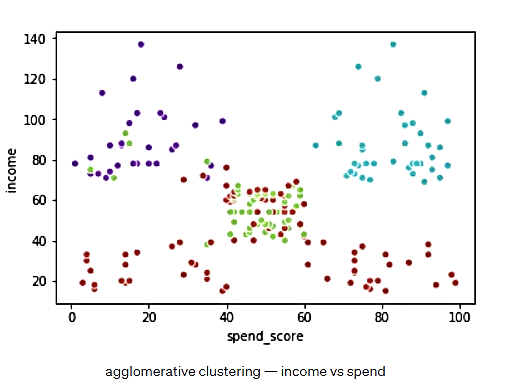
شکل 18. درآمد در مقابل هزینه- الگوریتم تجمیعی با 4 خوشه

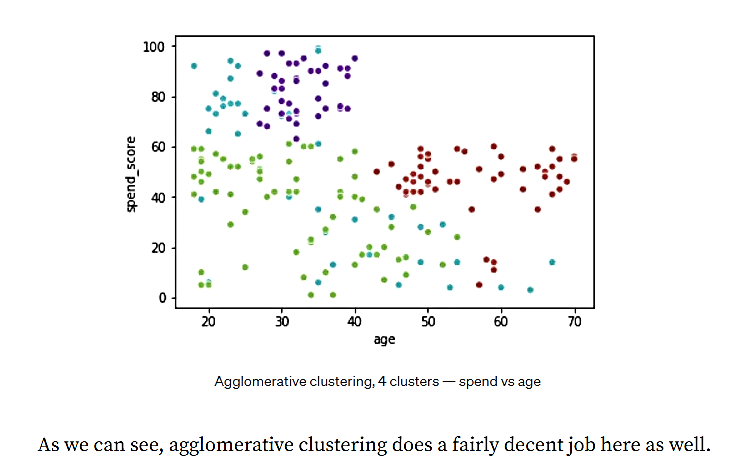
شکل 19. سن در مقابل هزینه- الگوریتم تجمیعی با 4 خوشه

همانطور که میبینیم، خوشهبندی تجمیعی، در اینجا نیز کار نسبتا مناسبی انجام میدهد.

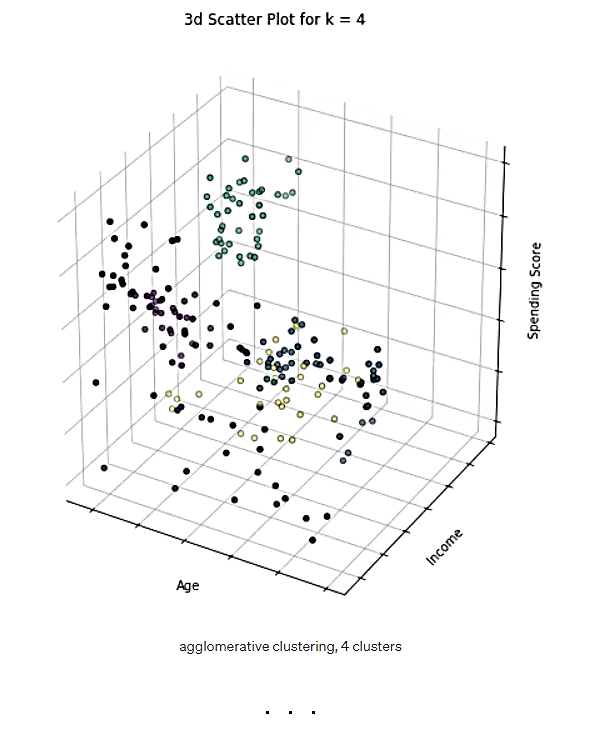
شکل 20. 4 خوشه در الگوریتم تجمیعی

خوشهبندی DBSCAN

DBSCAN سرواژه عبارت «Density based Spatial Clustering of applications of Noise» و به معنی خوشهبندی فضایی مبتنی بر چگالی کاربردهای نویز می‌باشد. اساس کار این نوع خوشه‌بندی به صورت زیر است:

هر نقطه را به یکی از 3 دسته زیر طبقه‌بندی میکند:

• نقطه مرکزی (اگر دارای حداقل امتیاز در اطراف شعاع اپسیلون خود باشد)
• نقطه مرزی (نقطه اصلی نیست اما دارای یک نقطه مرکزی در مجاورت اپسیلون است)
• نقطه نویز (همه نقاط دیگری که هسته و نقاط مرزی نیستند)

این تخصیص بر اساس 2 هایپرپارامتر انجام میشود:

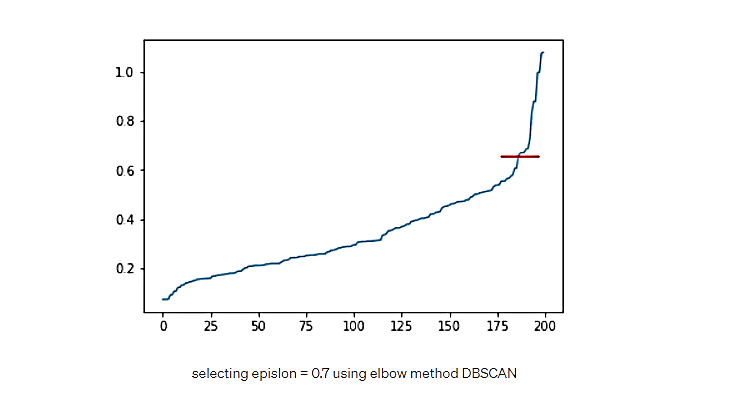
• اپسیلون (شعاع اطراف یک نقطه): اپسیلون با استفاده از روش Elbow، از طریق رسم فاصله هر نقطه از نزدیکترین همسایه x که در آنx  همان نقطه کمینه است، تعیین میشود.
• نقاط کمینه یا  min point (نقاط حداقل در اطراف نقطه مرکزی برای طبقه‌بندی آن به عنوان نقطه مرکزی/منطقه متراکم) که به عنوان معیارهای برای تعیین تراکم عمل می‌کند - می‌توان با استفاده از یک قانون سرانگشتی 2*d را در نظر گرفت که در آن d، ابعاد دادههاست.

در مرحله بعد، نقاط نویز را حذف میکند و روی هر نقطه مرکزی تکرار میشود، تا آن را به خوشهای شامل تمام نقاط متصل به نقطه مرکزی (به طور متراکم) اختصاص دهد. برای نقاط مرزی، آن نقطه به خوشه نقطه مرکزی، تعلق دارد. مراحل الگوریتم به شرح زیر می‌باشد.

شکل 21. الگوریتم خوشهبندی DBSCAN، منبع: wikipedia DBSCAN

بزرگترین مزیت DBSCAN توانایی آن در مدیریت نویز و استحکام آن در برابر نقاط دورافتاده، توانایی مدیریت خوشههای با شکل پیچیده و... است. با این حال، اگر دادهها دارای چگالی متغیر در فضا باشند، الگوریتم خوب عمل نمیکند. همچنین در دادههای با بُعد بالا و حساس نسبت به هایپرپارامترها نیز شکست میخورد.

پیچیدگی زمانی الگوریتم، (nlogn) و پیچیدگی فضایی آن، O(n) است. در حالتی که d بسیار کوچکتر از n باشد که در مقایسه با خوشه‌بندی تجمیعی، پیچیدگی خوبی به نظر می‌رسد.

شکل 22. کد پایتون الگوریتم خوشهبندی DBSCAN

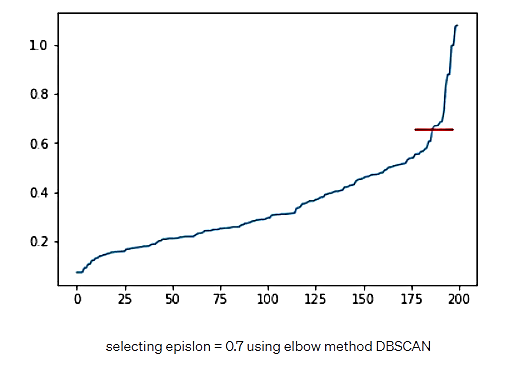
شکل 23. انتخاب اپسیلون به مقدار 0.7 با روش Elbow

الگوریتم DBSCAN، 6 خوشه تشکیل میدهد که برای مثال ما، کمی بیش از حد مناسب است. اجازه دهید تجسم دادهها را ببینیم:

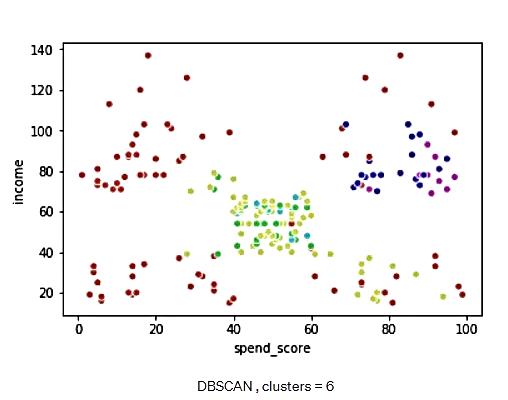
شکل 24. الگوریتم DBSCAN با 6 خوشه

مقایسه نتایج و جمعبندی

مقایسه برچسبگذاری انسان و الگوریتم K -میانگین

همانطور که در نمودارهای زیر میبینیم، الگوریتم K -میانگین، مانند انسان 4 خوشه را انتخاب میکند، اما این خوشهبندی، مقداری همپوشانی در نمودار درآمد در مقابل هزینه ایجاد میکند که برای انسان اینگونه نیست. اما اگر از منظر ویژگیهای هزینه در مقابل سن نگاه کنید، به نظر میرسد این جدایی، موجه می‌باشد. این خوشه‌بندیK -میانگین دارای مزیتی است که می‌تواند به داده‌های چند^[a] بعدی نگاه کند و بهترین تصمیم را برای خوشه‌بندی اتخاد نماید. کاری که ممکن است برای یک انسان دشوار باشد.

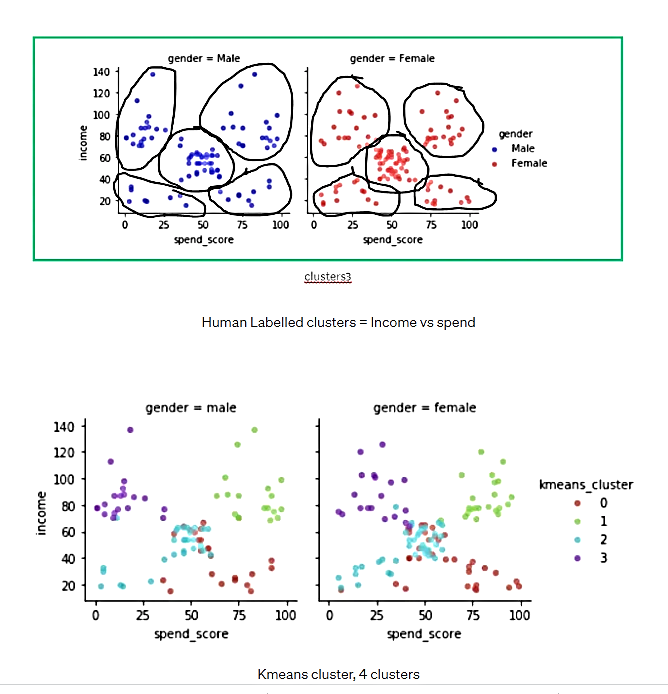
شکل 25. خوشههای ایجاد شده توسط انسان- درآمد در مقابل هزینه

شکل 26. خوشهبندی K -میانگین - 4 خوشه- درآمد در مقابل هزینه

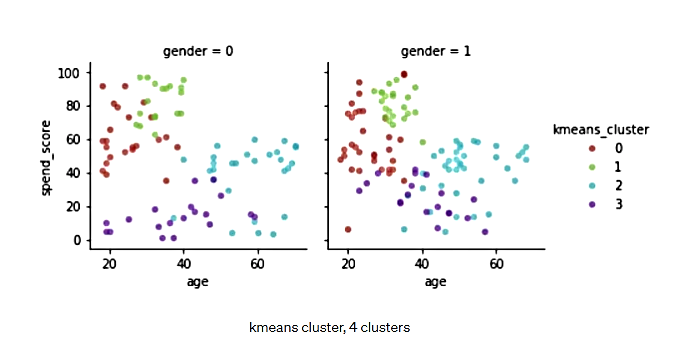
شکل 27. خوشهبندی K -میانگین - 4 خوشه- سن در مقابل هزینه

سایر معیارها برای انتخاب بهترین تعداد خوشه - شاخص Dunn، امتیاز Shiloutte

می‌توان از معیارDunn  که یک معیار نسبی است، برای تعیین خوشهها استفاده نمود. اگر مقدار این معیار بالا باشد، یعنی خوشهبندی بسیار خوب انجام شده؛ به این دلیل که فاصله بین خوشهای زیاد است و این همان چیزی است که ما میخواهیم. همچنین قطر خوشه کم می‌باشد که یعنی تابع ضرر کم خواهد بود. معیارDunn  به صورت نسبت "حداقل فاصله بین خوشهای" به "حداکثر فاصله درون خوشهای" محاسبه میشود.

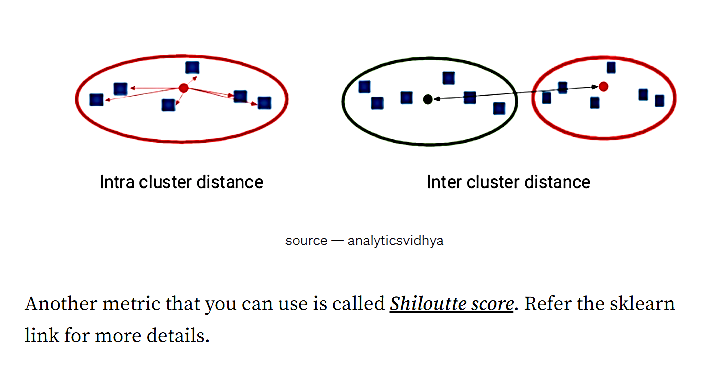
شکل 28. مقایسه فاصله درون خوشهای و بین خوشهای

معیار دیگری که می توان از آن استفاده نمود، امتیاز Shiloutte نام دارد. برای جزئیات بیشتر به این لینک مراجعه کنید.

سایر نتایج

• خوشهبندی سلسله مراتبی، تقریباً نتایج مشابهی با K -میانگین میدهد. در اینجا ما از پیوند ward به عنوان پارامتر مجاورت استفاده کردهایم. با این حال، می‌توانیم حداقل، حداکثر، میانگین گروهی و... را نیز آزمایش کرده و نتایج را با هم مقایسه نماییم. تنها عیب خوشه‌بندی تجمیعی این است که زمان اجرای بیشتری در مقایسه با K -میانگین دارد و همچنین انتخاب «تعداد خوشه‌ها» بر اساس ذهنیت و شناخت قبلی، برخلاف K -میانگین که از روش Elbow استفاده می‌کند، بسیار شهودی خواهد بود.
• DBSCAN در مثال ما با انتخاب 6 خوشه، کمی بیش از حد مناسب عمل کرد، اما همانطور که در بالا دیدیم، این الگوریتم نسبت به تغییرات جزئی در هایپرپارامتر بسیار حساس است. شما میتوانید با هایپر پارامترهای مختلف اپسیلون و  نقاط کمینه آزمایش انجام دهید و ببینید که کدام یک در این مثال، بهتر عمل میکند.
• در خوشه‌بندی هیچ پاسخ درست یا غلطی وجود ندارد. برخلاف وظایف طبقه‌بندی/رگرسیون که می‌توان عملکرد مدل را اندازه‌گیری کرد. در اینجا، چالش، انتخاب بهترین استراتژی خوشهبندی با توجه به الزامات کسبوکار است.
• می‌توانید شاخص‌های Dunn  و Shiloutte را آزمایش کنید و معیار مناسب خود را با توجه به نیازهای تجاریتان تعیین نمایید.