رگرسیون خطی - قسمت اول

رگرسیون
در بسیاری از مسائل، به دنبال ارتباط بین یک یا مجموعهای از متغیرها(مستقل) با یک متغیر هدف(وابسته) هستیم. در واقع میخواهیم بدانیم که بالا و پایین رفتن مقدار متغیرهای مستقل، چه تاثیری بر متغیر پاسخ یا هدف میگذارد.
توجه داشته باشید که این طیف مسائل با مسئلههای دستهبندی که در آنها به دنبال برچسبگذاری نمونهها هستیم متفاوت است. در واقع در مسائل دستهبندی، متغیر هدف گسسته است اما در مسائل رگرسیونی به دنبال یادگیری رفتار متغیر پاسخی هستیم که به صورت عددی و پیوسته مقدار میگیرد.
به عنوان مثال، هدف ما این است که یک مدل ایجاد کنیم که با استفاده از شاخصهای فیزیکی و سلامتی افراد، قادر باشد طول عمر آنها را پیشبینی کند. یا مدلی را تصور کنید که با داشتن مقدار قند خون و سطح بعضی آنزیمها در بدن افراد، فشارخون آنها را تخمین بزند. یا پیشبینی شاخص بورس اوراق بهادار و قیمت طلا براساس شاخصهای اقتصادی بازار. با توجه به مثالهایی که ذکر شد میتوان طیفی از مسائل مشابه را در دنیای اقتصاد، مهندسی، و ... معرفی و مدلسازی کرد.
در مدل رگرسیونی تلاش میشود تا ارتباط بین متغیرهای مستقل و وابسته به صورت یک الگوی شناختهشده بیان شود. در سادهترین حالت این ارتباط خطی در نظر گرفته میشود. یعنی در مثال بالا، در سادهترین حالت، میتوان فرض کرد که رابطه بین شاخصهای سلامتی افراد و عمر آنها از نوع خطی است، به این معنی که تغییرات در شاخصهای سلامتی باعث تغییرات خطی در عمر فرد میشود. اما البته، این رابطه میتواند پیچیدهتر نیز باشد و از مدلهایی با درجات بالاتر مانند سهمیها، ارتباطات لگاریتمی و غیره، استفاده کند. در شکل 1 ایدهی کلی مدلسازی رگرسیونی را مشاهده میکنید. نقاط قرمزرنگ دادههای واقعی را نشان میدهند و خطچین آبی، تخمینی است که مدل رگرسیونی از نحوهی رفتار دادهها به دست آورده است.
شکل 1: در مدلسازی رگرسیونی به دنبال بیان رفتار یک متغیر عددی هستیم.
به طور کلی رگرسیون یک تکنیک مدلسازی آماری است که به بررسی و مدلبندی ارتباط بین متغیرها میپردازد. سادهترین فرم رگرسیون، رگرسیون خطی است و در عین سادگی مزایای بسیار خوبی دارد. رگرسیون خطی به دلیل سادگی ذاتی خود، نیاز به محاسبات اندکی دارد و به راحتی قابل آموزش است و همچنین بنا بر اصل تیغ اوکام، باید سطح پیچیدگی مدل با سطح پیچیدگی مساله هماهنگ باشد. تیغ اوکام یک اصل فلسفی است که توسط ویلیام اوکام، فیلسوف قرن چهارده میلادی مطرح شد. این اصل بیان میکند که اگر دو تبیین و توضیح مختلف برای توجیه کردن یک پدیده وجود داشت، آن که سادهتر است، ارجحیت دارد. در دنیای یادگیری ماشین، از این اصل جهت انتخاب مدلهایی با سطوح پیچیدگی مختلف استفاده میشود. بنابراین اگر مجموعهی داده پیچیدگی پایینی دارد، بهتر است از مدل ساده استفاده شود. در کاربردهای عملی نیز در بسیاری موارد مجموعهی دادهها دارای پیچیدگی بالایی نیستند و مدلهای سادهتر مانند رگرسیون خطی میتوانند به خوبی از عهدهی حل مساله بربیایند. مزیت دیگر رگرسیون خطی پایه و اساسی بودن آن است. به این معنا که اگر این مدل به درستی درک شود، مدلهای رگرسیونی پیچیدهتر نیز به سادگی درک خواهند شد؛ زیرا آنها نیز با روشی مشابه تعریف میشوند.
متغیرها به صورت کلی دو دسته تقسیم میشوند:
1-متغیر پاسخ یا هدف (وابسته)
2-متغیر(های) مستقل، رگرسور، پیشبینیکننده، توضیحی
رگرسیون خطی
فرض کنید یک متغیر هدف وجود دارد و آن را با ![]() نمایش و یک متغیر پیشگو داریم و آن را با
نمایش و یک متغیر پیشگو داریم و آن را با ![]() نمایش میدهیم. اولین گام در تشخیص رابطه بین
نمایش میدهیم. اولین گام در تشخیص رابطه بین ![]() و
و ![]() در رگرسیون خطی ساده رسم نمودار پراکنش(پراکندگی) آنهاست. نمودار پراکنش، پراکندگی دو متغیر در برابر یکدیگر را نمایش میدهد. اگر در نمودار پراکنش بین
در رگرسیون خطی ساده رسم نمودار پراکنش(پراکندگی) آنهاست. نمودار پراکنش، پراکندگی دو متغیر در برابر یکدیگر را نمایش میدهد. اگر در نمودار پراکنش بین ![]() و
و ![]() ، یک روند خطی دیده شود؛ یعنی در نمودار رسم شده، ارتباط بین این دو متغیر به کمک یک خط فرضی با شیب مثبت یا منفی قابل بیان باشد، میتوانیم بگوییم که رگرسیون خطی یک راهحل مناسب برای این مساله است.
، یک روند خطی دیده شود؛ یعنی در نمودار رسم شده، ارتباط بین این دو متغیر به کمک یک خط فرضی با شیب مثبت یا منفی قابل بیان باشد، میتوانیم بگوییم که رگرسیون خطی یک راهحل مناسب برای این مساله است.
در رگرسیون خطی ارتباط بین متغیر وابسته ![]() و متغیر مستقل
و متغیر مستقل ![]() توسط یک معادلهی خطی بیان میشود:
توسط یک معادلهی خطی بیان میشود:
![]()
یعنی به شرط دانستن مقدار متغیر مستقل، متغیر هدف به صورت خطی تغییر میکند شیب و عرض از مبدا در اینجا نحوهی تغییر متغیر پاسخ را مشخص میکنند.![]() و
و ![]() ضرایب مدل رگرسیونی هستند که به ترتیب پارامترهای عرض از مبدا و شیب خط رگرسیونی را نمایش میدهند.
ضرایب مدل رگرسیونی هستند که به ترتیب پارامترهای عرض از مبدا و شیب خط رگرسیونی را نمایش میدهند.![]() نیز خطای مدل را نشان میدهد. خطای
نیز خطای مدل را نشان میدهد. خطای![]() به دلیل خطای اندازهگیری و یا در نظر نگرفتن سایر متغیرهای مستقل تاثیرگذار بر پاسخ به وجود میآید.
به دلیل خطای اندازهگیری و یا در نظر نگرفتن سایر متغیرهای مستقل تاثیرگذار بر پاسخ به وجود میآید.
هدف در رگرسیون خطی، این است که خطی به دادهها برازش داده شود که به بهترین نحو ارتباط بین متغیر پاسخ و متغیر مستقل را مشخص کند. به این منظور باید ![]() و
و ![]() که نشاندهندهی عرض از مبدا و شیب خط رگرسیونی هستند را برآورد کرد و خط رگرسیونی مناسب را بهدست آورد. در واقع در حل این مسائل به دنبال مناسبترین مقادیر برای پارامترهای شیب و عرض از مبدا خط رگرسیونی هستیم. در شکل 2 پراکندگی نمونههای داده و خط رگرسیونی برازش داده شده به آنها را مشاهده میکنید.
که نشاندهندهی عرض از مبدا و شیب خط رگرسیونی هستند را برآورد کرد و خط رگرسیونی مناسب را بهدست آورد. در واقع در حل این مسائل به دنبال مناسبترین مقادیر برای پارامترهای شیب و عرض از مبدا خط رگرسیونی هستیم. در شکل 2 پراکندگی نمونههای داده و خط رگرسیونی برازش داده شده به آنها را مشاهده میکنید.
شکل 2: مدل فرضی رگرسیون خطی
تخمین پارامترها
روشهای مختلفی برای برآورد ![]() و
و ![]() وجود دارند:
وجود دارند:
1-کمترین مربعات خطا : (LS) یک روش غیرپارامتری است که در آن، بر خلاف رگرسیون پارامتری، نیاز به فرض نرمال بودن توزیع متغیر وابسته به شرط دانستن مقدار متغیر پیشگو یا مستقل ندارد. در روش غیرپارامتری، از توزیعهای احتمالی برای مدلسازی متغیرها استفاده نمیشود.
2-حداکثر درستنمایی (ML): یک روش پارامتری است و به فرض نرمال بودن توزیع متغیر وابسته نیاز است.
در این مقاله پارامترها به کمک روش اول تخمین زده میشوند. روش دوم نیاز به کمی دانش فنی آماری دارد و به همین دلیل از ذکر آن صرف نظر میکنیم. البته، این دو روش بهطور کلی منجر به تخمینهایی سازگار با یکدیگر خواهند شد.
در صورت تخمین پارامترها معادله خط رگرسیونی برازش داده شده به دادهها به صورت زیر خواهدبود:
![]()
علامت کلاه بالای پارامترها و متغیر پاسخدهندهی این است که این مقادیر تخمین و پیشبینی شدهاند. منظور این است با استفاده از مجموعه دادهی آموزشی، پارامترهای مدل تخمین زدهمیشوند. سپس با استفاده از این پارامترهای تخمینی و مقادیر متغیرهای مستقل در مجموعه دادهی آزمایشی، مقدار متغیر وابستهی متناظر با آن پیشبینی خواهد شد.
معادلهی بالا برای تمام اعضای مجموعه داده برقرار است یعنی:
![]()
تفسیر هر کدام از پارامترها به صورت زیر است:
![]() : تخمین میزند که به ازای
: تخمین میزند که به ازای ![]() (درصورتی که مقدار
(درصورتی که مقدار ![]() در دامنه
در دامنه ![]() باشد)، متوسط مقدار متغیر پاسخ برابر با
باشد)، متوسط مقدار متغیر پاسخ برابر با ![]() است.
است.
![]() : تخمین میزند که به ازای یک واحد تغییر در متغیر مستقل، متوسط مقدار متغیر پاسخ به اندازه
: تخمین میزند که به ازای یک واحد تغییر در متغیر مستقل، متوسط مقدار متغیر پاسخ به اندازه ![]() تغییر میکند.
تغییر میکند.
فرضیات مدل رگرسیون خطی
مدل رگرسیون خطی نیز مانند هر الگوریتم دیگری دارای برخی پیشنیازها و فرضیات است. اگر فرضیات مدل برقرار بود، آنگاه میتوان به خروجیها و عملکرد مدل اطمینان کرد.
رگرسیون خطی بر اساس سه فرض اصلی مدلسازی میشود که عبارتند از:
- خطی بودن امید ریاضی شرطی متغیر وابسته به متغیرهای مستقل (خطی بودن مدل نسبت به پارامترهایش):
![]()
- ثبات واریانس شرطی متغیر وابسته:
![]()
- ناهمبستگی مقادیر متغیر وابسته بین نمونههای مختلف:
![]()
اگر با مفهوم امید ریاضی و واریانس آشنایی ندارید، توصیه میکنیم که فایل مربوط به نظریهی احتمال را از سری فایلهای مربوط به ریاضیات یادگیری ماشین مطالعه بفرمایید.
فرض اول در رگرسیون خطی بیان میکند که اگر مقدار متغیر پیشگو یا مستقل را بدانیم، میانگین مقدار متغیر وابسته یا پاسخ به صورت یک تابع خطی از متغیر پیشگو بیان میشود.
رابطهی دوم بیان میکند که اگر مقدار متغیر پیشگو را بدانیم، واریانس متغیر پاسخ برابر با یک مقدار ثابت خواهد بود.
فرض سوم بیان میکند که بین مقدار خطای اندازهگیری در بین نمونههای مختلف موجود در مجموعه داده، ارتباطی وجود ندارد.
برآورد پارامترها به روش حداقل مربعات خطا
در این روش ![]() ها طوری بدست میآیند که اختلاف
ها طوری بدست میآیند که اختلاف ![]() و
و ![]() تا آنجا که ممکن است کم باشد. یعنی در بین تمام خطوط راست موجود که برای بیان ارتباط بین دو متغیر استفاده میشوند، خطی را انتخاب میکنیم که مقدار میانگین جمع مجذور اختلاف بین مقادیر واقعی و مقادیر پیشبینی شده (خطا) در آن حداقل باشد.
تا آنجا که ممکن است کم باشد. یعنی در بین تمام خطوط راست موجود که برای بیان ارتباط بین دو متغیر استفاده میشوند، خطی را انتخاب میکنیم که مقدار میانگین جمع مجذور اختلاف بین مقادیر واقعی و مقادیر پیشبینی شده (خطا) در آن حداقل باشد.
تابع ![]() را به صورت زیر تعریف میکنیم:
را به صورت زیر تعریف میکنیم:
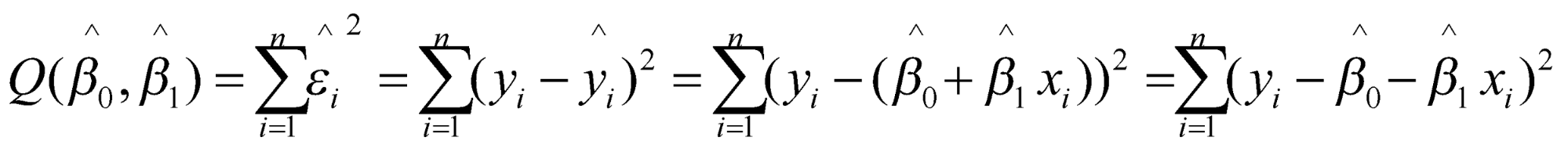
هدف مینیمم کردن معادله ![]() است. بنابراین باید نسبت به پارامترها مشتق گرفته و آنها را برابر صفر قراردهیم) اگر نیاز به مرور مفاهیم و روابط مربوط به مشتقگیری دارید، توصیه میکنیم به فایل حساب دیفرانسیل از مجموعه فایلهای ریاضیات یادگیری ماشین مراجعه کنید(:
است. بنابراین باید نسبت به پارامترها مشتق گرفته و آنها را برابر صفر قراردهیم) اگر نیاز به مرور مفاهیم و روابط مربوط به مشتقگیری دارید، توصیه میکنیم به فایل حساب دیفرانسیل از مجموعه فایلهای ریاضیات یادگیری ماشین مراجعه کنید(:
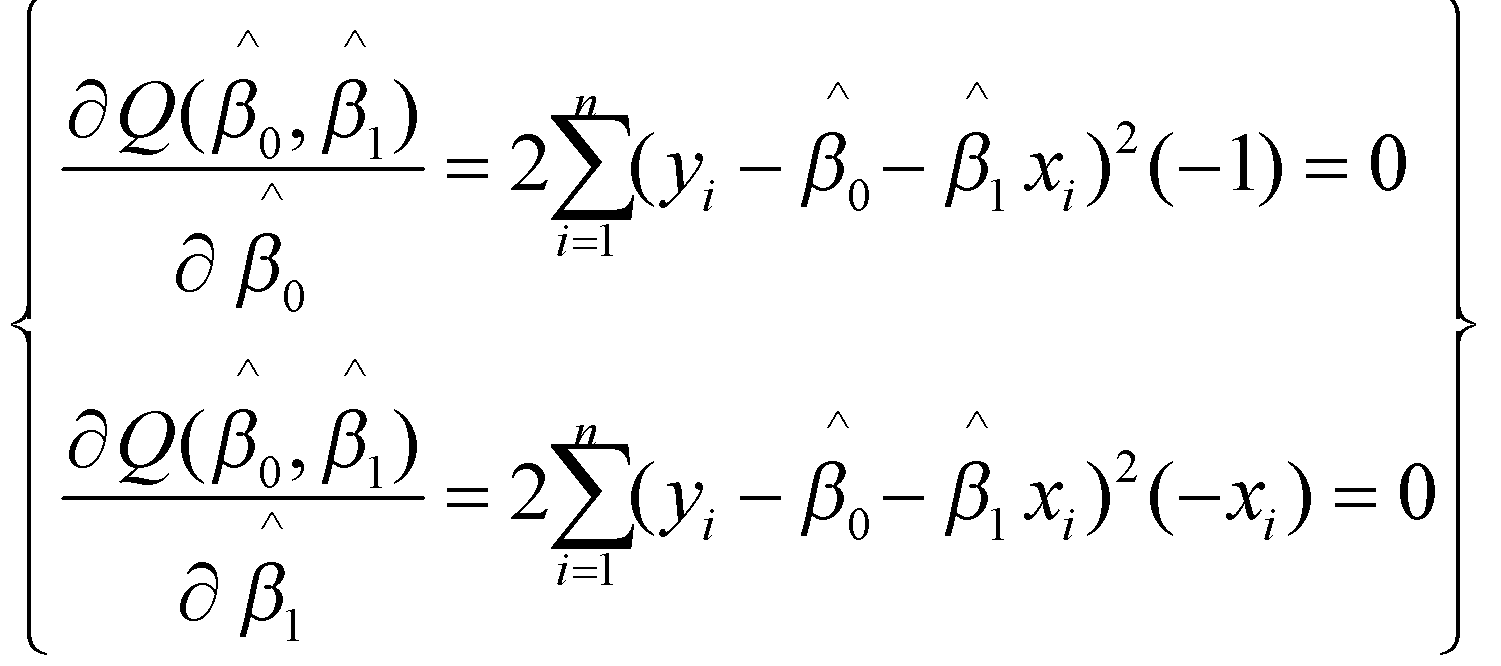
در نتیجه داریم:
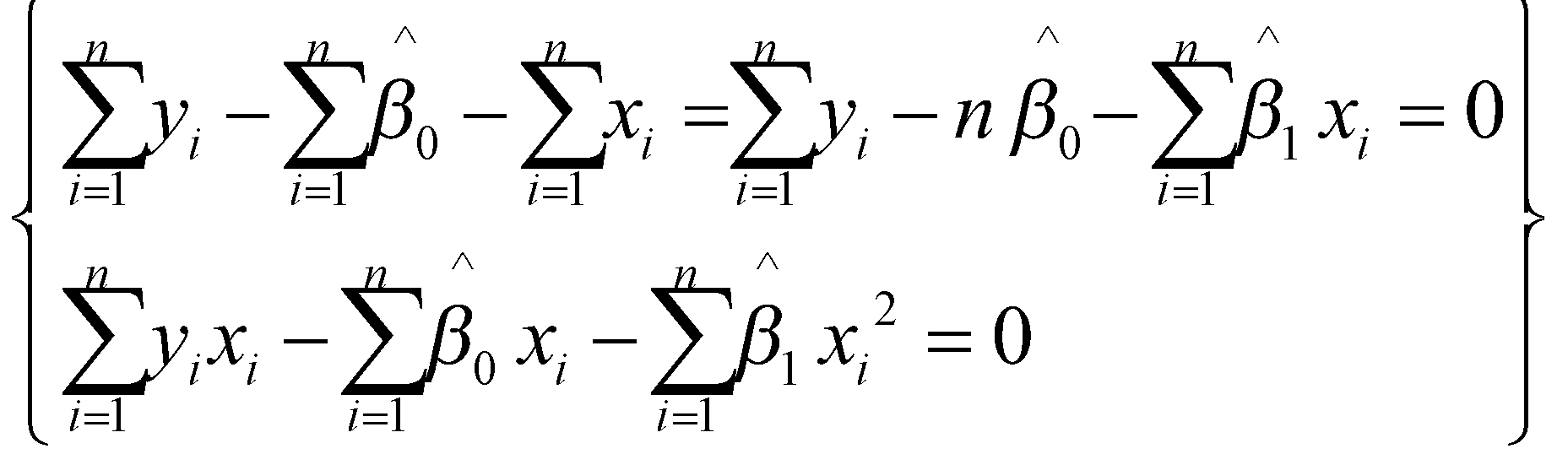
از معادلهی اول داریم:
![]()
با جایگذاری ![]() در معادلهی دوم داریم:
در معادلهی دوم داریم:
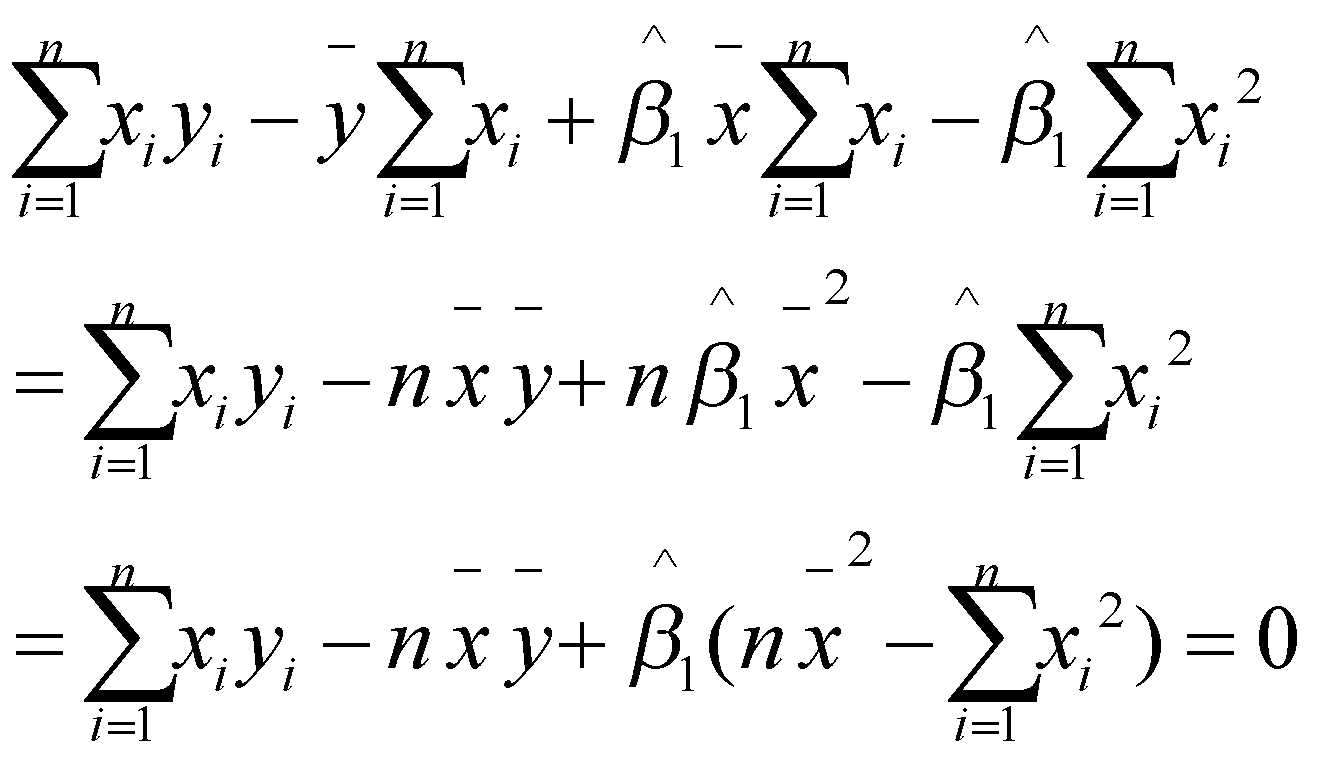
بنابراین ![]() به فرم زیر قابل نوشتن است:
به فرم زیر قابل نوشتن است:
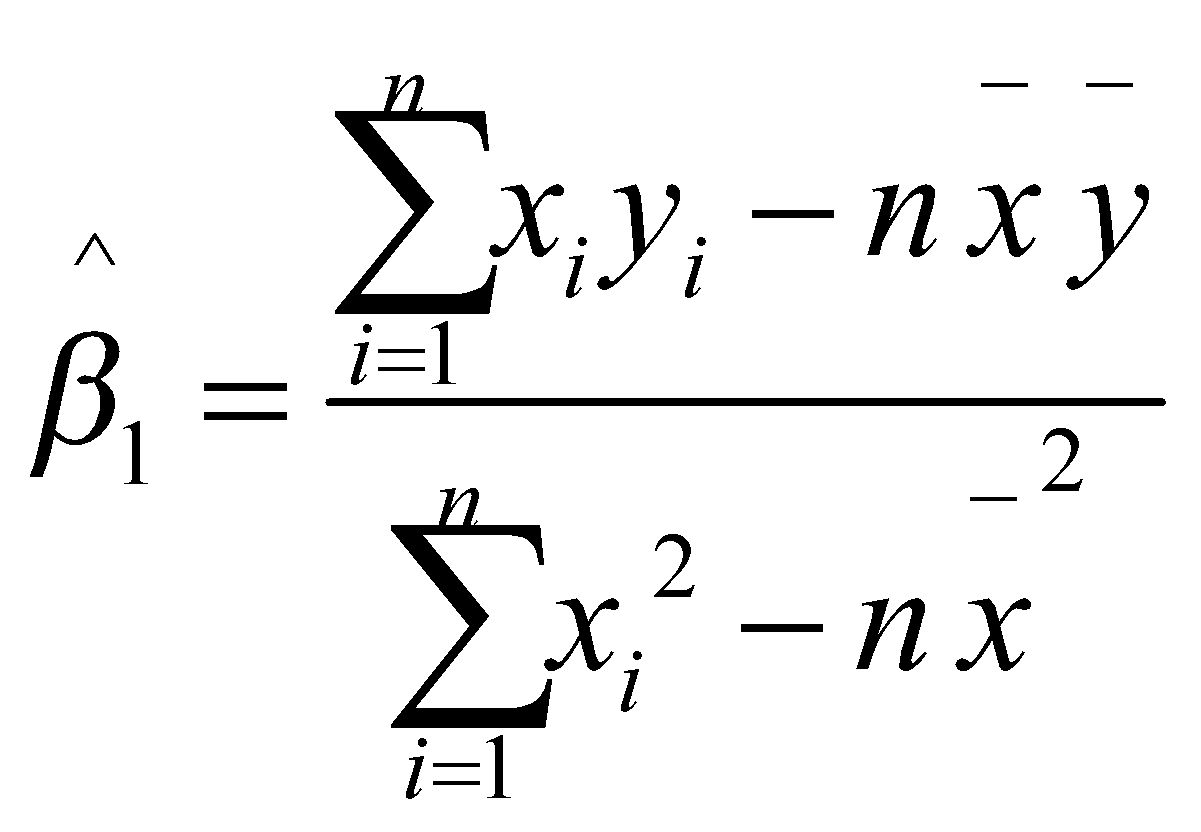
میتوان نشان داد که این تخمینها دارای ویژگیهای مطلوبی هستند. به عنوان مثال، میتوان گفت که این تخمینها ترکیبی خطی از مقادیر متغیرهای وابسته هستند. همچنین میتوان ثابت کرد که هر دوی آنها نااریب هستند و واریانسی با فرم بسته و مشخص دارند. اگر نمیدانید ترکیب خطی چیست، توصیه میکنیم که به فایل مربوط به جبر خطی از مجموعه فایلهای ریاضیات یادگیری ماشین مراجعه بفرمایید.
علاوه بر سه فرض اصلی که برای مدل رگرسیونی در بالا ذکر شد. یک فرض اختیاری نیز وجود دارد که اگر آن را بپذیریم، میتواند خواص مطلوبی به مدل رگرسیونی ببخشد.
اگر فرض کنیم که خطای اندازهگیری مدل دارای توزیع نرمال با میانگین 0 و واریانس ثابت ![]() است (اگر با توزیعهای احتمال، مخصوصا توزیع نرمال آشنایی ندارید، توصیه میکنیم که به فایل نظریهی احتمال مراجعه بفرمایید)یعنی:
است (اگر با توزیعهای احتمال، مخصوصا توزیع نرمال آشنایی ندارید، توصیه میکنیم که به فایل نظریهی احتمال مراجعه بفرمایید)یعنی:
![]()
میتوان نشان داد که از ترکیب این فرض با سه فرض قبلی نتیجهی زیر حاصل میشود:
![]()
یعنی با دانستن مقدار متغیر مستقل، توزیع متغیر پاسخ یا وابسته توزیع نرمال با مشخصات بالا خواهد بود.
اگر بخواهیم برای پیداکردن تخمین پارامترها از روش حداکثر درستنمایی استفاده کنیم، لازم است که فرض چهارم را بپذیریم.
آزمون معناداری مدل رگرسیونی
در فایل نظریه احتمال به طور خلاصه به آزمون فرضها اشاره کردیم. هرگاه بخواهیم یک فرضیه را به صورت آماری و دقیق تست کنیم، به سراغ آزمون فرضها میرویم.
در مورد مدل رگرسیون خطی نیز میتوانیم فرضیههایی را مطرح کنیم. به عنوان مثال، میتواند سوال ما این باشد که آیا شیب خط رگرسیونی برابر با 0 است یا خیر. همانطور که میدانید، خط راست با شیب 0 به معنای یک خط افقی است . اگر شیب خط رگرسیونی برابر با 0 باشد، به این معنی است که با تغییر مقدار متغیر پیشگو، هیچ تغییری در مقدار متغیر پاسخ ایجاد نمیشود. در این حالت میتوانیم نتیجه بگیریم که متغیر پیشگو هیچ تاثیری بر روی متغیر پاسخ ندارد. یا به عنوان مثالی دیگر، سوال ما میتواند این باشد که آیا عرض از مبدا خط رگرسیونی برابر 0 است یا خیر.
برای تست کردن چنین فرضیههایی میتوانیم به سراغ آزمون فرضها برویم و از این طریق آنها را بررسی کنیم.
برای آزمون کردن فرضهایی که در بالا ذکر شد، دو نوع آزمون موجود است. در روش اول میتوانیم از آزمون تی استفاده کنیم که آمارهی آزمون آن از توزیع احتمال تی پیروی میکند. توزیع احتمال تی به طور مختصر در فایل نظریهی احتمال از مجموعه فایلهای ریاضیات پایه معرفی شده است.
به عنوان مثال آزمون 0 بودن شیب خط رگرسیونی را به صورت زیر بیان میکنیم:
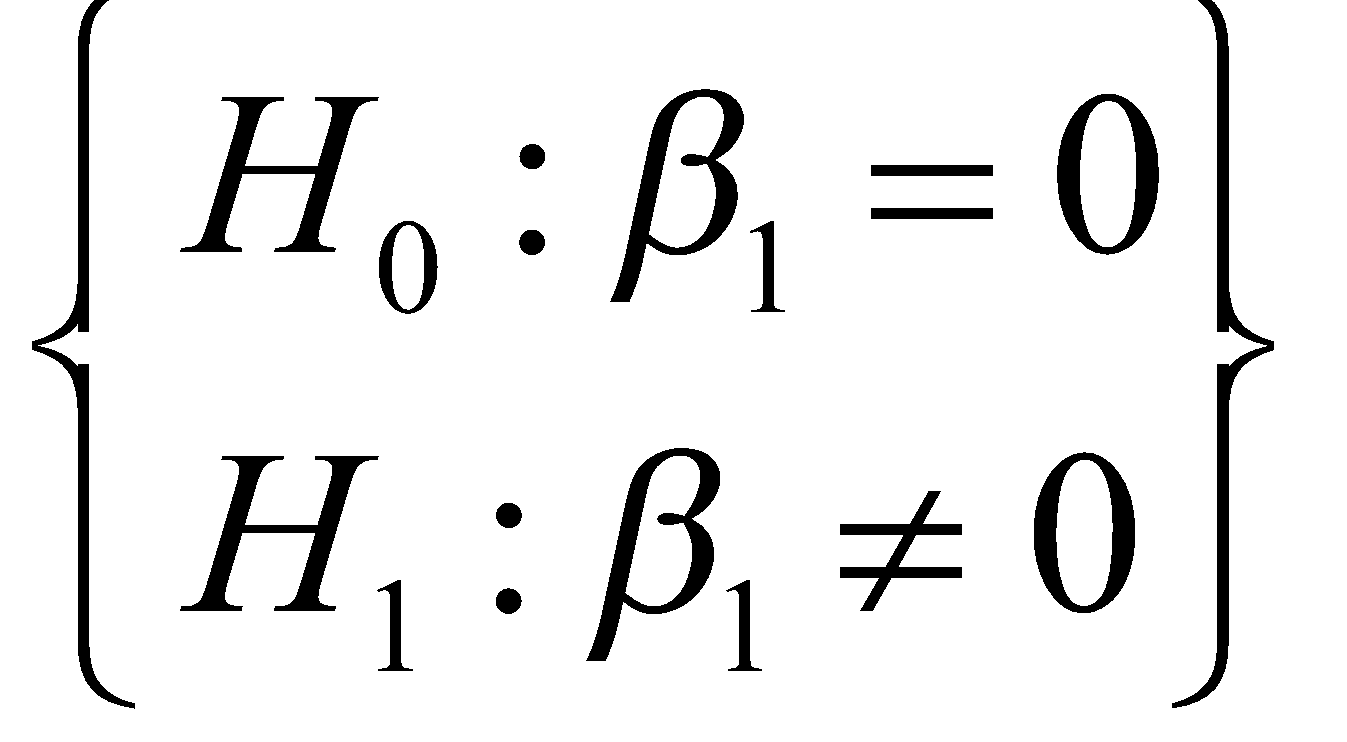
که در آن فرض اولیه این است که شیب خط رگرسیونی برابر 0 است؛ و فرض مقابل آن این است که شیب خط رگرسیونی هر مقداری به جز 0 دارد. شما میتوانید آزمون را به دلخواه خودتان تعریف کنید. آمارهی آزمون بالا به فرم زیر تعریف میشود:
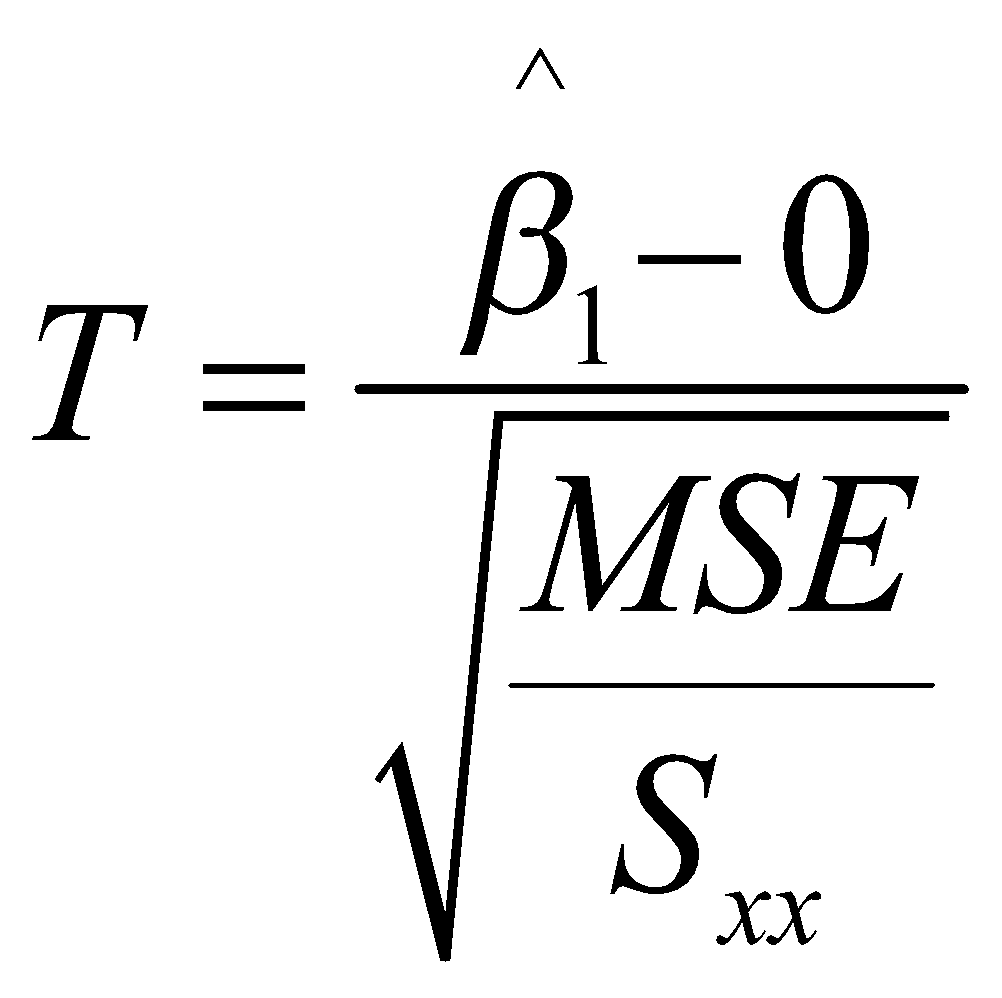
که در آن منظور از ![]() ، میانگین مربعات خطا است و
، میانگین مربعات خطا است و ![]() به صورت زیر تعریف میشود:
به صورت زیر تعریف میشود:
![]()
پس از به دست آوردن مقدار آمارهی آزمون، باید آن را با یک چندک از توزیعی که آمارهی آزمون از آن پیروی میکند مقایسه کنیم و نتیجهی این مقایسه، نتیجهی آزمون را مشخص میکند. منظور از چندک توزیع، نقطهای از توزیع احتمال است که مقدار معین از چگالی احتمال در نقاط قبل از آن ذخیره شده است. به عنوان مثال در شکل ۳ تابع چگالی احتمال طول مجموعهای از ماهیها نمایش داده شده است. طول آنها از توزیع نرمال با میانگین ۱۶ و انحراف معیار ۴ پیروی میکند. حال سوال پرسیده شده است که "چه طولی از ماهیها است که 10 درصد ماهیها حداکثر آن مقدار طول را دارا هستند؟". بنابراین باید نقطهای را بیابیم که انتگرال پشت آن برابر با 0.1 بشود. به آن نقطه چندک 0.1 توزیع میگوییم. معیار انتخاب چندکی از توزیع که برای مقایسه با مقدار آمارهی آزمون انتخاب میشود، سطح اطمینان مورد نظر در آزمون است.
شکل 3: نمایش چندک یک دهم یک توزیع نرمال
در اینجا لازم است تا ابتدا دربارهی مفهوم خطای نوع اول و دوم صحبت کوتاهی داشته باشیم.
به طور کلی آزمون فرض آماری به دو صورت میتواند دچار خطا شود. در آمار، اگر فرض اولیهی آزمون صحیح باشد اما آزمون به غلط آن را رد کند، میگوییم آزمون دچار خطای نوع اول شدهاست. در حالت برعکس، اگر فرض مقابل صحیح باشد و آزمون به غلط فرض اولیه را بپذیرد، میگوییم آزمون دچار خطای نوع دوم شدهاست.
هنگامی که آمارهی آزمون را براساس نمونهی مشاهدهشده محاسبه میکنیم، باید سطح خطای مورد نظر خود را نیز مشخص کنیم. به صورت قراردادی، سطح خطای مورد نظر معمولاً براساس خطای نوع اول بیان میشود.
اگر در نظر بگیریم که آزمون حداکثر 5% اوقات خطای نوع اول داشته باشد، یعنی آزمون با سطح اطمینان حداقل 95% انجام میشود.
به صورت قرارادادی احتمال خطای نوع اول را با ![]() و احتمال خطای نوع دوم را با
و احتمال خطای نوع دوم را با ![]() نمایش میدهند.
نمایش میدهند.
حالا که مفهوم و نمادگذاری مربوط به خطاهای نوع اول و دوم را میدانید، میتوانید عبارت زیر را درک کنید:
![]()
پس از محاسبهی مقدار آمارهی آزمون، قدرمطلق آن را با چندک![]() از توزیع تی با
از توزیع تی با ![]() درجهی آزادی مقایسه میکنیم. در اینجا منظور از
درجهی آزادی مقایسه میکنیم. در اینجا منظور از ![]() تعداد نمونههای موجود در مجموعه دادهی آموزشی است.
تعداد نمونههای موجود در مجموعه دادهی آموزشی است.
درجهی آزادی یک مفهوم آماری است و بیانگر تعداد متغیرهایی است که در یک شرایط خاص میتوانند آزادانه مقدار بگیرند. بیشتر از این لازم نیست که در اینجا در مفهوم درجهی آزادی عمیق شویم. میتوان درجهی آزادی را مانند یکی از پارامترهای مدل در نظر گرفت که در آزمون تی برابر دو واحد کمتر از تعداد نمونههای موجود در مجموعه دادهی آموزشی است.
لازم نیست که نگران باشید، این محاسبات در پایتون میتوانند به کمک کتابخانههای موجود به صورت اتوماتیک انجام شوند و شما نتیجهی تست را مشاهده کنید.
به روش دوم انجام این کار، تجزیهی واریانس (ANOVA) میگوییم. ایدهی کلی این روش بر اساس تجزیه پراکندگی ذاتی متغیر پاسخ است.
متغیر وابسته یا پاسخ، به عنوان یک متغیر تصادفی دارای یک واریانس مشخص در نمونهی تصادفی است. میدانیم هر مدلی که در دنیای یادگیری ماشین وجود دارد دارای خطا است و هیچ مدلی بینقص نیست. ایده تجزیه واریانس این است که مدل بخشی از پراکندگی ذاتی متغیر پاسخ را یاد بگیرد و بخش دیگر را نمیتواند بیاموزد. اگر اصرار کنیم که با پیچیدهتر کردن مدل، قسمت دیگر را نیز بیاموزد، مدل شروع به حفظ کردن آن میکند و علیرغم عملکرد عالی روی مجموعه دادهی آموزشی، عملکردش روی دادهی آزمون نامناسب خواهد بود. به این پدیده بیشبرازش[10] میگویند که برای هر مدل یادگیری ماشین ممکن است اتفاق بیفتد.
بنابراین باید تلاش کنیم تا مدل رگرسیونی، سطح بهینهای از واریانس متغیر پاسخ را یاد بگیرد و بقیهی آن را به جای صرفا حفظ کردن، رها کند. مجموع مربعات فاصلهی بین مقادیر پیشبینیشدهی مدل و میانگین متغیر پاسخ محاسبه شده و مجموع مربعات رگرسیونی نامیده میشوند. اگر این مقدار کوچک باشد، به این معنی است که مدل، پیشبینیهایی در حوالی میانگین متغیر پاسخ تولید میکند. در واقع در این حالت مدل به صورت کاملا محافظهکارانه تلاش میکند تا با نگه داشتن خود در نزدیکی میانگین متغیر هدف، همواره مقدار قابل توجیهی را پیشبینی کند. اگر مقدار مجموع مربعات رگرسیونی بزرگ باشد، یعنی مدل یاد گرفتهاست تا با فاصله گرفتن از مقدار میانگین متغیر پاسخ، جسورانهتر به پیشبینی بپردازد. در واقع مجموع مربعات رگرسیونی آن بخشی از تغییرات متغیر پاسخ است که مدل توانسته است آن را یاد بگیرد.
از طرفی، مجموع مربعات فاصله بین مقادیر پیشبینی شده توسط مدل و مقادیر واقعی متغیر پاسخ محاسبه میشود و "مجموع مربعات خطا" نام میگیرد. این مجموع مربعات خطا به وضوح نشاندهنده خطاهای کلی مدل است؛ به عبارت دیگر، آن بخشی از تغییرات متغیر پاسخ است که مدل نتوانسته است به درستی راه حلی ارائه دهد.
با کمی عملیات سادهی ریاضیاتی میتوان نشان داد که واریانس متغیر پاسخ دقیقا از جمع کردن مجموع مربعات رگرسیونی و مجموع مربعات خطا به دست میآید. در جدول 1 اجزاء تجزیهی واریانس و درجه آزادی آنها را ملاحظه میکنید.
جدول 1: اجزاء تجزیهی واریانس
نام | درجه آزادی | رابطه |
مجموع مربعات کل |
|
|
مجموع مربعات رگرسیونی |
|
|
مجموع مربعات خطا |
|
|
درجه آزادی: تعداد نمونههایی در بین ![]() که با دانستن مقدار مجموع مربعات مربوطه، مقدارشان آزادانه میتواند تغییر کند.
که با دانستن مقدار مجموع مربعات مربوطه، مقدارشان آزادانه میتواند تغییر کند.
![]() : میزان تغییرپذیری کل
: میزان تغییرپذیری کل ![]() ها حول
ها حول ![]() را نشان میدهد.
را نشان میدهد.
![]() : میزان تغییرپذیری بین
: میزان تغییرپذیری بین ![]() ها که توسط خط رگرسیونی برازش شده قابل توضیح است.
ها که توسط خط رگرسیونی برازش شده قابل توضیح است.
![]() : میزان تغییرپذیری بین
: میزان تغییرپذیری بین ![]() ها که توسط خط رگرسیونی برازش شده قابل توضیح نیست.
ها که توسط خط رگرسیونی برازش شده قابل توضیح نیست.
روابط جدول بالا با سادهسازی به فرم زیر قابل بازنویسی هستند:
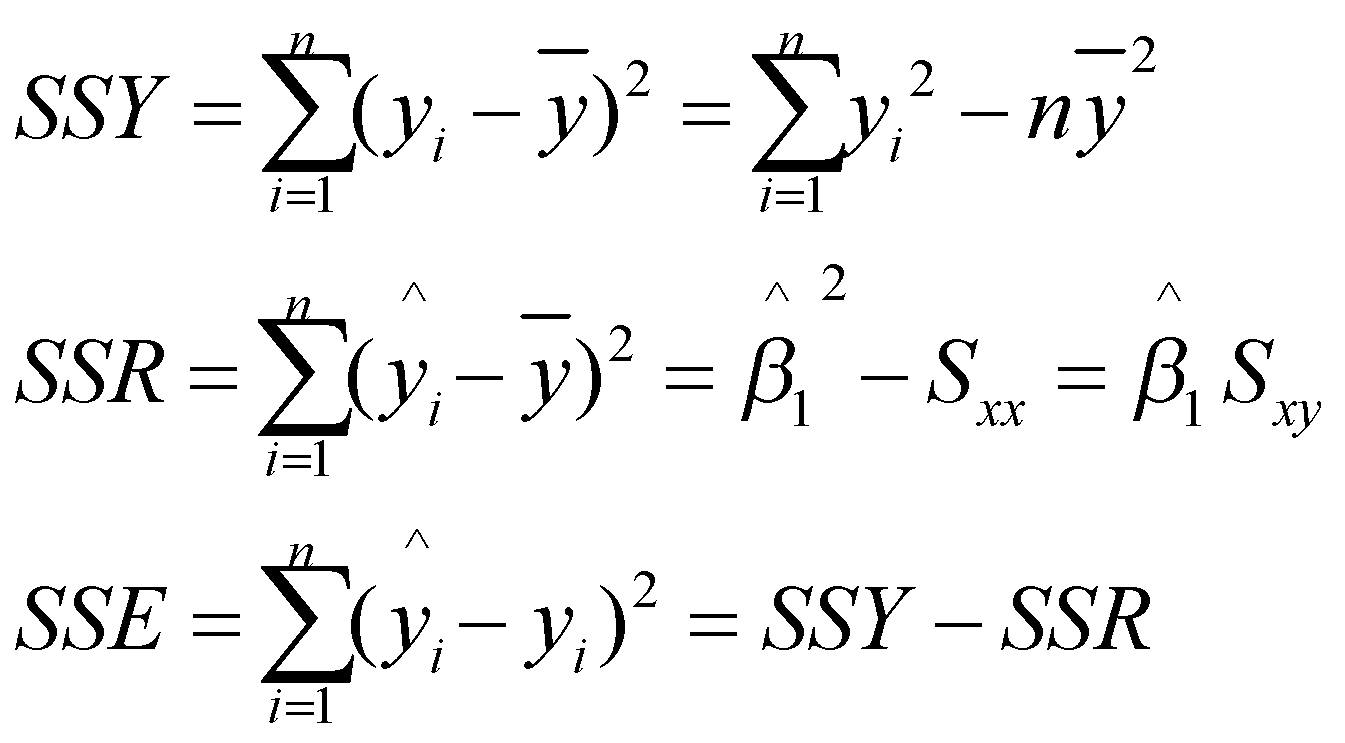
اگر هر کدام از مجموع مربعات به درجهی آزادیشان تقسیم شوند، میانگین مربعات مربوطه به دست میآید. آمارهی آزمون تجزیهی واریانس از تقسیم میانگین مربعات رگرسیونی بر میانگین مربعات خطا به دست میآید. ثابت میشود که این آماره از توزیع احتمال اف پیروی میکند. درجه آزادیهای توزیع (توزیع اف دارای دو درجهی آزادی است)، به ترتیب برابر درجهی آزادی مجموع مربعات رگرسیونی و مجموع مربعات خطا هستند یعنی:
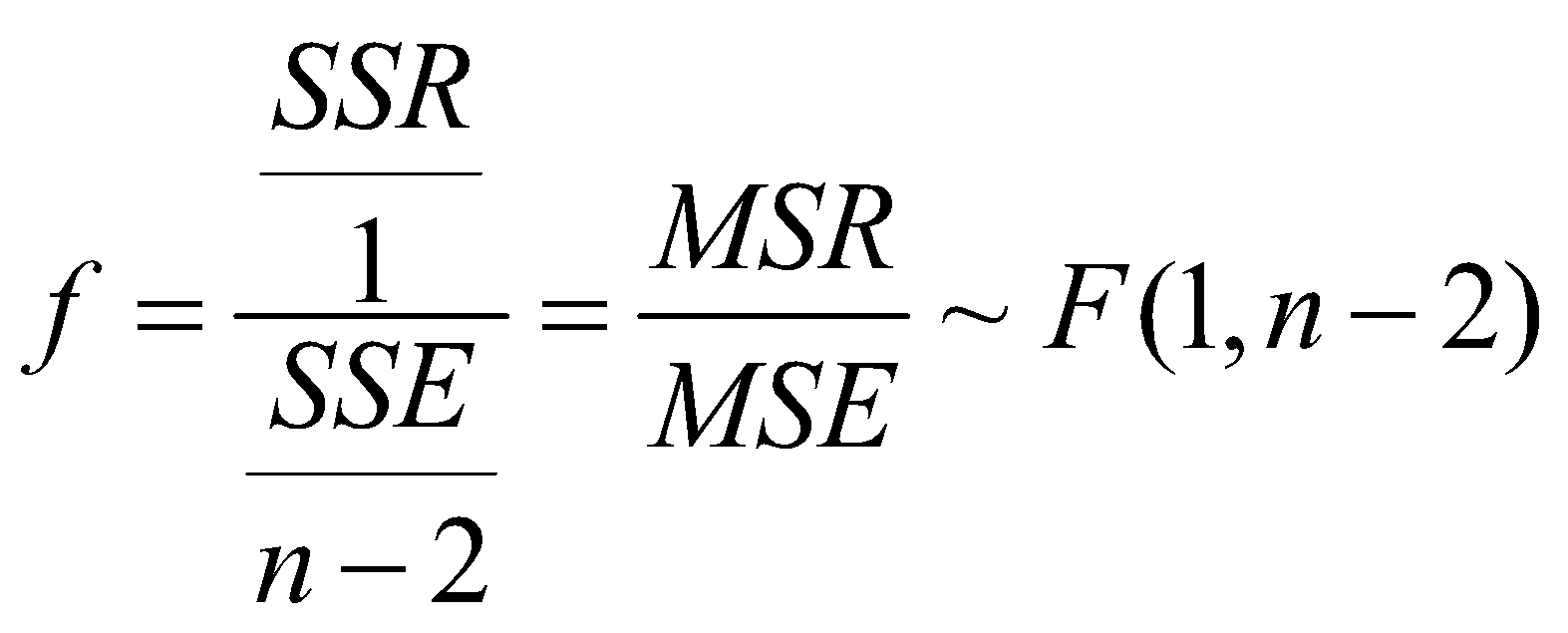
در آزمون تجزیهی واریانس به دنبال آزمون این فرض هستیم که آیا پارامتر شیب خط رگرسیونی برابر 0 است یا خیر. پس از محاسبهی آمارهی آزمون بالا، شرط زیر را چک میکنیم و در صورت برقرار بودن آن، فرض صفر رد میشود. فرض صفر در این آزمون 0 بودن شیب خط رگرسیونی است.
![]()
نکته: در آمار میدانیم که اگر داشته باشیم ![]() آنگاه
آنگاه ![]()
بنابراین داریم:
![]()
بنابراین آزمون تی و آزمون اف هر دو معادل هستند.
البته روش آزمون تی منعطفتر است و میتوان به کمک آن فرضهای ![]() ،
، ![]() ، و
، و ![]() را نیز آزمون کرد.
را نیز آزمون کرد.
تفسیر نتیجهی آزمون
اگر فرض صفر رد نشود یعنی هیچ رابطه خطی بین ![]() و
و ![]() وجود ندارد(یا اصلا رابطهای وجود ندارد یا رابطهی غیر خطی وجود دارد).
وجود ندارد(یا اصلا رابطهای وجود ندارد یا رابطهی غیر خطی وجود دارد).
اگر فرض صفر رد شود یعنی رابطه خطی بین ![]() و
و ![]() وجود دارد. رابطه خطی ممکن است قوی یا ضعیف باشد اما اندازهی شیب خط رگرسیونی قوی یا ضعیف بودن رابطه را نشان نمیدهد بلکه شدت رد فرض صفر میزان قوی بودن رابطه را نشان میدهد.
وجود دارد. رابطه خطی ممکن است قوی یا ضعیف باشد اما اندازهی شیب خط رگرسیونی قوی یا ضعیف بودن رابطه را نشان نمیدهد بلکه شدت رد فرض صفر میزان قوی بودن رابطه را نشان میدهد.
جدول تجزیهی واریانس
جدول 2: جدول تجزیهی واریانس
آماره آزمون | میانگین مربعات | درجه آزادی | مجموع مربعات | منبع تغییرات |
|
|
|
| رگرسیونی |
|
|
| باقیمانده(خطا) | |
|
| کل |
درجدولهای حاصل از خروجی نرمافزارهای کامپیوتری مقدار ![]() نمایش داده میشود.
نمایش داده میشود. ![]() یک مفهوم آماری است که تعریف دقیق ریاضیاتی دارد و در بسیاری از شاخههای دیگر علم نیز مورد استفاده است.
یک مفهوم آماری است که تعریف دقیق ریاضیاتی دارد و در بسیاری از شاخههای دیگر علم نیز مورد استفاده است. ![]() در واقع یک احتمال است؛ احتمال اینکه نمونههایی را مشاهده کنیم که از نمونهای که مشاهده کردهایم، قویتر فرض صفر را رد کنند.
در واقع یک احتمال است؛ احتمال اینکه نمونههایی را مشاهده کنیم که از نمونهای که مشاهده کردهایم، قویتر فرض صفر را رد کنند.
میتوان به بیان غیررسمی ![]() را میزان حمایت نمونهی مشاهدهشده از فرض صفر تلقی کرد و اگر مقدار آن کمتر از احتمال خطای نوع اول (
را میزان حمایت نمونهی مشاهدهشده از فرض صفر تلقی کرد و اگر مقدار آن کمتر از احتمال خطای نوع اول (![]() ) مورد نظر باشد، فرض صفر رد میشود و فرض مقابل در سطح اطمینان
) مورد نظر باشد، فرض صفر رد میشود و فرض مقابل در سطح اطمینان ![]() پذیرفته میشود.
پذیرفته میشود.
قبل از انجام هر آزمون آماری ابتدا باید احتمال خطای نوع اول مورد نظر را مشخص کنید. معمولا مقدار احتمال خطای نوع اول را برابر 0.05 در نظر میگیرند. با توجه به توضیحات بالا اگر ![]() در آزمونی که انجام گرفته کمتر از 0.05 بود، یعنی نمونهای که مشاهدهشده، با احتمال کمتر از 0.05 از فرض اولیه حمایت میکند؛ بنابراین فرض صفر را به نفع فرض مقابل رد میشود.
در آزمونی که انجام گرفته کمتر از 0.05 بود، یعنی نمونهای که مشاهدهشده، با احتمال کمتر از 0.05 از فرض اولیه حمایت میکند؛ بنابراین فرض صفر را به نفع فرض مقابل رد میشود.
اگر فرض نرمال بودن خطای اندازهگیری خط رگرسیونی را در نظر بگیریم، به کمک همین فرض میتوان بازهی اطمینان برای پارامترها ساخته شود.
فواصل اطمینان برای پارامترهای رگرسیونی
تا به ایجا یاد گرفتیم به کمک دو آزمون معرفیشده، مقدار پارامترها را در سطح اطمینانی معین آزمون کنیم. حال فرض کنید بخواهیم بازهای را برای یک پارامتر پیشنهاد بدهیم و ادعا کنیم که مقدار واقعی پارامتر مورد نظر مثلا با احتمال 95% درصد در این بازه قرار میگیرد. به کمک فرض نرمال بودن خطاها، میتوانیم این فواصل اطمینان را بسازیم و از آنها در تحلیلهایمان بهره ببریم.
روش ساخت بازه اطمینان در واقع مشابه یک روش استفاده شده در آزمون فرضیهها است. در آزمون فرضیهها، یک آماره به عنوان شاخص آزمون معرفی میشود و با مقایسه مقدار آن با چندکهای مختلف توزیع احتمال آماره، تصمیم درباره نتیجه آزمون گرفته میشود. اما وقتی هدف ساخت بازههای اطمینان است، باید یک کمیت محوری در آمارهسازی محاسبه شود.
علاوه بر این، برای ساخت بازه اطمینان، باید توزیع احتمال کمیت محوری مشخص شود و با استفاده از مقدار محاسبه شده از کمیت محوری و چندکهای توزیع احتمال، بازه مورد نظر محاسبه گردد.
ثابت میشود که تخمین پارامتر شیب خط رگرسیونی دارای توزیع نرمال به فرم زیر است:
بنا بر توزیع بالا، کمیت محوری به صورت زیر تعریف میشود که از توزیع احتمال تی پیروی میکند:
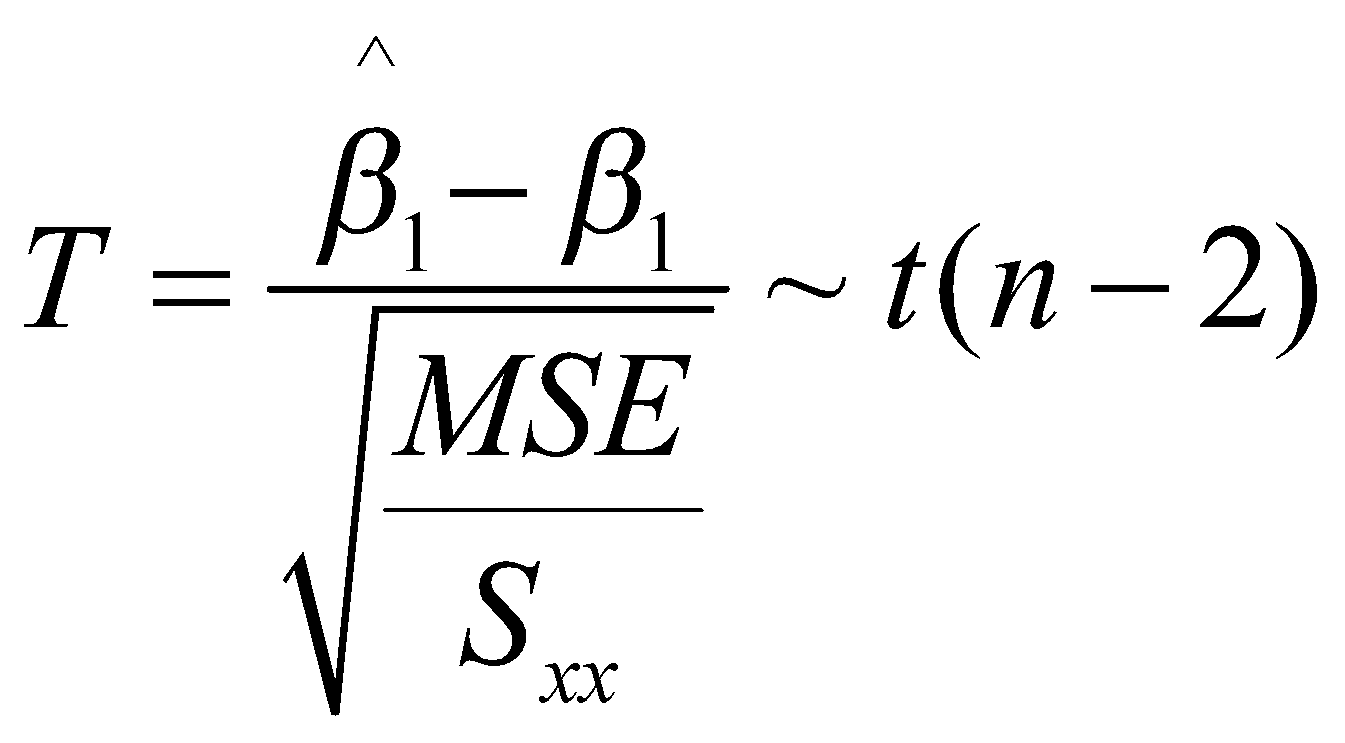
به طور رسمی کمیت محوری شاخصی است که تنها پارامتر مجهول آن، پارامتری است که میخواهیم برای آن بازهی اطمینان بیابیم و توزیع آن نیز به پارامتر مجهول دیگری وابسته نیست.
با دانستن مقدار و توزیع کمیت محوری میتوانیم بازهای با بیابیم که با احتمال دلخواه ما پارامتر مورد نظر را دربربگیرد:
![]()
به طور مشابه برای پارامتر عرض از مبدا خط رگرسیونی داریم:
![]()
کمیت محوری برای این پارامتر به صورت زیر تعریف میشود:
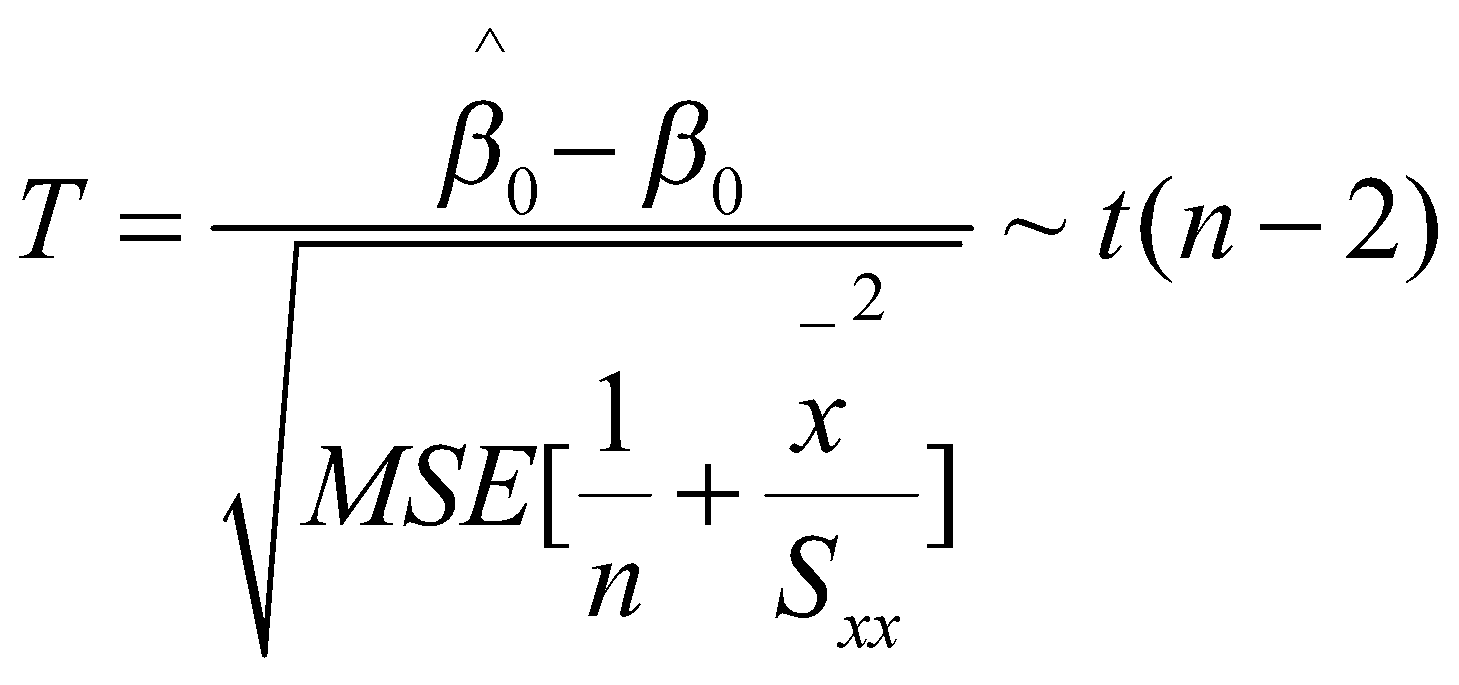
با کمی محاسبات آماری به بازهی اطمینان زیر میرسیم:
![]()
در ادامه سه بازهی اطمینان مفید دیگر را نیز ذکر میکنیم اما وارد جزییات مربوط به آنها نمیشویم.
برای پارامتر واریانس خطای رگرسیونی:
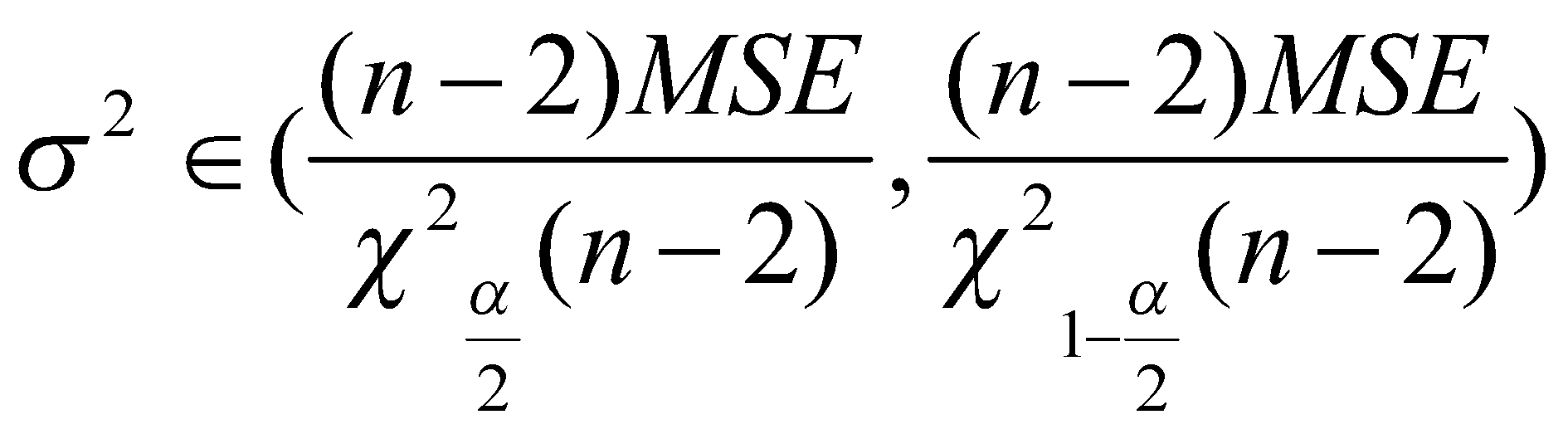
برای میانگین شرطی متغیر هدف:
![]()
برای متغیر وابسته متناسب با مشاهده جدید (فاصلهی پیشبینی):
![]()
جا دارد تا در اینجا به یک نکتهی مهم اشاره شود. فرضیات مدل رگرسیونی "فرض" هستند. یعنی ما در مرحلهی مدلسازی با این فرض جلو میرویم که مثلا میانگین خطای مدل 0 است و واریانس آن ثابت است. این فرضیات را باید بعد از مرحلهی مدلسازی با دقت بررسی کنیم زیرا مدل تنها در صورتی قابل اتکا است که فرضیاتی که براساس آنها مدل فرمولبندی شدهاست، برقرار باشند.
ضریب همبستگی
در فایل نظریه احتمال تا حدی دربارهی مفهوم هبستگی صحبت کردیم. متناسب با نوع و رفتار متغیرها ضرایب همبستگی متفاوتی معرفیشدهاند.
در مبحث رگرسیون، متغیر پاسخ از جنس عددی است. متغیر پیشگو میتواند کمّی یا کیفی باشد اما معمولا متغیر پیشگو نیز عددی است.
در آمار همبستگی به صورت زیر تعریف میشود:
![]()
ضریب هبستگی نمونهای پیرسون میزان ارتباط خطی دو متغیر پیوسته را اندازهگیری میکند. همواره بین 1- و 1+ مقدار میگیرد و به صورت زیر تعریف میشود:
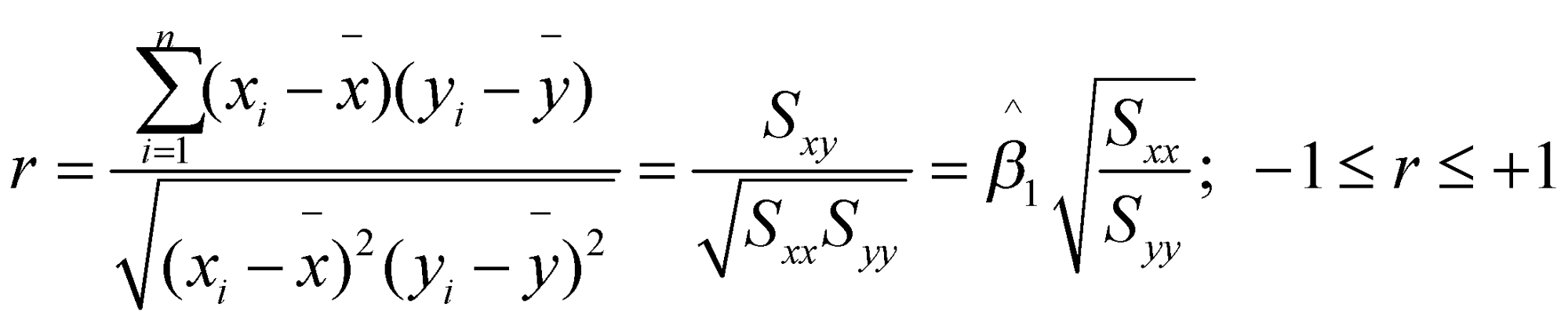
ما در رگرسیون خطی به دنبال پیدا کردن رابطهی خطی هستیم بنابراین ضریب همبستگی پیرسونی میتواند در تشخیص جهت و شدت این رابطهی خطی کمک کند.
در شکل 4، سه حالت کلی همبستگی خطی دو متغیر نمایش داده شده است. در شکل سمت چپ، یک ارتباط خطی با جهت (شیب) مثبت بین دو متغیر موجود است. به این معنا که با افزایش یک متغیر، دومی نیز افزایش مییابد و با کاهش هرکدام، دیگری نیز کاهش خواهد یافت. در شکل وسط، یک رابطهی خطی با جهت ( شیب) منفی بین دو متغیر وجود دارد. یعنی با رفتار دو متغیر بر خلاف جهت یکدیگر در قالب یک رابطهی خطی تغییر میکند. در شکل سمت راست، هیچ ارتباط خطیای مشاهده نمیشود. میبینیم که به ازای تمام مقادیر متغیر محور افقی، مقدار مغیر محور عمودی تغییری نمیکند.
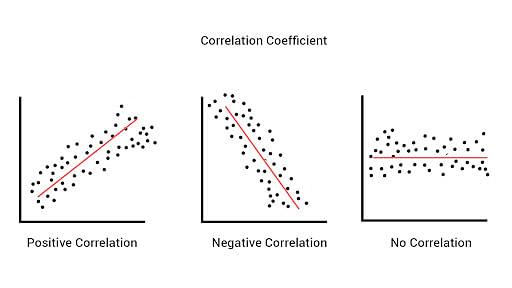
شکل 4: شهود هندسی انواع همبستگی خطی
ضریب تعیین
ضریب تعیین یک شاخص بسیار مهم است که نشان میدهد چقدر مدلی که به مجموعه دادههای آموزشی برازش دادهایم، مفید و کارا است. این ضریب در واقع نسبتی است که با استفاده از مجموع مربعات رگرسیونی (SSR) محاسبه میشود. SSR نشان میدهد که مدل چه قدر توانسته است تغییرات متغیر پاسخ را توضیح دهد. در سمت دیگر، مجموع مربعات خطا (SSE) نشاندهنده پراکندگی واریانس متغیر پاسخ است که مدل نتوانسته است آن را یاد بگیرد. با محاسبه ضریب تعیین، ما میتوانیم ببینیم که مدل به چه اندازه توانسته است دادههای آموزشی را تبیین کند.
پس طبیعی است که اگر مجموع مربعات رگرسیونی را به مجموع مربعات خطا تقسیم کنیم و دوست داشت باشیم که مقدار آن بزرگ باشد. از طرفی میدانیم مجموع صورت و مخرج این کسر ثابت و برابر واریانس متغیر پاسخ است، مقدار این کسر همواره بین صفر و یک خواهد بود.
![]()
پس ضریب تعیین در واقع نسبت مزیتهای مدل به کاستیهای مدل است و هرچه مقدار آن بیشتر باشد (به شرط برقراری فرضهای مدل رگرسیونی) به معنای عملکرد مناسب مدل است.
مقدار مناسبی را نمیتوان برای ضریب تعیین مشخص کرد و از مسالهای به مسالهی دیگر متفاوت است اما به طور کلی مقادیر بالای ۰.۷ قابلقبول هستند.
تا اینجای راجعبه مقدمات رگرسیون صحبت کردیم باقی مطالب را در قسمت دوم خواهیم دید.
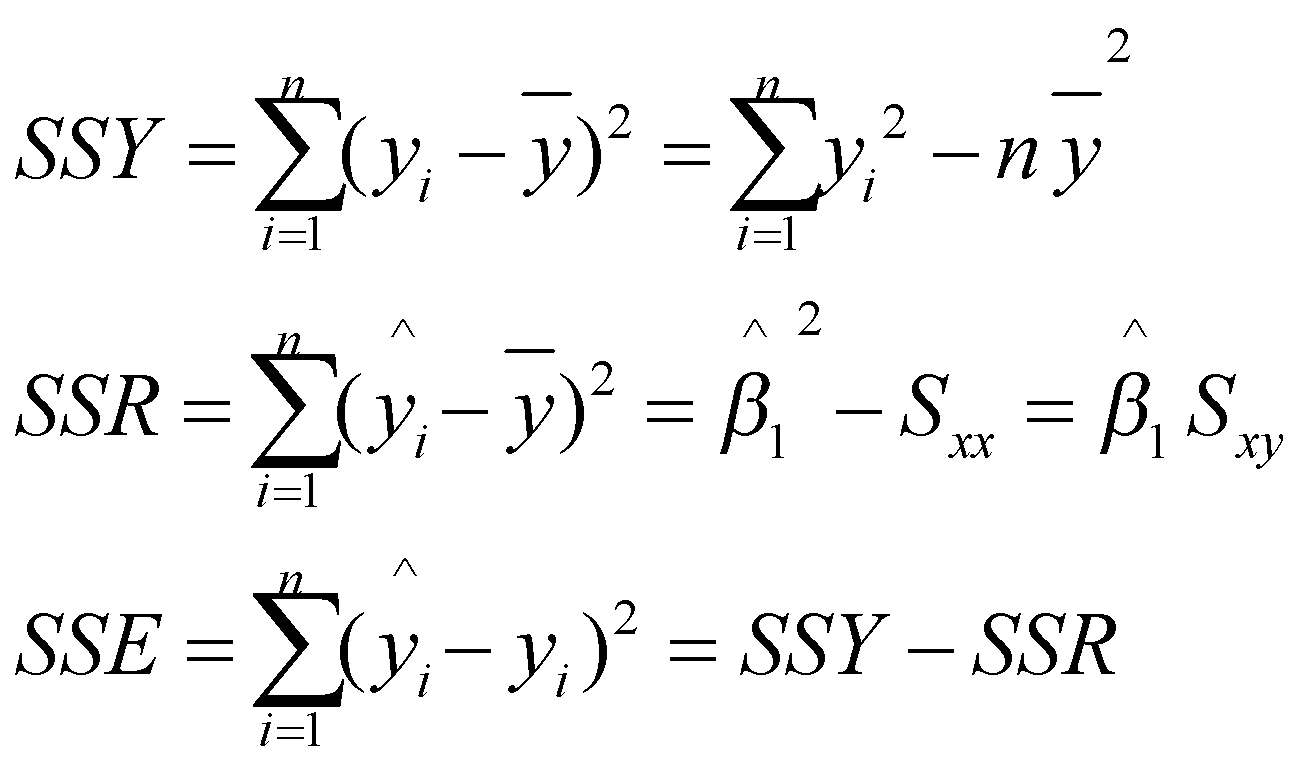
نظرات