خلاصه‌ای بر نظریه احتمال قسمت دوم
مقدمه
در قسمت قبل با مفهوم نظریه احتمال و مبانی مهمی مثل واریانس، امید ریاضی، توزیع احتمال و انواعشان آشنا شدیم. در این قسمت ابتدا تعداد دیگری توزیع معرفی و بقیه مباحث آشنایی آمار در هوش مصنوعی مانند تحلیل رگرسیون، قضیه بیز و مطالب دیگری به همراه تعدادی مثال توضیح می‌دهیم.
- توزیع پواسون
یک متغیر تصادفی که تعداد رخداد یک اتفاق خاص را که به طور متوسط با نرخ 
در یک بازه‌ی زمانی یا مکانی مشخص اتفاق می‌افتد را نشان می‌دهد، دارای توزیع پواسون است. از این توزیع می‌توان برای مدلسازی اتفاقاتی نظیر زیر استفاده کرد:
- تعداد بارش‌های شهابی در سال
- تعداد گل‌ها در یک مسابقه‌ی فوتبال
- تعداد بیمارانی که بین ساعت 10 الی 11 شب به اورژانس مراجعه می‌کنند.
- تعداد فوتون‌های لیزر که در یک بازه‌ی زمانی مشخص به یک سطح خاص برخورد می‌کنند.
- تعداد مشتریانی که در طی روز به فروشگاه یا وب‌سایت مراجعه می‌کنند.
متغیر تصادفی پواسون، ذاتا گسسته است. هم میانگین و هم واریانس توزیع پواسون، برابر است. مقدار پارامتر می تواند در بازه صفر تا 
باشد.
تابع جرم احتمال توزیع پواسون به صورت زیر است:
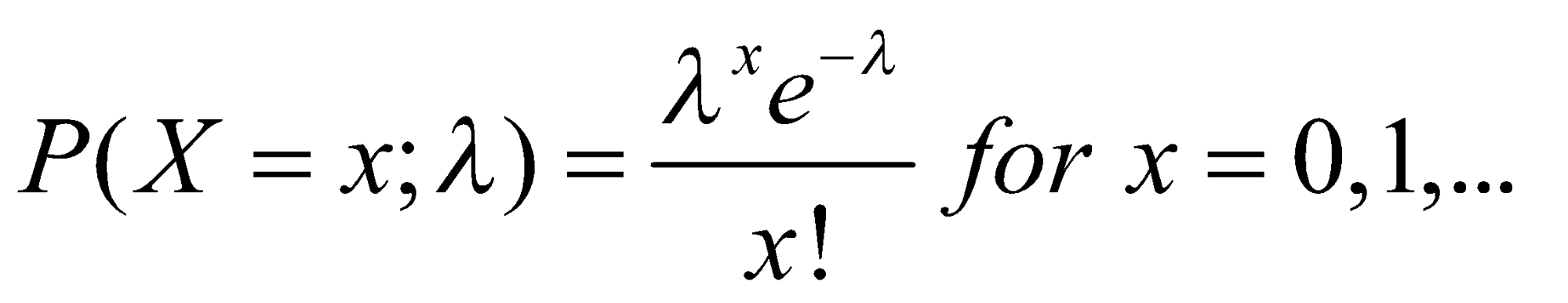
در شکل 18 و 19 رفتار تابع جرم احتمال و توزیع تجمعی احتمال توزیع پواسون را به ازای مقادیر مختلف مشاهده می‌کنید.
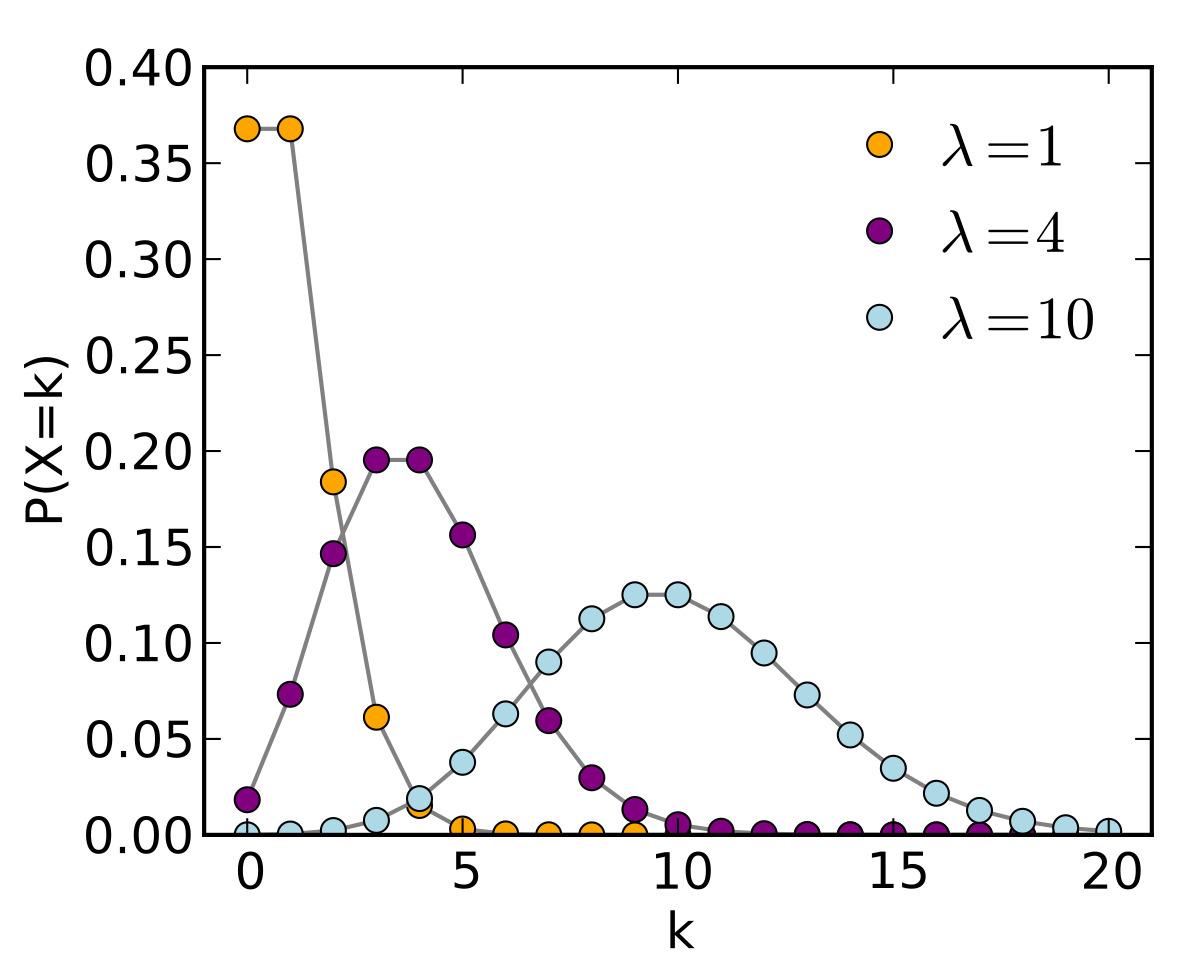
شکل 18: نمودار تابع جرم توزیع پواسون به ازای مقادیر مختلف
تابع توزیع تجمعی توزیع پواسون به فرم زیر است:
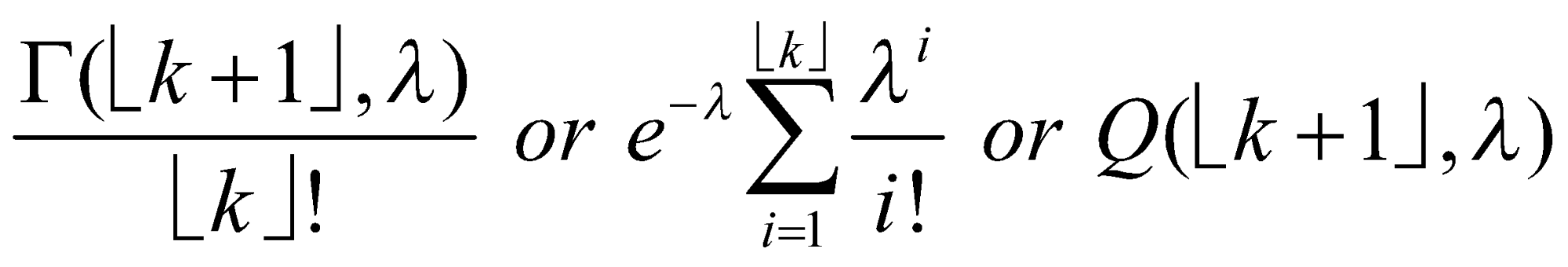
به ازای 
، 
برابر کران بالای تابع گامای ناکامل است. منظور از 
، تابع کف (رند رو به پایین) است و 
تابع گامای اصلاح‌شده است.
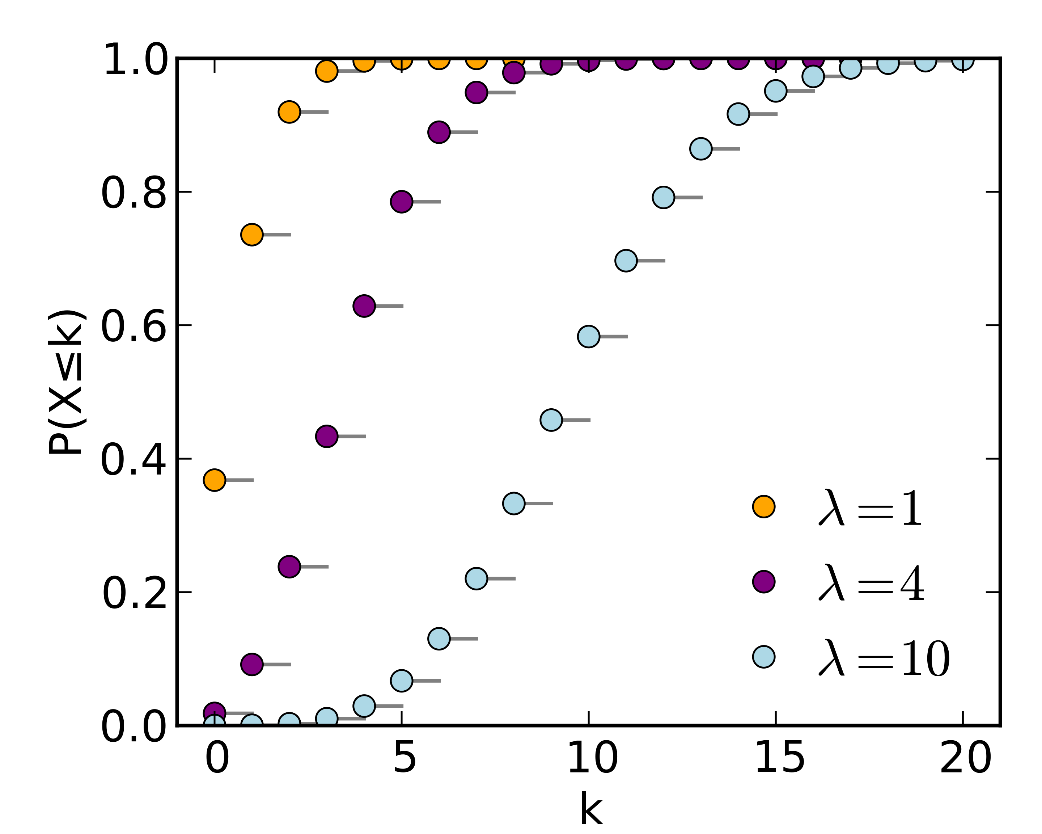
شکل 19: نمودار تابع توزیع احتمال توزیع پواسون به ازای مقادیر مختلف 
موارد استفاده‌ی توزیع پواسون
مدلسازی داده‌های شمارشی به صورت نرخ رخداد در بازه زمانی معین، مانند داده‌های بقا، تشعشعات رادیواکتیو، جداول توافقی فراوانی و سایر موارد با توزیع پواسون نشان داده می‌شوند.
تقریب توزیع دوجمله‌ای وقتی که 
بزرگ و 
کوچک است.
شهود ریاضیاتی توزیع پواسون
برای شهود ریاضی توزیع پواسون 
را یک بازه‌ی زمانی بسیار کوچک در نظر بگیرید. حال اگر فرض کنیم که احتمال رخداد یک اتفاق در بازه‌ی زمانی برابر با 
باشد، و احتمال وقوع بیش از یک رخداد، قابل چشم‌پوشی باشد و همچنین فرض کنیم که وقوع یا عدم وقوع اتفاق در یک بازه، مستقل از وقوع یا عدم وقوع اتفاق در یک بازه‌ی دیگر باشد، آنگاه تعداد رخدادهایی که در یک بازه‌ی زمانی اتفاق می‌افتد، دارای توزیع پواسون با نرخ است.
توزیع پواسون و نرخ وقوع
از توزیع پواسون برای مدل‌بندی نرخ رخداد اتفاقات استفاده می‌شود. اگر 
، آنگاه 
برابر تعداد وقوع مورد انتظار در یک بازه‌ی زمانی است. منظور از 
، کل زمان آزمایش است.
تقریب توزیع دوجمله‌ای با توزیع پواسون
یک متغیر تصادفی دوجمله‌ای از مجموع متغیر تصادفی مستقل برنولی با احتمال موفقیت است. از این توزیع برای مدل‌بندی تعداد موفقیت‌ها در تعداد مشخصی از آزمایش‌های باینری همسان، مانند تعداد دفعات مشاهده‌ی شیر در پنج بار پرتاب سکه استفاده می‌شود. وقتی که بزرگ و کوچک است (
)، توزیع پواسون یک تقریب دقیق برای توزیع دوجمله‌ای خواهد بود. در توزیع تقریب‌زننده داریم: 
در ادامه چند مثال توضیح می‌دهیم.
مثال یک)
فرض کنید متوسط تعداد مسافرانی که در یک ساعت سوار اتوبوس می‌شوند، برابر با 2.5 است. اگر اتوبوس را برای 4 ساعت مدنظر داشته باشیم، احتمال اینکه در این بازه‌ی زمانی تعداد 3 نفر یا کمتر مسافر مشاهده کنیم چقدر است؟ پاسخ در کد زیر قابل‌مشاهده است. ماژول stats کتابخانه‌ی scipy امکانات مناسبی را برای محاسبات آماری در اختیارمان قرار می‌دهد. توزیع پواسون به صورت یک کلاس در این ماژول پیاده‌سازی شده است و از طریق متد cdf می‌توانیم به تابع توزیع پواسون دسترسی داشته باشیم.
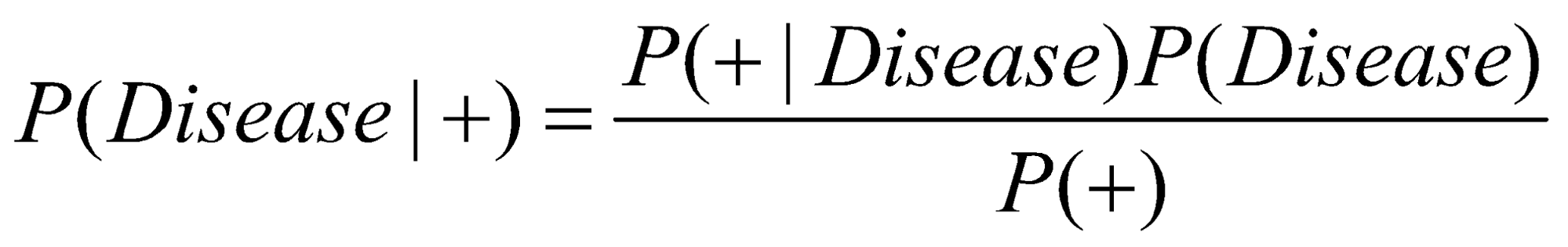
مثال دو)
اگر یک سکه با احتمال شیر آمدن 0.01 را 500 بار پرتاب کنیم، احتمال دو بار مشاهده‌ی شیر یا کمتر چقدر است؟
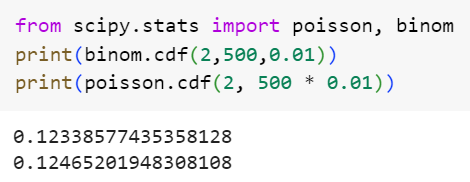
همانطور که مشاهده می‌کنید، تقریب توزیع پواسون برای توزیع دوجمله‌ای با دقت بسیار خوبی عمل می‌کند.
- توزیع یکنواخت
توزیع یکنواخت (یا توزیع مستطیلی) یک توزیع پیوسته است به طوری که همه‌ی فواصل با طول مساوی روی تکیه‌گاه (ساپورت) توزیع، دارای احتمال برابر هستند. برای مثال، این توزیع ممکن است برای مدل‌بندی تاریخ تولد افراد استفاده شود، زیرا فرض می‌شود همه روزهای سال تقویمی برای متولدین، به یک اندازه محتمل هستند. توزیع یکنواخت آزمایشی را توصیف می‌کند که در آن یک نتیجه‌ی تصادفی وجود دارد که بین مرزهای خاصی محدود شده است. کران‌های توزیع با پارامترهای 
و
که مقادیر حداقل و حداکثر متغیر تصادفی هستند، تعریف می‌شوند. بازه می‌تواند بسته یا باز باشد (
یا 
( بنابراین، توزیع یکنواخت به اختصار با 
نمایش داده می‌شود.
تابع چگالی جرم احتمال توزیع یکنواخت به صورت زیر مشخص می‌شود:
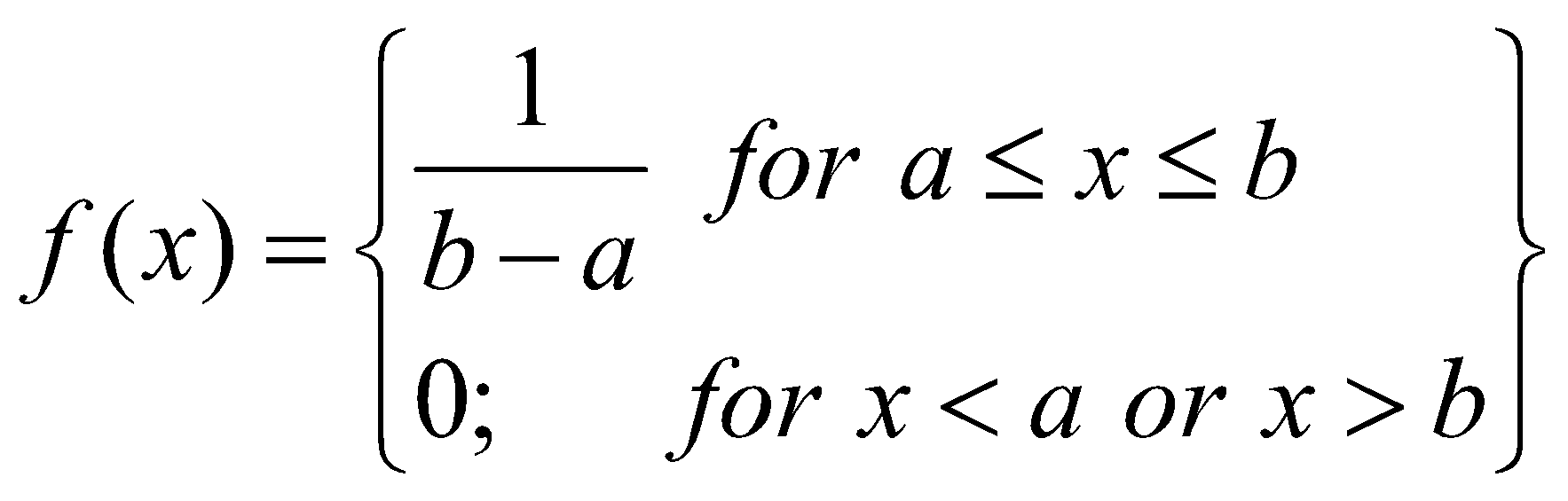
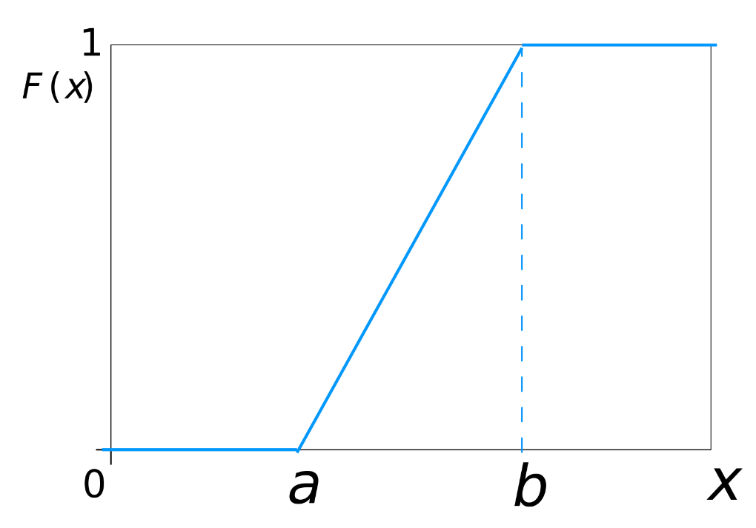
در شکل 20 و 21 تابع چگالی و توزیع تجمعی توزیع یکنواخت را مشاهده می‌کنید.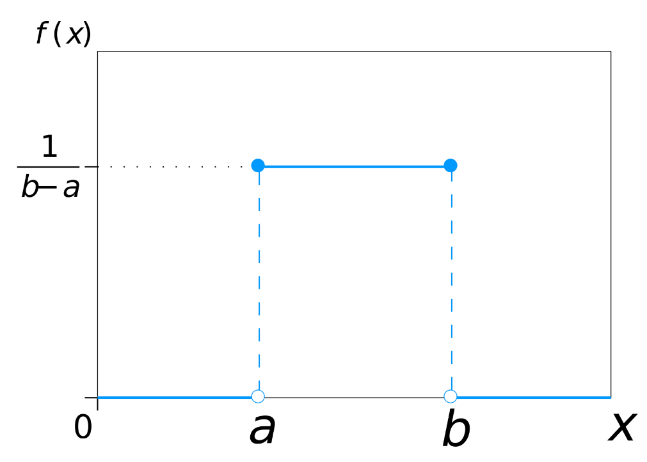
شکل 20: نمودار تابع چگالی احتمال توزیع یکنواخت
تابع توزیع تجمعی توزیع یکنواخت به صورت زیر قابل فرمول‌بندی است:
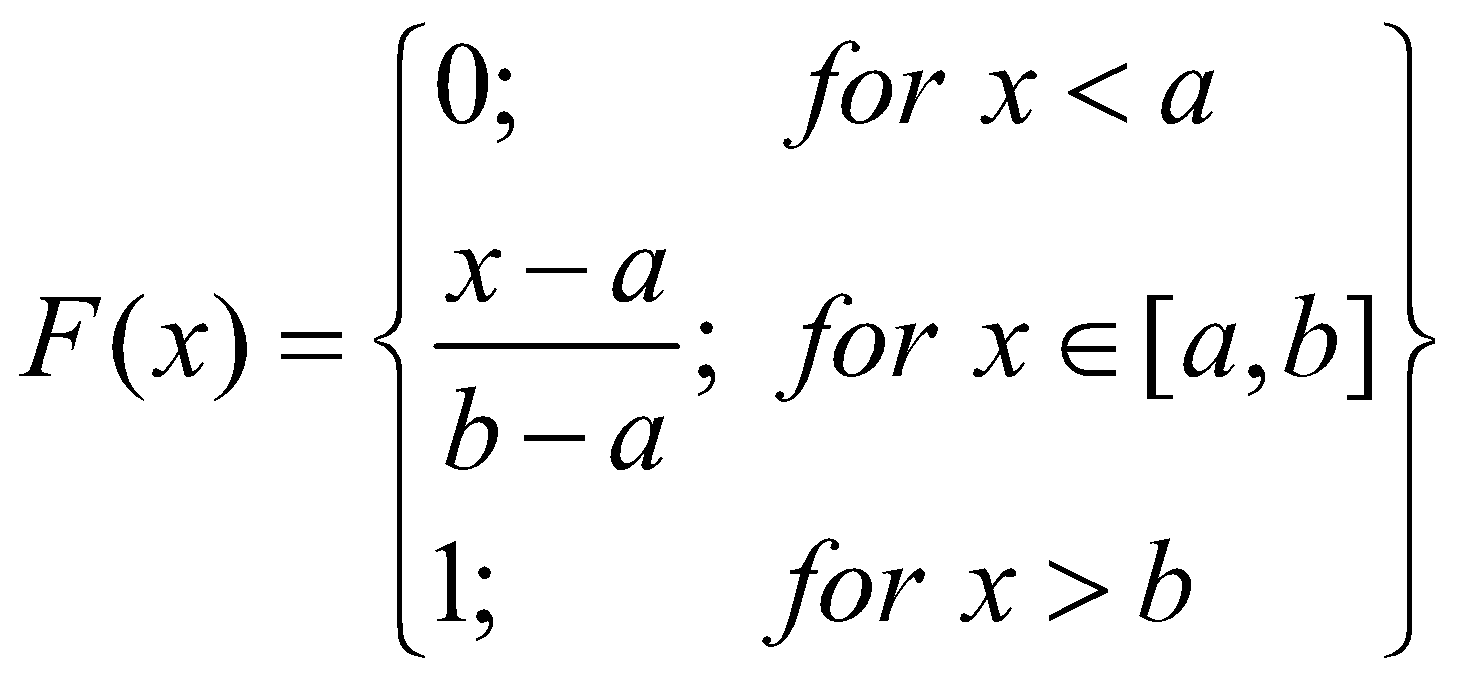
شکل 21: نمودار تابع توزیع تجمعی توزیع یکنواخت
- توزیع هندسی
یک متغیر تصادفی هندسی، تعداد آزمایش‌هایی را که برای مشاهده‌ی یک موفقیت مورد نیاز است، شمارش می‌کند که در آن هر آزمایش مستقل است و احتمال موفقیت دارد. بنابراین یک متغیر تصادفی هندسی، یک توزیع گسسته را مدل می‌کند. به عنوان مثال، از این توزیع می توان برای مدل‌بندی تعداد دفعاتی که یک تاس باید پرتاب شود تا عدد شش مشاهده شود، استفاده کرد.
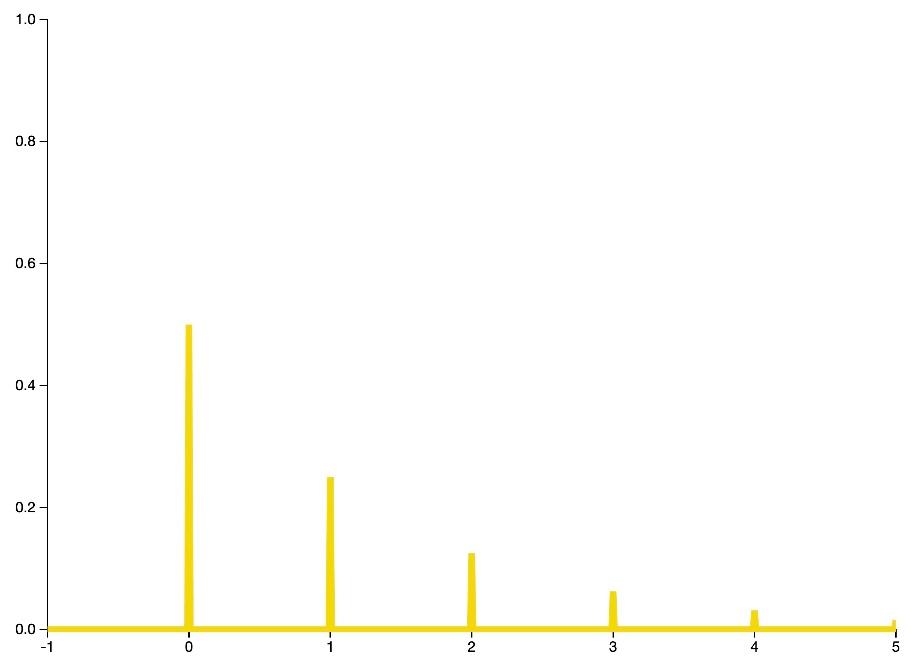
شکل 22: فرم کلی تابع جرم احتمال توزیع هندسی
- توزیع تی استیودنت
توزیع تی استیودنت (یا به اختصار، توزیع تی)، یک توزیع احتمال پیوسته است که برای تخمین میانگین یک جامعه‌ی نرمال در شرایطی که حجم نمونه کوچک است و انحراف استاندارد (انحراف معیار میانگین) جمعیت ناشناخته است، استفاده می‌شود.
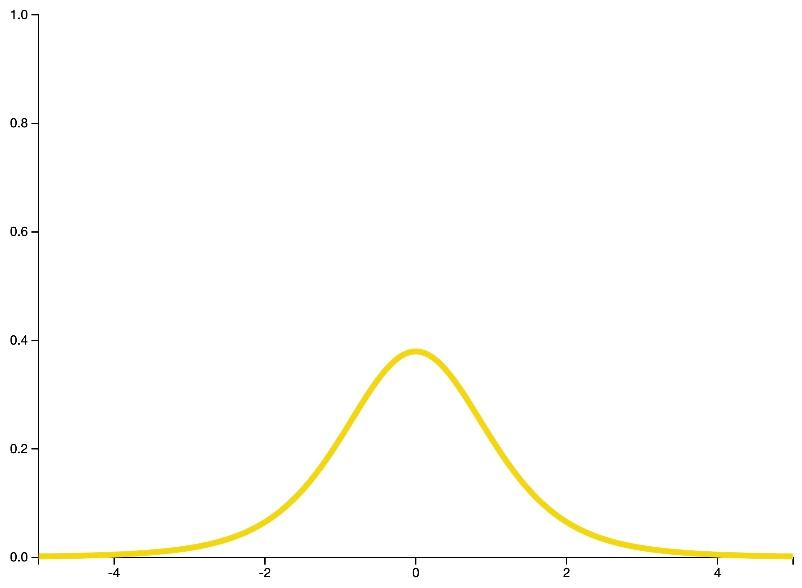
شکل 23: فرم کلی تابع چگالی احتمال توزیع تی
یک متغیر تصادفی کای دو با 
درجه آزادی، مجموع مجذور متغیر تصادفی نرمال استاندارد مستقل و هم‌توزیع است. بنابراین یک متغیر تصادفی کای دو، یک توزیع پیوسته را مدل می‌کند. از این توزیع اغلب در آزمون فرض‌ها و در ساخت فواصل اطمینان استفاده می‌شود.
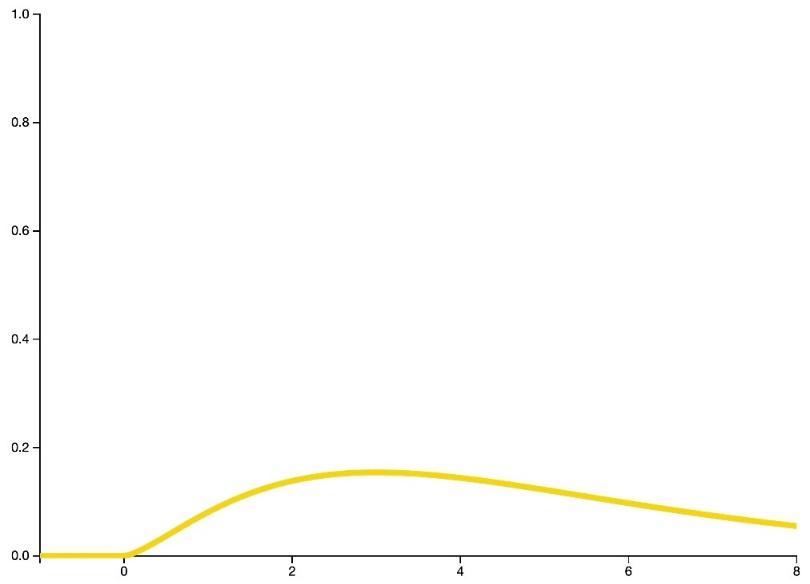
شکل 24: فرم کلی تابع چگالی احتمال توزیع کای دو
- توزیع نمایی
توزیع نمایی معادل پیوسته‌ی توزیع هندسی است. توزیع نمایی اغلب برای مدلسازی زمان انتظار استفاده می‌شود.
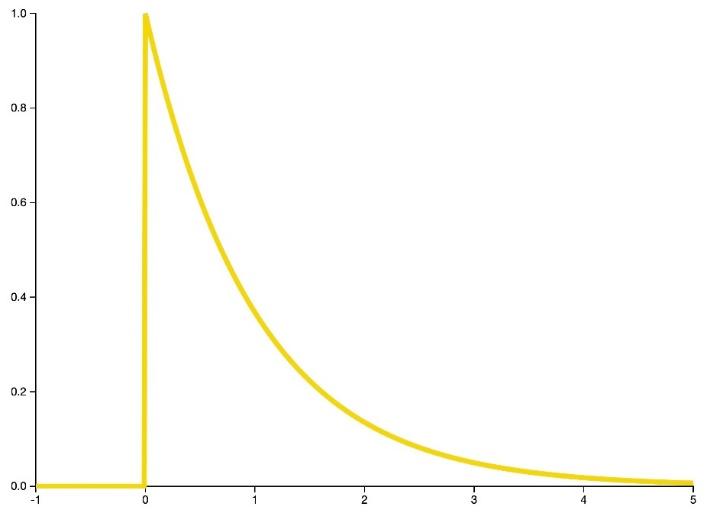
شکل 25: فرم کلی تابع چگالی احتمال توزیع نمایی
- توزیع اِف
توزیع اف که با عنوان توزیع فیشر - اسندکور نیز شناخته می‌شود، یک توزیع پیوسته است که اغلب به عنوان توزیع تحت فرض صفر (اولیه) آماره‌ی آزمون ، به ویژه در آزمون تجزیه‌ی واریانس، استفاده می‌شود.
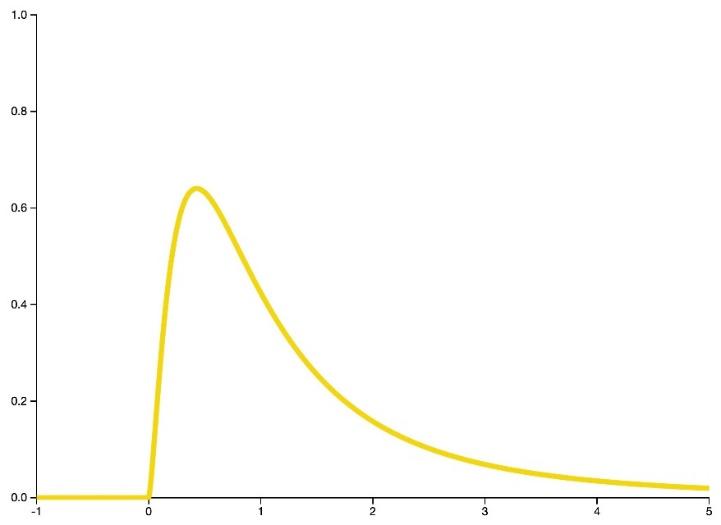
شکل 26: فرم کلی تابع چگالی احتمال توزیع اف
- توزیع گاما
توزیع گاما یک خانواده‌ی کلی از توزیع‌های احتمال پیوسته است. توزیع نمایی و کای دو، موارد خاصی از توزیع گاما هستند.
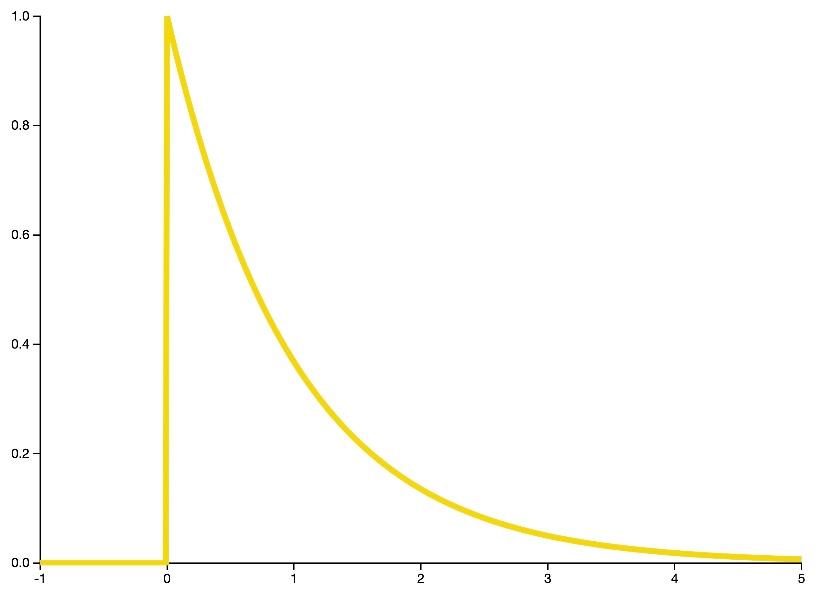
شکل 27: فرم کلی تابع چگالی احتمال توزیع گاما
- توزیع بتا
توزیع بتا یک خانواده‌ی کلی از توزیع‌های احتمال پیوسته است که بین 0 و 1 محدود شده است. توزیع بتا اغلب به عنوان توزیع مزدوج پیشین در آمار بیزی استفاده می‌شود.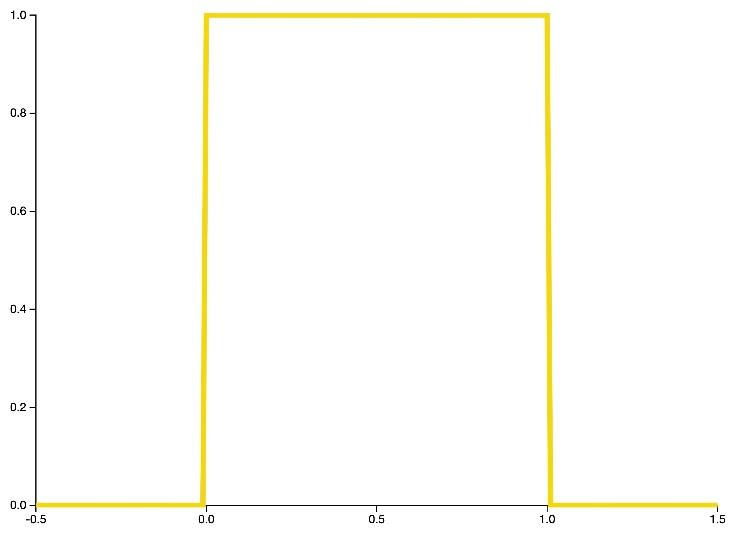
شکل 28: فرم کلی تابع چگالی احتمال توزیع بتا
- آمار فراوانی‌گرایانه
آمار فراوانی‌گرایانه رویکرد تعیین ویژگی‌های یک توزیع احتمال پنهان، از طریق مشاهده‌ی داده‌ها است. در این رویکرد اساس کار نمونهی مشاهده‌شده است و باورهای پیشین ما در مورد آزمایش تصادفی، هیچ جایگاهی در روند استنباط آماری ندارند.
- برآورد نقطه‌ای
یکی از اهداف اصلی علم آمار، تخمین پارامترهای ناشناخته است. برای تقریب این پارامترها، ما یک برآوردگر را انتخاب می‌کنیم که تابعی از مشاهدات نمونهی تصادفی است. برای نشان دادن نحوه‌ی کار این ایده، اجازه دهید مسئله‌ی تخمین مقدار عدد 
را در نظر بگیریم. برای انجام این کار، می‌توانیم نقاطی را به عنوان نمونهی تصادفی از مربعی که داخل آن یک دایره‌ای محاط شده است انتخاب کنیم. توجه داشته باشید که مقدار را می‌توان به عنوان نسبت مساحت‌ها بیان کرد. می‌دانیم که:
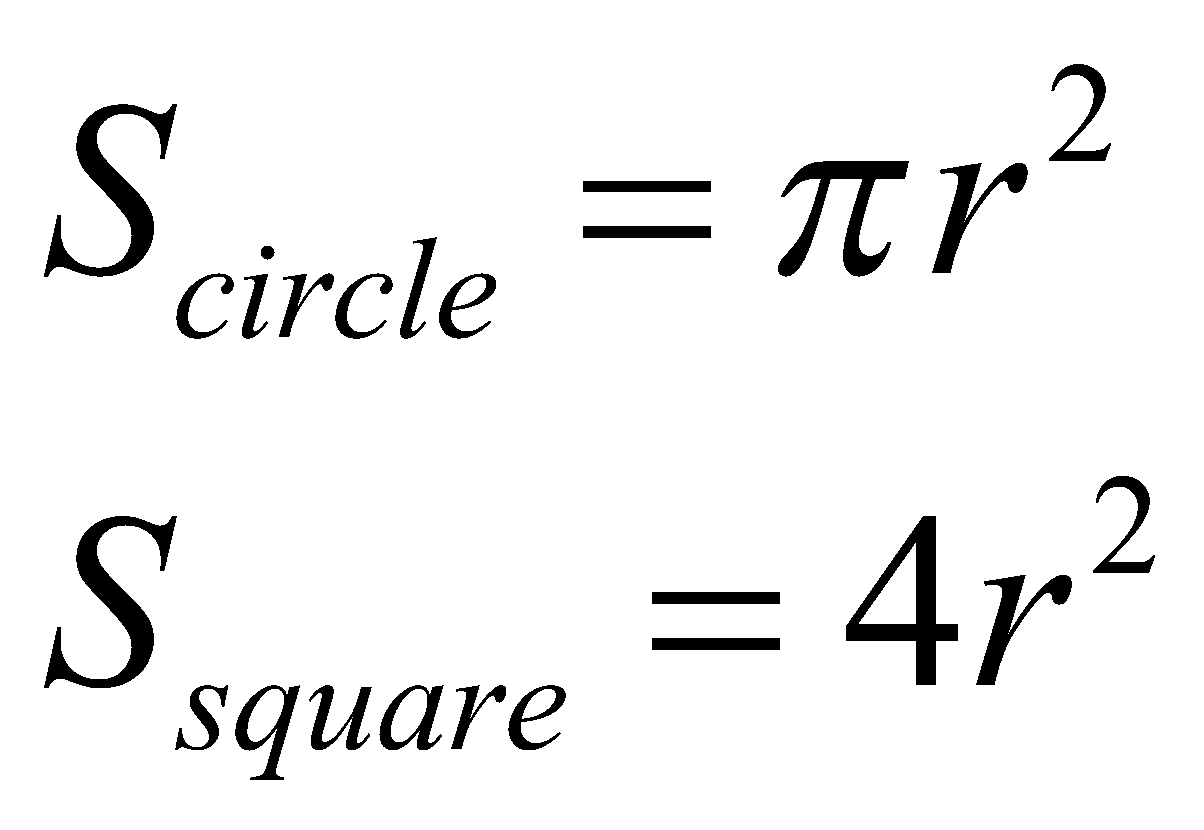
در نتیجه داریم:
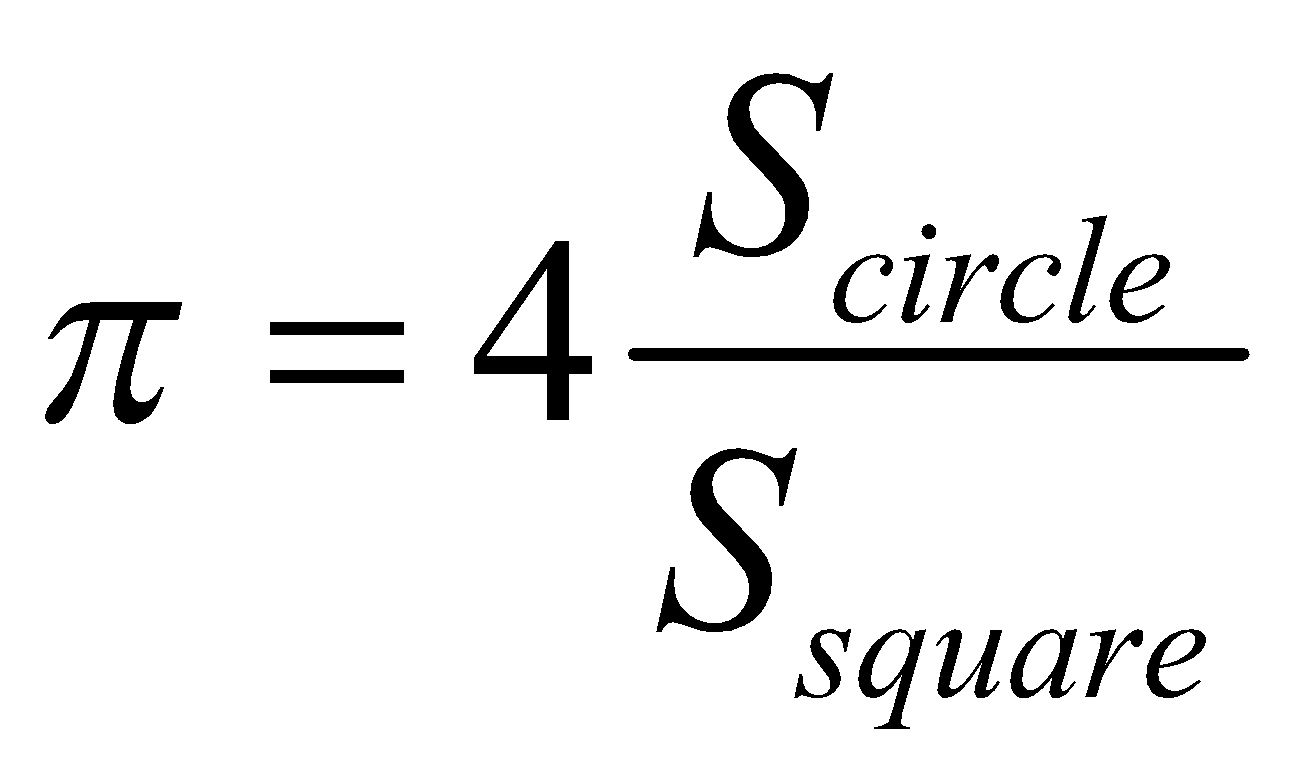
می‌توانیم نسبت بالا را به کمک نمونهی تصادفی‌مان تخمین بزنیم. فرض کنید 
تعداد نمونه‌های داخل دایره و تعداد کل نمونه‌های به دست آمده باشد. تخمین‌گر 
را به صورت زیر تعریف می‌کنیم:
می‌توان نشان داد که این برآوردگر دارای ویژگی‌های مطلوب بی‌طرفی و سازگاری است.
- بازه‌ی اطمینان
بر خلاف برآوردگرهای نقطه‌ای، فواصل اطمینان، پارامتر را با تعیین بازه‌ای از مقادیر ممکن برای پارامتر تخمین می‌زند. این بازه با یک سطح اطمینان همراه است. سطح اطمینان احتمال این را نشان می‌دهد که فرایند تولید بازه، پارامتر واقعی را دربربگیرد.
بسیاری از استنباط‌های متداول بر پایه استفاده از برآوردگرهای مناسب متمرکز هستند. با این حال، یافتن توزیع احتمال دقیق این برآوردگرها به صورت تحلیلی اغلب دشوار است. تکنیک محاسباتی معروف به بوت‌استرپ روشی مناسب برای تخمین پارامترها به کمک بازنمونه‌گیری به دفعات زیاد است.
- استنباط بیزی
تکنیک‌های استنباط بیزی کمک می‌کنند که با مشاهده داده‌های موجود، باورهای اولیه‌ی خود را در مورد مسئله به‌روزرسانی کنیم.
- قضیه‌ی بیز
فرض کنید در آخرین ملاقات خود در مطب پزشک، تصمیم به انجام آزمایشی برای یک بیماری نادر گرفته‌اید. اگر به اندازه کافی بدشانس باشید که نتیجه‌ی مثبت دریافت کنید، سوال منطقی بعدی این است که «با توجه به نتیجه آزمایش، احتمال اینکه من واقعاً به این بیماری مبتلا شده باشم چقدر است؟» (زیرا به هر حال، آزمایش‌های پزشکی کاملاً دقیق نیستند) قضیه بیز دقیقاً به ما می‌گوید که چگونه این احتمال را محاسبه کنیم:
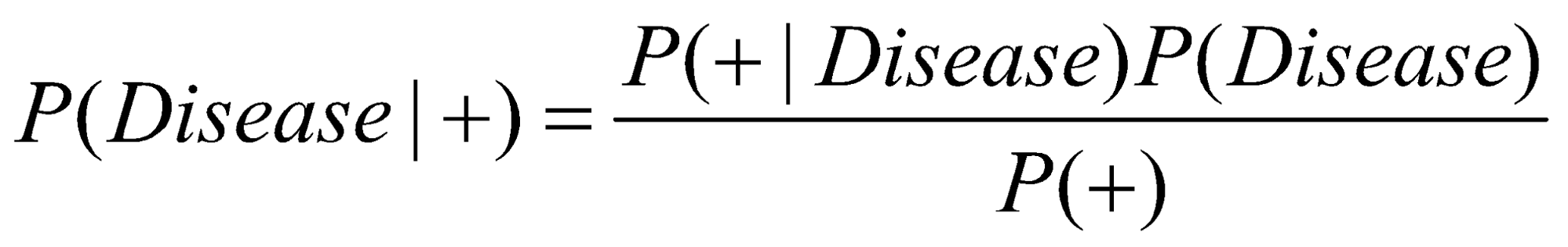
همانطور که معادله‌ی بالا نشان می‌دهد، احتمال ابتلا به بیماری با توجه به مثبت بودن آزمایش، بستگی به احتمال پیشین بیماری (
) دارد. این احتمال را به عنوان نرخ شیوع بیماری در جمعیت عمومی در نظر بگیرید.
احتمال پسین به دقت آزمایش (
) نیز بستگی دارد. یعنی در چند درصد مواقع، آزمایش به درستی نتیجه‌ی منفی را برای یک فرد سالم گزارش می‌کند و در چند درصد مواقع، نتیجه مثبت را برای فرد بیمار گزارش می‌کند؟
- تابع Likelihood
در آمار تابع likelihood تابع بسیار مفید و مهمی است:
تابع likelihoodدر هر دو بخش آمار فراوانی‌گرایانه و بیزی کاربردهای فراوانی دارد. به طور کلی این تابع، تابع احتمالی است که جای ورودی و شرط آن عوض‌شده‌است. یعنی نمونهی مشاهده‌شده را به عنوان شرط لحاظ می‌کند و مقادیر مختلف پارامترهای توزیع را به عنوان ورودی می‌گیرد. سپس به اینکه چقدر محتمل است نمونهی مشاهده‌شده، تحت پارامترهای ورودی، تولید شده باشد، یک مقدار احتمال نظیر می‌کند.
- از توزیع پیشین تا توزیع پسین
هسته اصلی آمار بیزی این ایده است که با به دست آوردن داده‌ها و نمونه‌های جدید، باورهای قبلی ما درباره‌ی موضوع باید به‌روزرسانی شوند. یک سکه‌ی ناسالم را در نظر بگیرید که با احتمال شیر می‌آید. همانطور که داده‌ها را با پرتاب سکه به دست می‌آوریم، توزیع پسین را که بهترین حدس ما را در مورد مقادیر احتمالی بایاس سکه نشان می‌دهد، به‌روزرسانی می‌کنیم. سپس این توزیع به‌روزرسانی شده را به عنوان توزیع پیشین برای پرتاب سکه‌ی بعدی در نظر می‌گیریم. به صورت کلی این فرایند را می‌توان به دو صورت انجام داد. یک رویکرد کاملاً تئوری است که در آن تلاش می‌شود با استفاده از توابع توزیع احتمال و روابط بین آن‌ها، فرم تابع توزیع پسین به صورت کاملاً ریاضیاتی بدست آید. رویکرد دیگر نیز برای حل چنین مسائلی وجود دارد و آن استفاده از زنجیرهای مارکوف (مفهومی در فرایندهای تصادفی)، و اجرای فرایند نمونه‌گیری از تابع توزیع پسین به تعداد دفعات بالا و تخمین فرم آن است. رویکرد دوم می‌تواند در مسائلی که رویکرد اول برای آن‌ها جوابی ندارد نیز مفید واقع شود.
- تحلیل رگرسیونی
تحلیل رگرسیونی به معنی مدلسازی رابطه‌ی بین مجموعه‌ای از متغیرهای پیشگو یا مستقل و متغیر پاسخ یا وابسته است. تحلیل رگرسیونی طیف وسیعی از مدل‌ها را دربرمی‌گیرد. به عنوان مثال رگرسیون خطی روشی برای مدلسازی رابطه‌ی خطی بین دو متغیر است. در رگرسیون خطی تلاش می‌شود تا با کمک مجموعه‌ای از متغیرهای پیشگو، متغیر پاسخ که مقدار حقیقی دارد را به وسیله‌ی یک خط راست تقریب زد. در مدل‌های پیچیده‌تر رگرسیونی این رابطه می‌تواند به فرم درجه دو و یا حتی پیچیده‌تر نیز باشد. در مدلسازی رگرسیونی تلاش می‌شود تا امید ریاضی متغیر هدف به کمک متغیرهای پیشگو با خطای کمی پیش‌بینی شود.
- روش حداقل مربعات معمولی
روش حداقل مربعات معمولی(OLS) به ما امکان می‌دهد که پارامترهای یک مدل رگرسیون خطی را تخمین بزنیم. هدف این روش تعیین یک مدل خطی است که مجموع مربعات خطا بین مشاهدات یک مجموعه داده و موارد پیش‌بینی شده توسط مدل را به حداقل برساند. در واقع در این روش، با فاصله گرفتن مقدار پیش‌بینی مدل از مقدار واقعی متغیر پاسخ، هزینه‌ای به اندازه‌ی مجذور این فاصله به مدل تحمیل می‌شود. این تابع خطا ویژگی‌های خوبی در مشتق‌گیری دارد و به طور کلی یک تابع هزینه‌ی معروف در ریاضیات است.
- ضریب همبستگی
ضریب همبستگی نوع و جهت رابطه‌ی بین دو متغیر را نشان می‌دهد. اگر ضریب همبستگی بیبن دو متغیر مثبت باشد، جهت رابطه‌ی دو متغیر مستقیم خواهد بود. به این معنی که با افزایش یکی، دیگری افزایش می‌یابد و با کاهش یکی، دیگری نیز کاهش می‌یابد. اما اگر ضریب همبستگی بین دو متغیر منفی باشد، رابطه‌بین دو متغیر به صورت عکس خواهد بود. یعنی با افزایش یکی، دیگری کاهش خواهد یافت.
با توجه به نوع هرکدام از دو متغیر، انواع مختلفی از ضرایب همبستگی معرفی می‌شوند. معروف‌ترین آن‌ها ضریب همبستگی پیرسونی است که برای سنجش ارتباط بین دو متغیر تصادفی پیوسته تعریف می‌شود.
ضریب همبستگی پیرسونی معیاری از رابطه‌ی خطی بین دو متغیر است که برای یک نمونهی تصادفی به صورت زیر تعریف می‌شود و مقداری بین 1+ و 1- می‌گیرد:
که در آن 
، 
، و 
به صورت زیر تعریف می‌شوند:
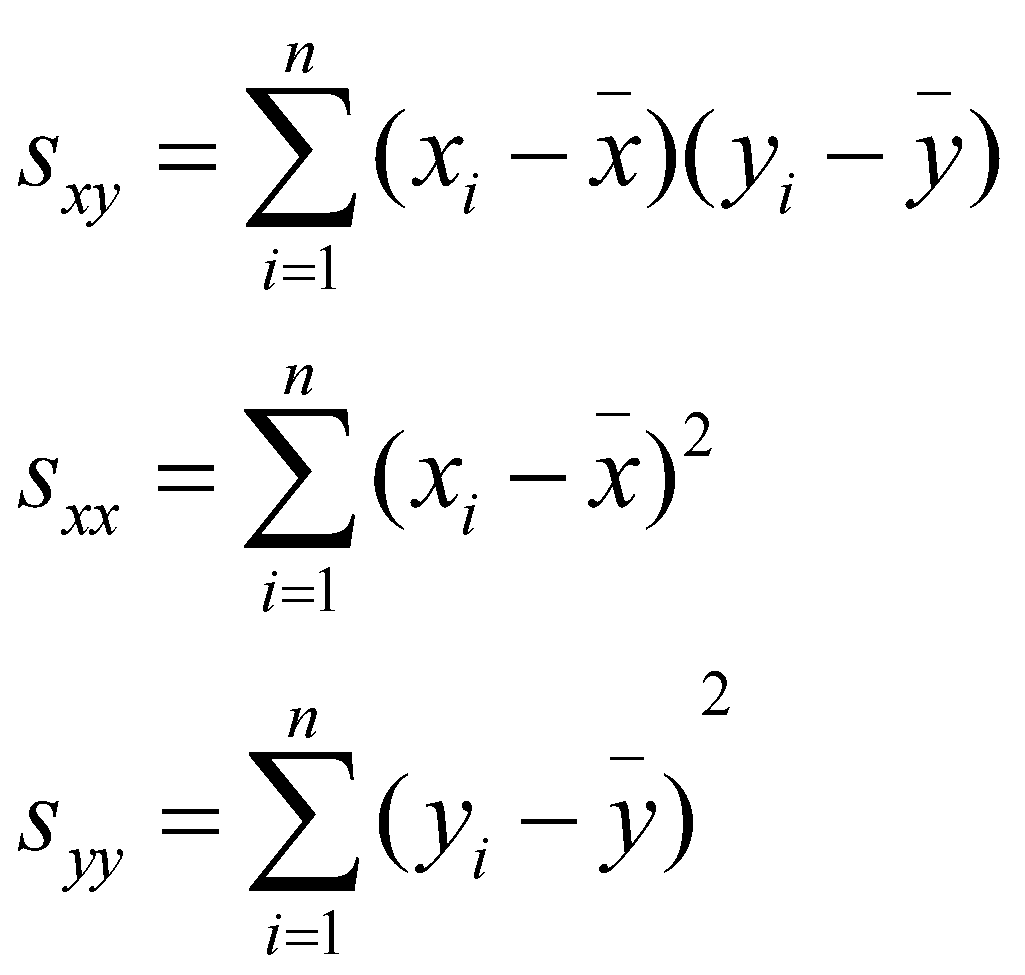
در واقع ضریب همبستگی پیرسونی، فاصله‌ی کسینوسی را بین بردارهایی که با میانگینشان مرکزی شده‌اند، محاسبه‌می‌کند.
- تجزیه‌ی واریانس
در کاربردهای عملی خیلی مواقع پیش می‌آید که بخواهیم میانگین یک متغیر تصادفی را در گروه‌های مختلف مقایسه کنیم. مثلا می‌خواهیم آزمون کنیم که آیا میانگین نمرات ریاضی یک کلاس از کلاس دیگر بالاتر راست یا نه. یا میزان آنتی‌بادی موجود در خون دو گروه واکسن‌زده و مبتلاشده به بیماری متفاوت است یا نه. برای اینگونه مسائل آزمون‌های مناسب آماری‌ای وجود دارند که نیاز ما با توجه به سطح خطای مورد نظرمان برطرف می‌کنند.
آنالیز واریانس (ANOVA) یک آزمون آماری برای آزمایش برابری میانگین داده‌ها در بین چند گروه مختلف است. ANOVA با مقایسه مجموع مربعات خطا در داخل و بین گروه‌ها، آزمون را به بیشتر از دو گروه تعمیم می‌دهد. آزمون نیز یک آزمون آماری است که برای مقایسه‌ی میانگین یک متغیر تصادفی در دو گروه مستقل کاربرد دارد. در هر آزمون آماری یک شاخص با نام "آماره‌ی آزمون" را محاسبه می‌کنیم. سپس توزیع احتمال آماره‌ی آزمون را می‌یابیم و با مقایسه‌ی مقدار آماره‌ی آزمون با چندک‌های مشخصی از توزیع آن، نسبت به نتیجه‌ی آزمون تصمیم می‌گیریم. در آزمون ، توزیع احتمال آماره‌ی آزمون، توزیع تی استیودنت است و در آزمون تجزیه‌ی واریانس، توزیع احتمال آماره‌ی آزمون، توزیع اف است.
- مثلثات
اگر چه مثلثات به نظریه‌ی احتمال ارتباطی ندارد و ما نیز قصد پرداختن به آن را در این مقاله نداریم، تصمیم گرفتیم تا یک یادآوری کوتاه در مورد نسبت‌های مثلثاتی زوایای پرکاربرد داشته باشیم. این زوایا در خیلی از مسائل مطرح می‌شوند و یک آشنایی مختصر در حد ریاضیات اوایل دوره‌ی دبیرستان با آن‌ها می‌تواند مفید باشد.
- نسبت‌های مثلثاتی
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
منظور از 
، تعریف‌نشده است.
- نمایش گرافیکی تابع sin و cos
در زیر یک نمایش گرافیکی از نحوه تغییر 
و 
با تغییر زاویه از 
به 
(یا به طور معادل از 
تا 
) نشان داده شده است. توجه داشته باشید که نمودار زیر یک دایره واحد (با شعاع 1) را نشان می‌دهد.
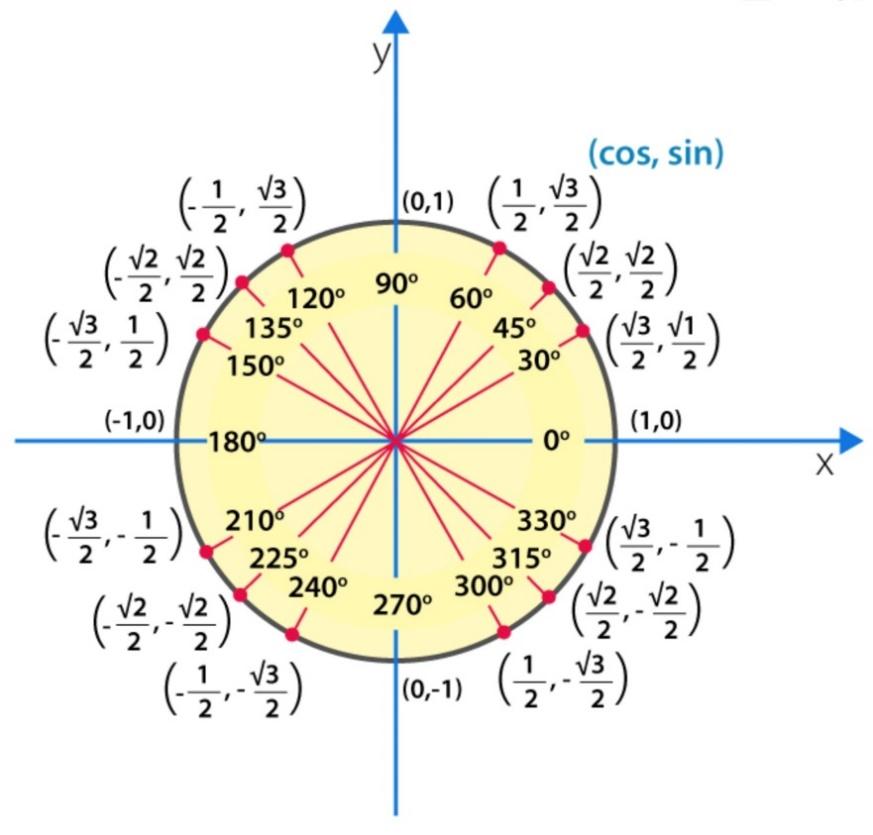
شکل 29: نمایش گرافیکی 
و 
روی دایره‌ی واحد
- منبع کمکی
https://aman.ai/primers/math/#correlation
نظرات