1. چکیده

در این پست، قصد داریم مفهوم‌های اساسی نظریه‌ی احتمال را به طور خلاصه معرفی کنیم. ابتدا، به توضیحی کلی درباره‌ی رویدادهای تصادفی و متغیرهای تصادفی پرداخته و سپس برخی از شاخص‌های آماری مانند امید ریاضی و واریانس را تعریف و توزیع‌های احتمالی مهم و پرکاربرد را معرفی می‌کنیم. در ادامه، مفاهیم آماری مانند رگرسیون خطی، ضریب همبستگی، تفاوت آماری فراوانی‌گرا و بیزی را توضیح می‌دهیم. این مفاهیم اساسی در تحلیل داده‌ها و انجام تحقیقات آماری بسیار مفید و کارآمد هستند. در پایان ، یک یادآوری از روابط ابتدایی مثلثاتی نیز ارائه شده است. این روابط در برخی از محاسبات و مسائل ریاضی به شما کمک می‌کنند و می‌توانند در فهم بهتر مفاهیم آماری و احتمالی نیز مفید باشند.

2. نظریه احتمال

1. مفاهیم

1. رخدادهای تصادفی

رخدادهای تصادفی در جهان پیرامون ما وجود دارند. نظریه احتمال چارچوبی ریاضیاتی است که به ما امکان می‌دهد رویدادهای تصادفی را به شیوه‌ای منطقی و صحیح، تجزیه و تحلیل کنیم. احتمال یک رویداد، عددی است که میزان احتمال وقوع آن رویداد را نشان می‌دهد. این عدد همواره بین 0 تا 1 است که صفر نشان‌دهنده‌ی عدم امکان وقوع و یک، نشان‌دهنده‌ی قطعیت وقوع است.

یک مثال کلاسیک از یک آزمایش احتمالی، پرتاب یک سکه‌ی سالم است که در آن دو برآمد ممکن، شیر یا خط هستند. در این حالت، احتمال مشاهده‌ی شیر یا خط،  است. در پرتاب مکرر سکه، ممکن است در ابتدا بیشتر یا کمتر از 50 درصد مواقع، روی شیر سکه را مشاهده کنیم. اما وقتی تعداد پرتاب‌ها زیاد شود، احتمال مشاهده شیر به 50 درصد نزدیک می‌شود. یعنی هر چقدر بیشتر پرتاب کنیم، نسبت شیر به تعداد کل پرتاب‌ها به 50 درصد می‌رسد.

در مورد یک سکه ناسالم، دو برآمد به یک اندازه محتمل نیستند؛ بنابراین، برای تعیین وزن مناسب برای هر یک از برآمدها (مثلاً 1 برای شیر و 0 برای خط) باید اقدام کنیم. با این کار، یک مفهوم ریاضی را ایجاد می‌کنیم که به آن «متغیر تصادفی» می‌گوییم. به این معنا که مقادیر مختلف این متغیر (شیر و خط) با احتمالات مختلفی اتفاق می‌افتند و ما برای هر کدام وزنی تعیین می‌کنیم.

2.  امید ریاضی

"امید ریاضی" یک مفهوم در احتمالات و آمار است که می‌توان آن را به سادگی به عنوان میانگین یا مرکز ثقل توزیع متغیر تصادفی تفسیر کرد. به اصطلاح، این عدد نمایانگر میانگینی است که از مقادیر متغیر تصادفی در نمونه‌های مستقل مختلفی که از توزیع داده شده انتخاب می‌شود، محاسبه می‌گردد. برای دقت بیشتر، تعریف امید ریاضی به صورت معادل مجموع ضرب همه مقادیر ممکن در دامنه متغیر تصادفی است، که هر کدام با احتمال مربوط به خودشان وزن‌دار شده‌اند. به این ترتیب، امید ریاضی متغیر تصادفی به ما اطلاع می‌دهد که در انتظار چه مقداری از متغیر تصادفی هستیم.

آزمایش احتمالی پرتاب یک تاس سالم را در نظر بگیرید. پس از تعداد زیادی تکرار آزمایش، میانگین نمونه‌ای اعداد مشاهده‌شده‌ی آزمایش در حال اجرا به مقدار امید ریاضی آن (3.5) همگرا می‌شود. یعنی اگر بین اعداد مشاهده شده‌ی روی تاس میانگین بگیرید، عددی در حدود 3.5 مشاهده خواهید کرد. تغییر ساختار تاس مورد استفاده (غیرعادلانه کردن تاس) بر مقدار امید ریاضی توزیع اعداد مشاهده شده، تأثیر می‌گذارد.

3. واریانس

در حالی که امید ریاضی معیاری از تمرکز توزیع احتمال را ارائه می‌دهد، واریانس یک متغیر تصادفی، میزان پراکندگی توزیع متغیر تصادفی را به صورت کمّی بیان می‌کند. واریانس، برابر با میانگین مجذور اختلاف بین متغیر تصادفی و امید ریاضی آن است.

اگر به طور تصادفی از یک دسته‌ی ده‌تایی که از 1 تا 10 شماره‌گذاری شده‌اند کارت بکشید، متوجه خواهید شد که میانگین مجذور اختلافات، شروع به شبیه شدن به مقدار واقعی واریانس می‌کند.

4. نظریه مجموعه‌ها

مجموعه، به طور کلی گردایه‌ای از اشیاء است. در زمینه‌ی نظریه احتمال، از نماد مجموعه برای مشخص‌کردن حالات ممکن متغیر تصادفی استفاده می‌کنیم. برای مثال، می‌توانیم رویداد مشاهده‌ی «یک عدد زوج» را با مجموعه {2،4،6} نمایش دهیم. به همین دلیل، آشنایی با جبر مجموعه ها مهم است. منظور از جبر مجموعه‌ها در اینجا عملگرهای ساده‌ی تعریف‌شده بین مجموعه‌ها مانند اجتماع و اشتراک هستند. مجموعه‌ها معمولاً به کمک نمودارهای ون ترسیم می‌شوند.

نظریه‌ی مجموعه‌ها شاخه‌ای از ریاضیات است که در آن پدیده‌های جهان و اشیاء ریاضی به کمک مجموعه‌ها بیان می‌شوند. تمامی مفاهیمی که در جهان ریاضیات می‌شناسیم مانند تابع، مشتق، انتگرال و ... تماما به کمک نظریه‌ی مجموعه‌ها معرفی می‌شوند. در فضای آمار و احتمال با خود نظریه‌ی مجموعه‌ها به صورت مشخص کاری نداریم اما وقتی می‌خواهیم برآمدهای ممکن فضای پیشامد یک آزمایش تصادفی را در حالت گسسته مشخص کنیم از نمادگذاری مربوط به مجموعه‌ها کمک می‌گیریم. به عنوان مثال برای نمایش دادن نتایج آزمایش پرتاب سکه، از مجموعه‌ی "شیر" و "خط" استفاده می‌کنیم.

5. شمارش

شمارش تعداد دنباله‌ها یا مجموعه‌هایی که شرایط خاصی را برآورده می‌کنند، می‌تواند به طرز شگفت‌آوری دشوار باشد. به عنوان مثال، کیسه‌ای از تیله‌ها را در نظر بگیرید که در آن هر تیله رنگ متفاوتی دارد. اگر چهار تیله در کیسه وجود داشته باشد و تیله‌ها را یکی‌یکی و بدون جایگذاری از کیسه بیرون بکشیم، چند ترتیب مختلف (جایگشت) از تیله‌ها ممکن است؟ چند مجموعه‌ی مختلف (ترکیب) برای برداشت چهارتایی از کیسه، 24 جایگشت متفاوت وجود دارد اما تنها یک ترکیب از تیله‌ها ممکن است (هر چهار تیله در خروجی خواهند بود).

6. احتمال شرطی

 احتمالات شرطی به ما این امکان را می‌دهند که با در نظر گرفتن اطلاعات موجود در مورد سیستم مورد بررسی، محاسبات دقیق‌تری انجام دهیم. به عبارت دیگر، از طریق احتمالات شرطی، می‌توانیم احتمال وقوع یک حادثه را با توجه به شرایط خاصی که داریم، محاسبه کنیم. به عنوان مثال، اگر امروز هوا ابری باشد، احتمال بارش باران در روز آینده ممکن است بیشتر باشد تا حالتی که امروز هوا صاف باشد. اینجا احتمال بارش باران در آینده به شرطی است که امروز هوا ابری باشد؛ به عبارت دیگر، محاسبات احتمالاتی ما با توجه به اطلاعات شرطی انجام می‌شود که در دسترس داریم و این اطلاعات به ما کمک می‌کنند تا پیش‌بینی‌ها و محاسبات دقیق‌تری داشته باشیم.

از منظر ریاضیاتی، محاسبه‌ی یک احتمال شرطی به معنای محدودکردن فضای نمونه به یک رویداد خاص است. بنابراین در مثال باران، به جای اینکه به طور کلی به تعداد دفعات بارندگی در هر روز نگاه کنیم، تصور می‌کنیم که فضای نمونه ما فقط شامل روزهایی است که روز قبل آن ابری بوده است. سپس تعیین می کنیم که چند روز از آن روزها بارانی بوده است و بدین ترتیب احتمال شرطی مورد نظر را برآورد می‌کنیم.

2. توزیع‌های احتمال

توزیع احتمال، احتمال نسبی تمام برآمدهای ممکن را مشخص می‌کند. قبل از اینکه به معرفی چند توزیع احتمال رایج و معروف بپردازیم، اصطلاحات مرتبط با توزیع‌های احتمال را مرور می‌کنیم.

7. متغیرهای تصادفی

به طور رسمی، متغیر تصادفی تابعی است که به هر برآمد آزمایش در فضای احتمالاتی، یک عدد حقیقی را اختصاص می‌دهد. با نمونه‌گیری و انجام آزمایش‌های تصادفی مرتبط با توزیع احتمال خود، می‌توانید توزیع تجربی متغیر تصادفی خود را به دست آورید. یعنی می‌توانید توزیع مربوط با آزمایش تصادفی خود را تخمین بزنید.

8. قضیه‌ی حد مرکزی

قضیه‌ی حد مرکزی (CLT) بیان می‌کند که میانگین نمونه‌‌ی به اندازه‌ی کافی بزرگ از متغیرهای تصادفی مستقل و هم‌توزیع، تقریباً به طور نرمال توزیع شده است. منظور از متغیر تصادفی مستقل، متغیرهایی هستند که احتمال رخداد هم‌زمان آن‌ها، برابر با ضرب احتمال رخداد‌های منفرد آن‌هاست. به عبارت ساده‌تر، رخ دادن یکی از آن‌ها، بر روی احتمال رخداد دیگری تاثیری ندارد. منظور از متغیر تصادفی هم‌توزیع، متغیر‌هایی هستند که  دقیقا از یک توزیع احتمال با پارامترهای یکسان پیروی می‌کنند. بنابراین و براساس این قضیه، فرقی نمی‌کند متغیرهای تصادفی شما از چه توزیع‌ احتمالی پیروی می‌کنند، صرفا اگر مستقل و هم‌توزیع باشند، میانگین آن‌‎ها به توزیع نرمال میل خواهد کرد. هرچه حجم نمونه بزرگتر باشد، این تقریب بهتر است.

3. انواع توزیع احتمال

دو دسته توزیع احتمال وجود دارد: گسسته و پیوسته. توجه داشته باشید که توزیع‌های گسسته با تابع جرم احتمال(PMF)   تعریف می‌شوند در حالی که توزیع‌های پیوسته با تابع چگالی احتمال  (PDF) تعریف می‌شوند، در بخش‌های بعدی راجع به آن‌ها توضیح بیشتری ارائه خواهیم داد.

گسسته

یک متغیر تصادفی گسسته، دارای تعداد متناهی یا قابل شمارش مقادیر قابل اختیار است. اگر 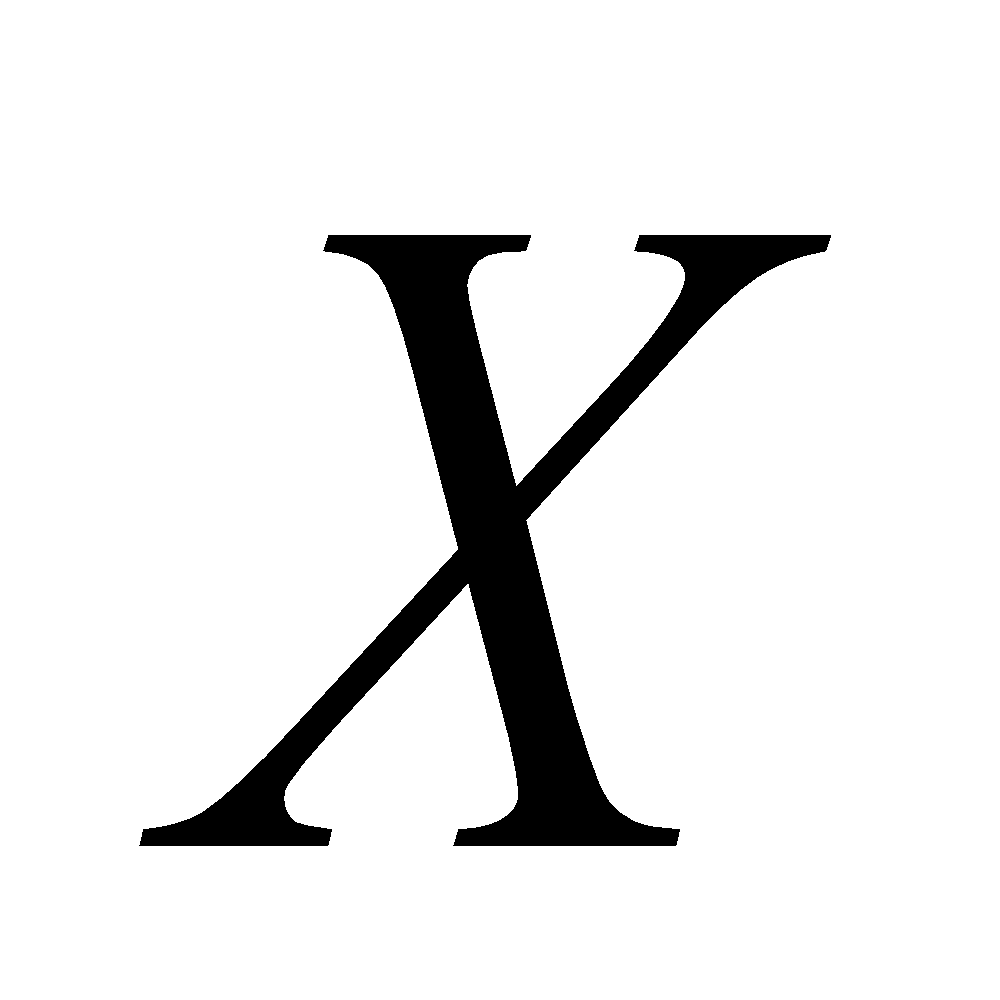 یک متغیر تصادفی گسسته باشد، توابع غیر منفی یکتای و  وجود دارد، به طوری که در روابط زیر صدق می‌کنند:

که در آن،  نشان‌دهنده‌ی تابع جرم احتمال و  نشان‌دهنده‌ی تابع توزیع تجمعی است.

پیوسته

یک متغیر تصادفی پیوسته تعداد ناشمارا و نامتناهی از مقادیر ممکن (مثلاً همه اعداد حقیقی) را اختیار می‌کند. اگر 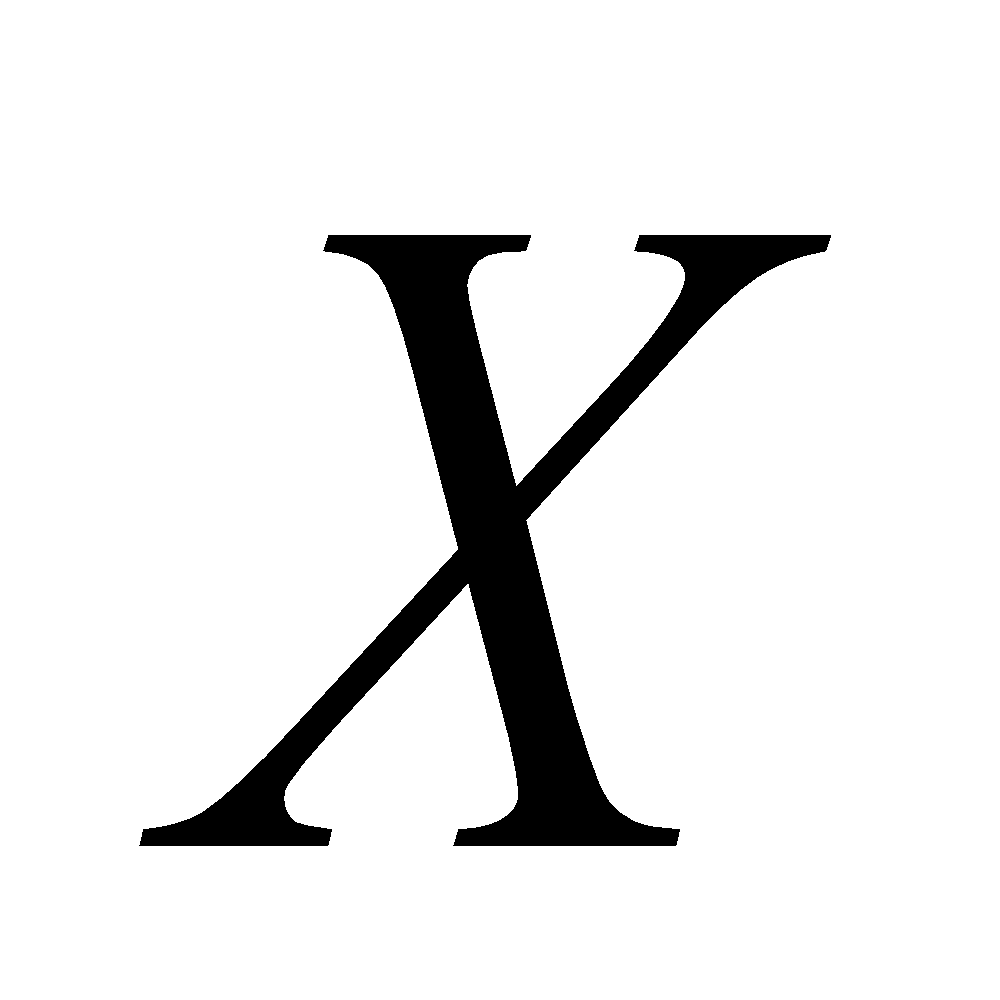 یک متغیر تصادفی پیوسته باشد، توابع غیر منفی یکتای  و  وجود دارند که در روابط زیر صدق می‌کنند:

که در آن،  نشان‌دهنده‌ی تابع چگالی احتمال  (PDF)و  نشان‌دهنده‌ی تابع توزیع تجمعی (CDF)  است.

9. توزیع برنولی

توزیع برنولی در آزمایش با خروجی باینری ایجاد می‌شود. به همین دلیل است که از آن برای مدل‌سازی داده‌های باینری استفاده می‌شود. مانند ساختن یک دسته‌بندی‌کننده باینری تشخیص هرزنامه، یا مدل‌سازی پرتاب سکه. بنابراین یک متغیر تصادفی برنولی یک توزیع احتمال گسسته را مدل می‌کند. متغیر تصادفی برنولی مقادیر یک و صفر را به ترتیب با احتمال  و  می‌پذیرد. میانگین متغیر تصادفی برنولی  و واریانس آن برابر است. 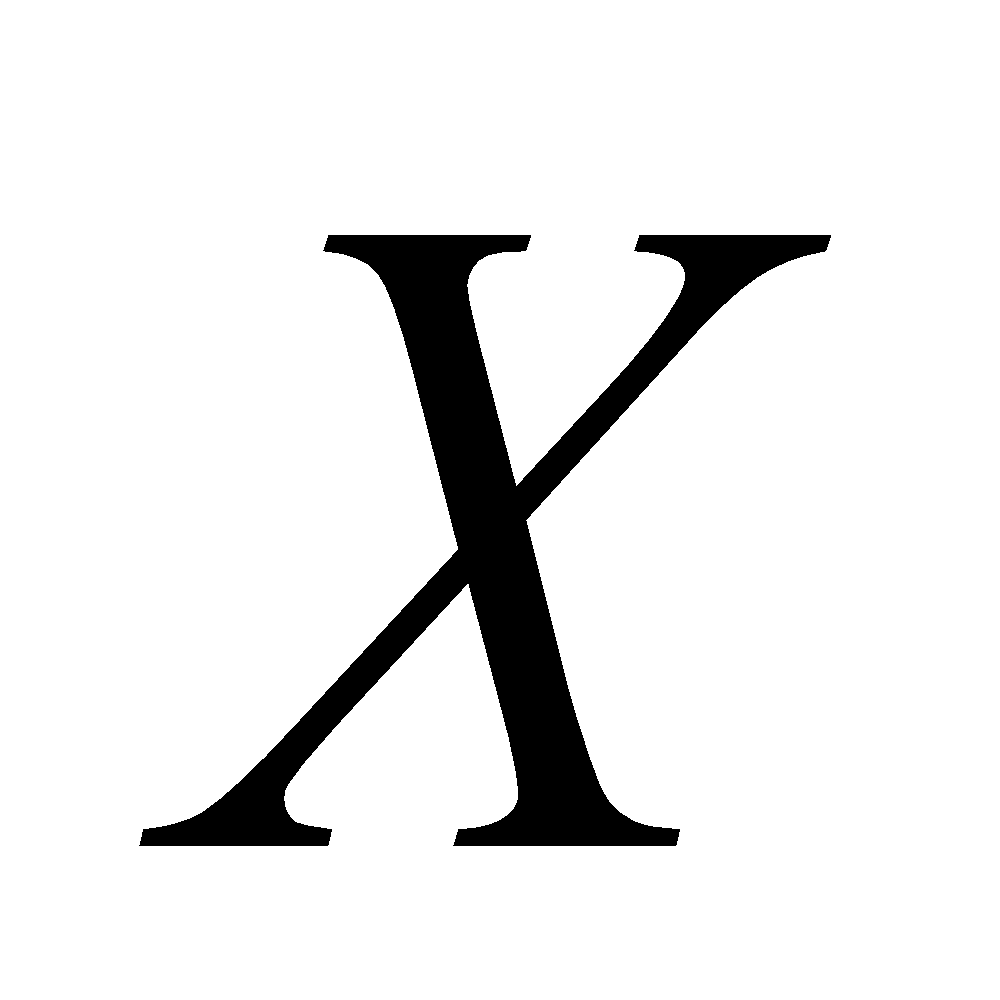اگر  یک متغیر تصادفی برنولی باشد، معمولاً را «موفقیت» و را «شکست» می‌نامیم.

تابع جرم احتمال یک توزیع برنولی، به صورت زیر است:

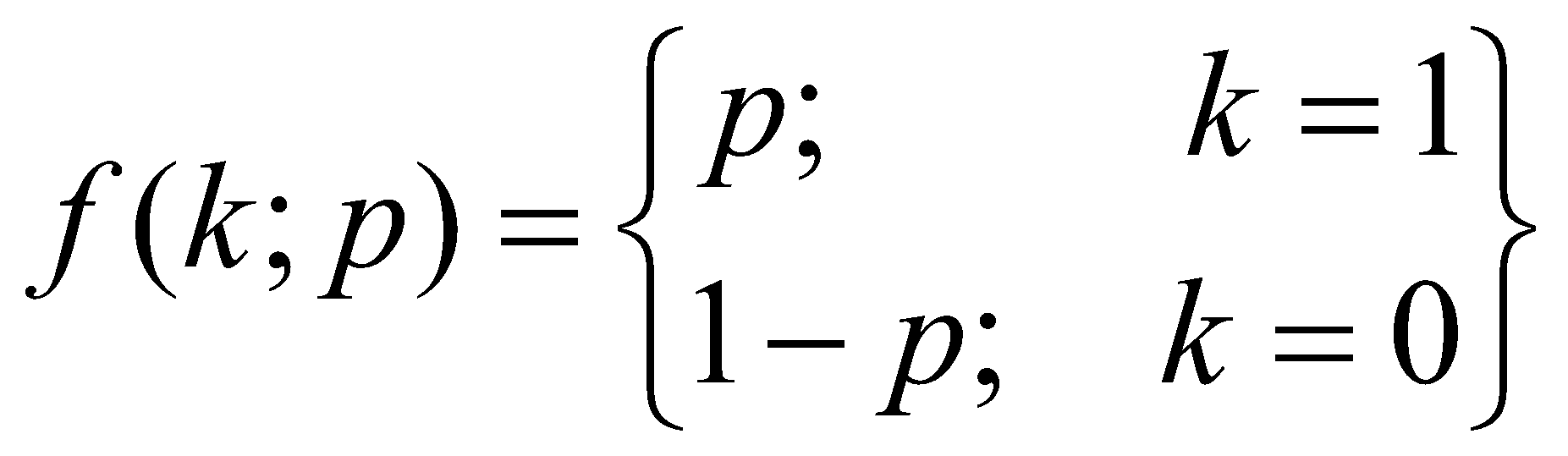
یا به عبارت دیگر:

یا:

اگر  آزمایش برنولی مستقل با شانس پیروزی برابر با هم انجام شوند، به توزیع حاصل از آن، توزیع احتمال دوجمله‌ای می‌گوییم؛ بنابراین توزیع برنولی، حالت خاصی از توزیع دوجمله‌ای است.

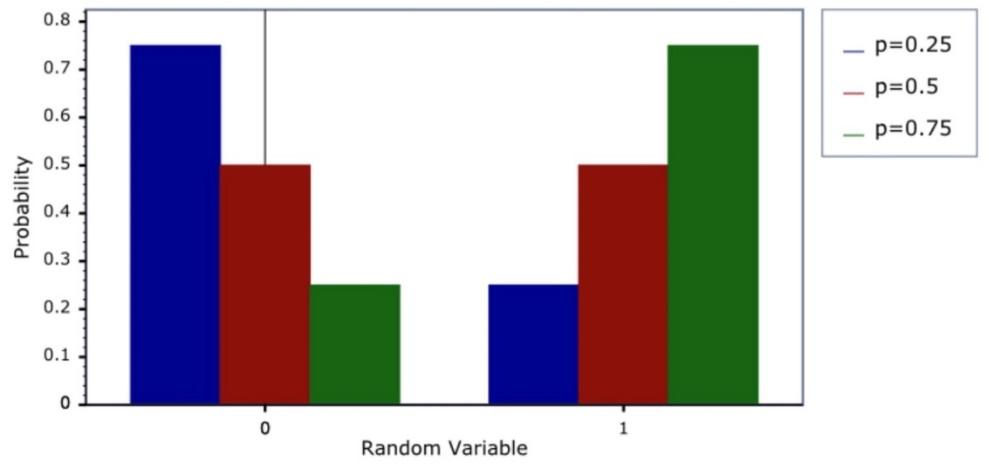
شکل 14: نمودار جرم احتمال توزیع برنولی به ازای مقادیر مختلف شانس پیروزی

تابع توزیع تجمعی برای توزیع برنولی به صورت زیر است:

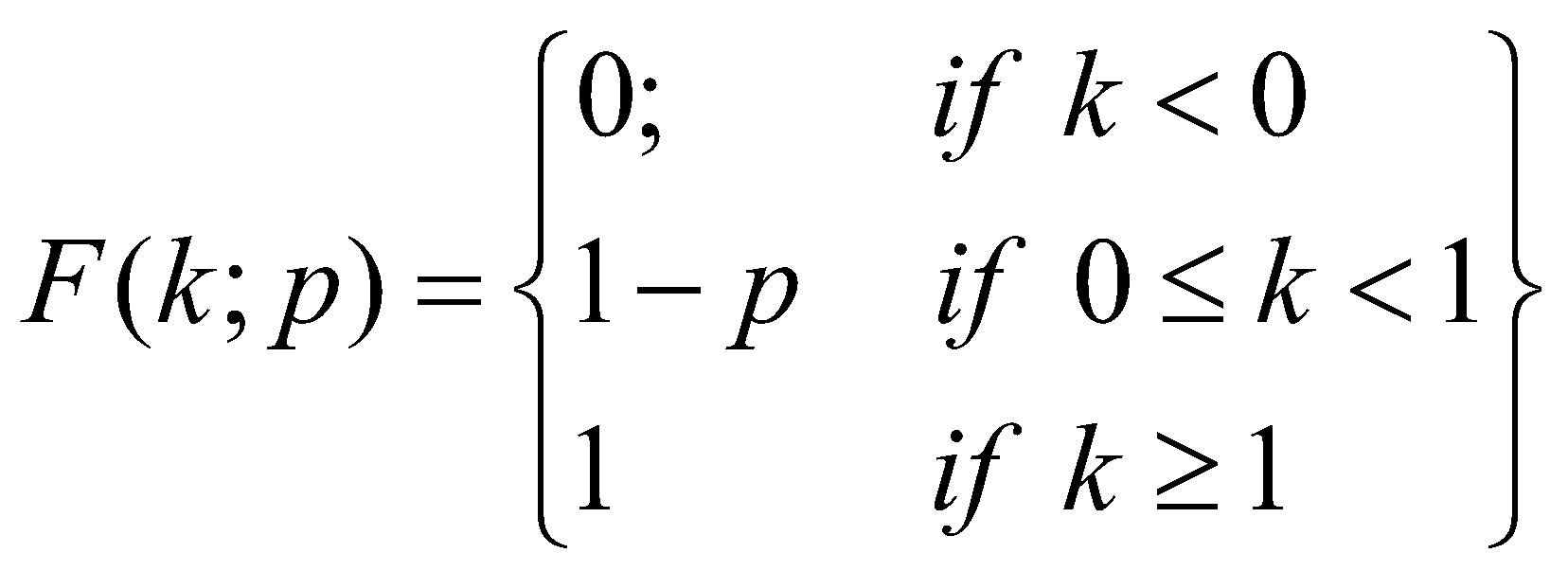
در شکل‌های 14 و 15 نمودار جرم احتمال و توزیع تجمعی توزیع برنولی به ازای مقادیر مختلف پارامتر نمایش داده شده است.         

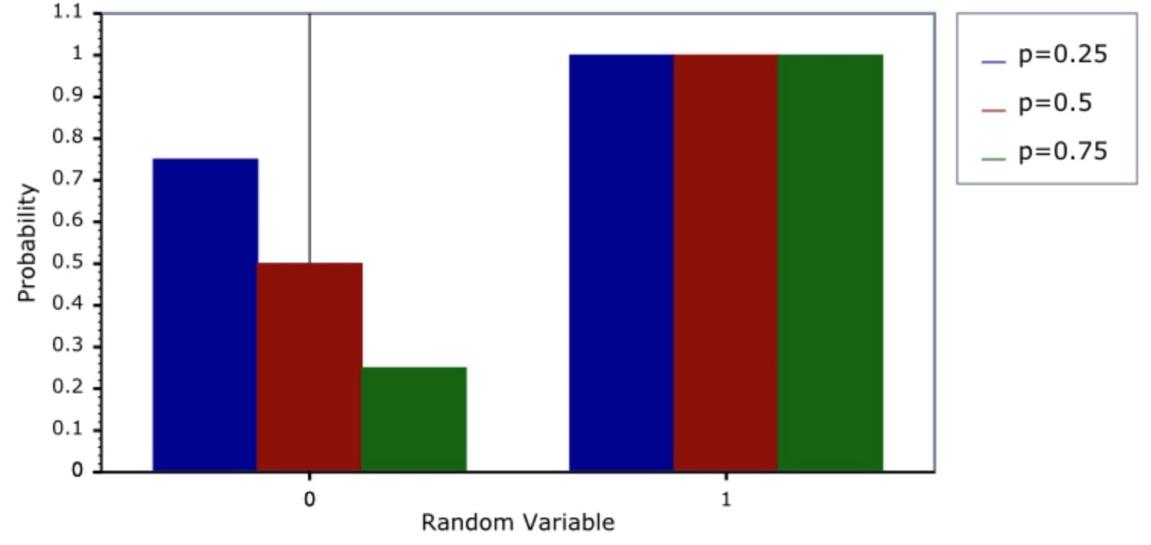
شکل 15: نمودار تابع توزیع تجمعی توزیع برنولی در نقاط صفر و یک به ازای مقادیر مختلف شانس پیروزی

آزمایش نمونه‌های مستقل و هم‌توزیع برنولی

اگر مجموعه‌ای از مشاهدات مستقل و هم‌توزیع برنولی  مشاهده شوند، تابع likelihood (تابع احتمالی که ورودی آن نمونه‌ی تصادفی است و خروجی آن، احتمال مناسب بودن پارامترهای توزیع است) به صورت زیر است:

دقت داشته باشید که تابع احتمال، یک توزیع احتمال را به همراه پارامترهایش فرض می‌کند و به ازای هر نمونه‌ی تصادفی، یک مقدار احتمال یا شانس را به آن نظیر می‌کند. در صورتی که تابع likelihood، نمونه‌های تصادفی را به عنوان نمونه‌های مشاهده‌شده مفروض می‌گیرد و به ازای یک توزیع احتمال مشخص اما با پارامترهای نامعلوم، شانس اینکه نمونه‌های مشاهده‌شده از یک توزیع با مقادیر مختلف پارامتر آمده باشند را بیان می‌کند و likelihood فقط به  بستگی دارد. از آنجایی که  ثابت است و شناخته شده فرض می‌شود، می‌توان گفت که نسبت نمونه‌ای  حاوی تمام اطلاعات مربوط به  است. می‌توانیم تابع likelihood را نسبت بهبیشینه کنیم تا تخمین حداکثر درستنمایی را برای  به دست بیاوریم. اگر این کار را انجام دهید به این نتیجه خواهید رسید:

10. آزمایش دوجمله‌ای

متغیر تصادفی دوجمله‌ای از مجموعه‌ای از آزمایش‌های مستقل و هم‌توزیع برنولی به دست می‌آید. در نظر بگیرید که  نمونه‌های مشاهده شده‌ی مستقل و هم‌توزیع از توزیع برنولی هستند، آنگاه یک متغیر تصادفی دوجمله‌ای است. تابع جرم احتمال توزیع دوجمله‌ای به صورت زیر است:

نماد  (بخوانید انتخاب از )، تعداد انتخاب‌های ممکن  شیء از  شیء متمایز را نشان می‌هد و رابطه‌ی  محاسبه‌ی آن به صورت زیر است:

توجه داشته باشید که  و  را برابر با 1 در نظر می‌گیریم.

درک بهتر توزیع دوجمله‌ای

احتمال مشاهده‌ی 6 شیر از 10 پرتاب یک سکه با احتمال موفقیت  را در نظر بگیرید. احتمال مشاهده‌ی 6 شیر و 4 خط بدون در نظر گرفتن ترتیبی خاص، برابر 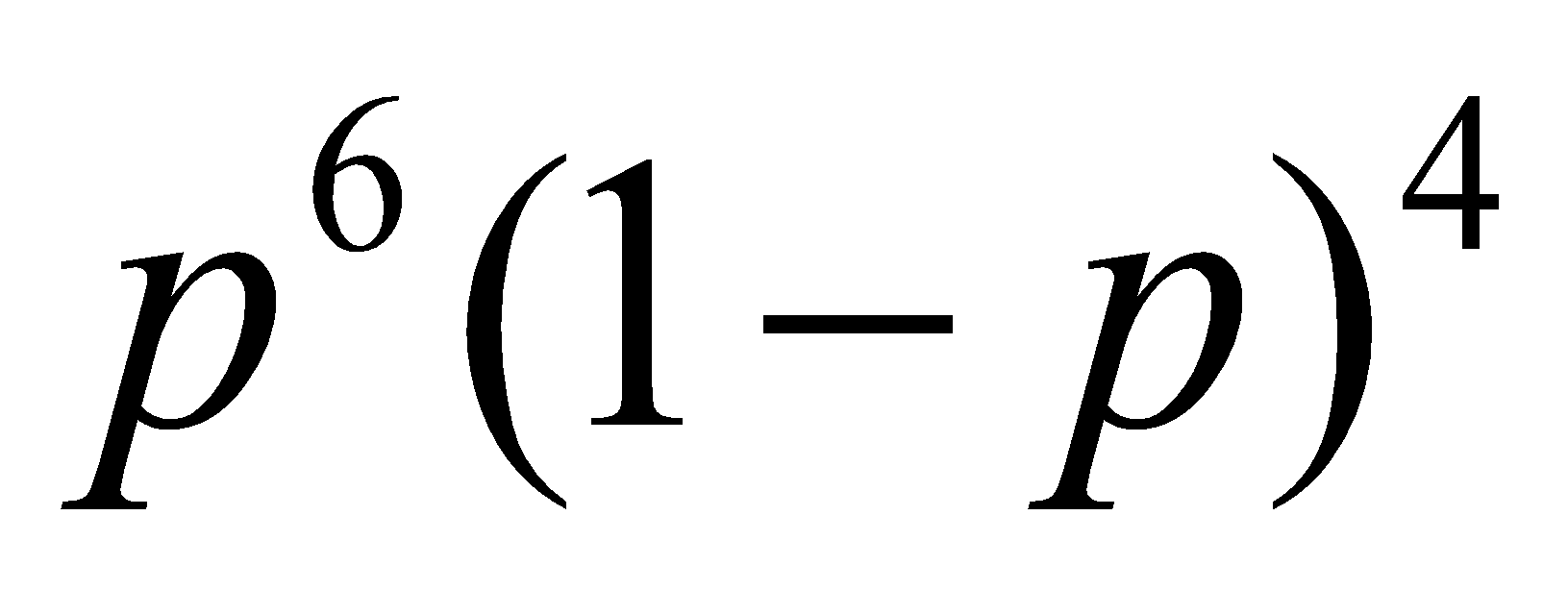است. دقت کنید که به تعداد  ترتیب مختلف برای مشاهده‌ی 6 شیر و 4 خط وجود دارد. حالا می‌توانید فرمول تابع جرم احتمال توزیع دوجمله‌ای را بهتر درک کنید.

برای مثال اگر هر جنسیت برای هر تولد به صورت مستقل 50 درصد احتمال داشته باشد، احتمال اینکه از 8 متولد، 7 تا یا بیشتر آن‌ها دختر باشد چقدر است؟

باید احتمال اینکه 7 یا 8 فرزند از کل 8 فرزند، دختر باشند را محاسبه کنیم. برای این کار متولد شدن دختر را پیروزی و متولد شدن پسر را شکست تلقی‌می‌کنیم. بنابراین با استفاده از تابع جرم احتمال توزیع دوحمله‌ای خواهیم داشت:

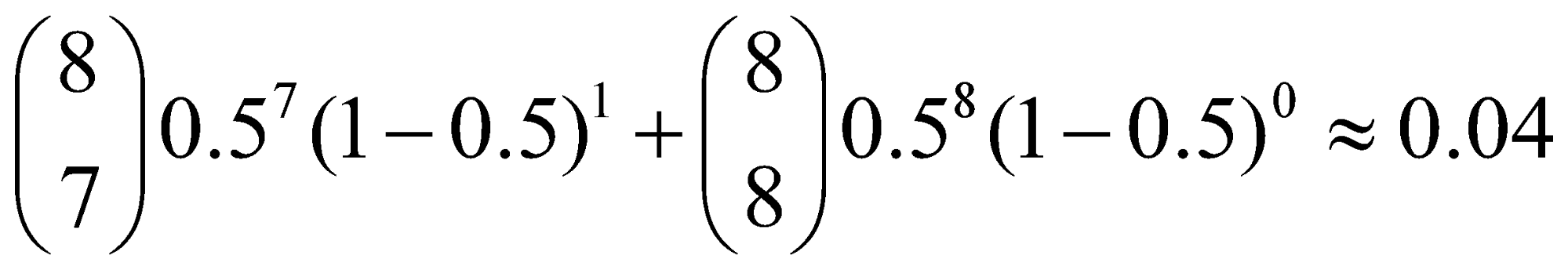
نمونه کد محاسبه در پایتون

تابع comb  از کتابخانه‌ی  math برای محاسبه‌ی جایگشت استفاده می‌شود. مسئله‌ی بالا در پایتون به صورت زیر است:

11. توزیع نرمال (گاوسی)

توزیع نرمال (گاوسی) تابع چگالی احتمال زنگوله‌ای شکل دارد و برای مدل‌سازی متغیرهای تصادفی دارای ‌مقدار حقیقی استفاده می‌شود. بسیاری از متغیرهای تصادفی در طبیعت مانند قد و وزن انسان‌ها از این توزیع پیروی می‌کنند؛ به همین دلیل است که به این توزیع، نرمال می‌گویند. به عنوان مثال، می‌توان از توزیع نرمال برای مدل‌سازی قد افراد استفاده کرد، زیرا می‌توان قد را نتیجه‌ی بسیاری از عوامل ژنتیکی و محیطی کوچک فرض کرد. یک مثال دیگر، مدل‌سازی قیمت خانه است زیرا قیمت یک خانه را می‌توان تابعی از مساحت، منطقه‌ی مدرسه، فاصله تا نقاط دیدنی و غیره فرض کرد. اگر 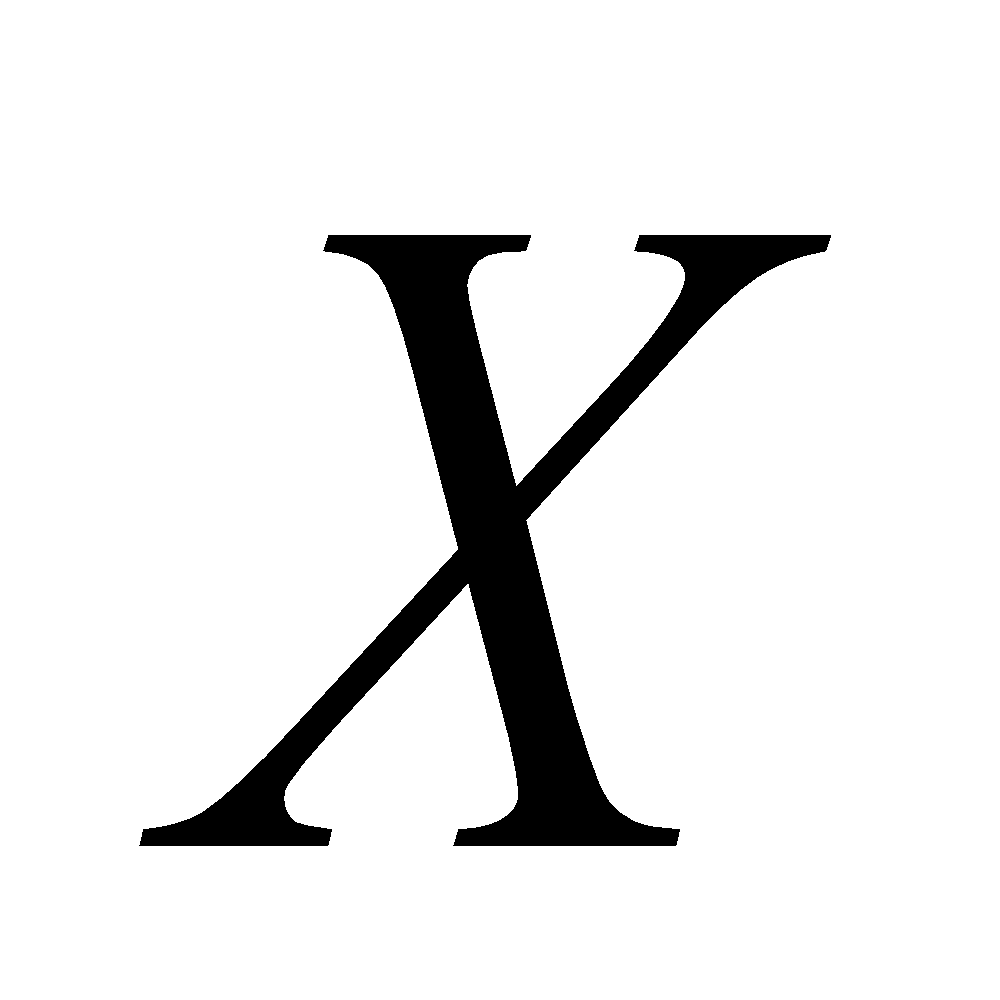یک متغیر تصادفی با توزیع نرمال باشد، داریم:

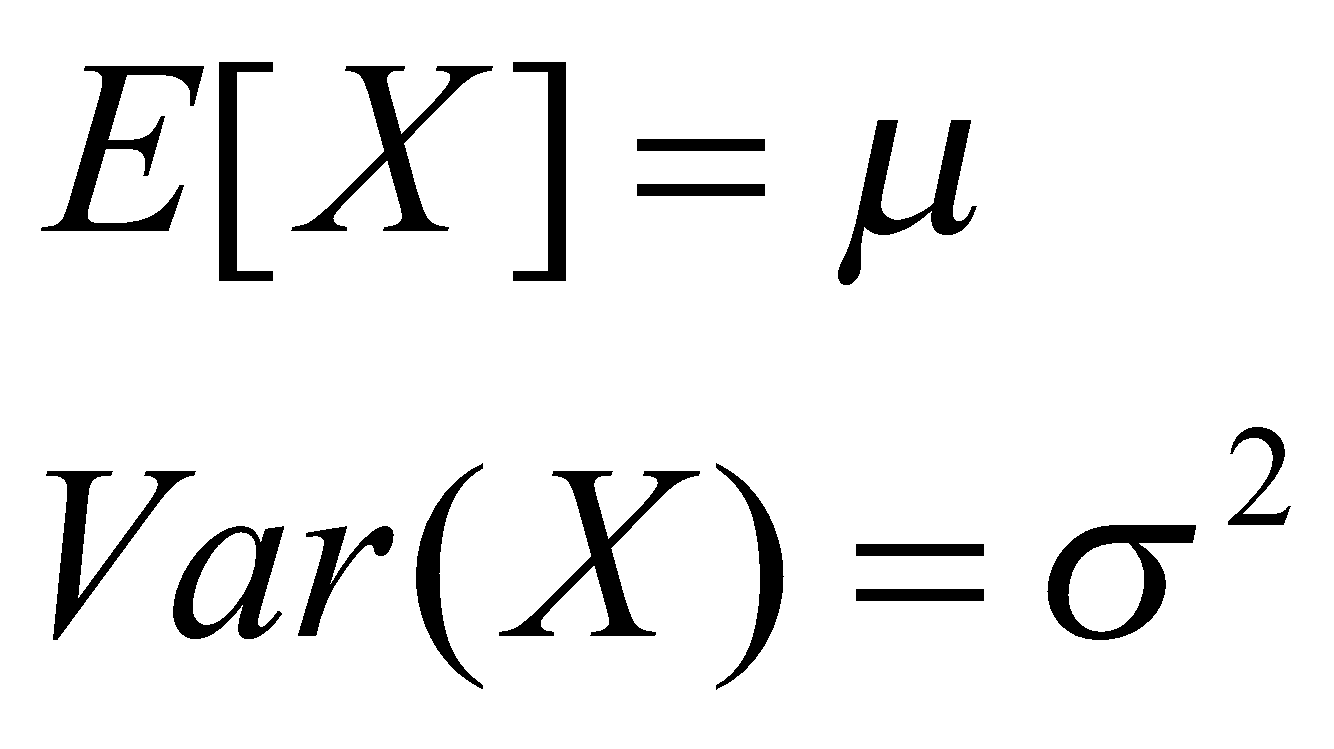
نماد مورد استفاده برای نشان‌دادن اینکه یک متغیر تصادفی از یک توزیع نرمال نمونه‌گیری شده است، به صورت زیر است:

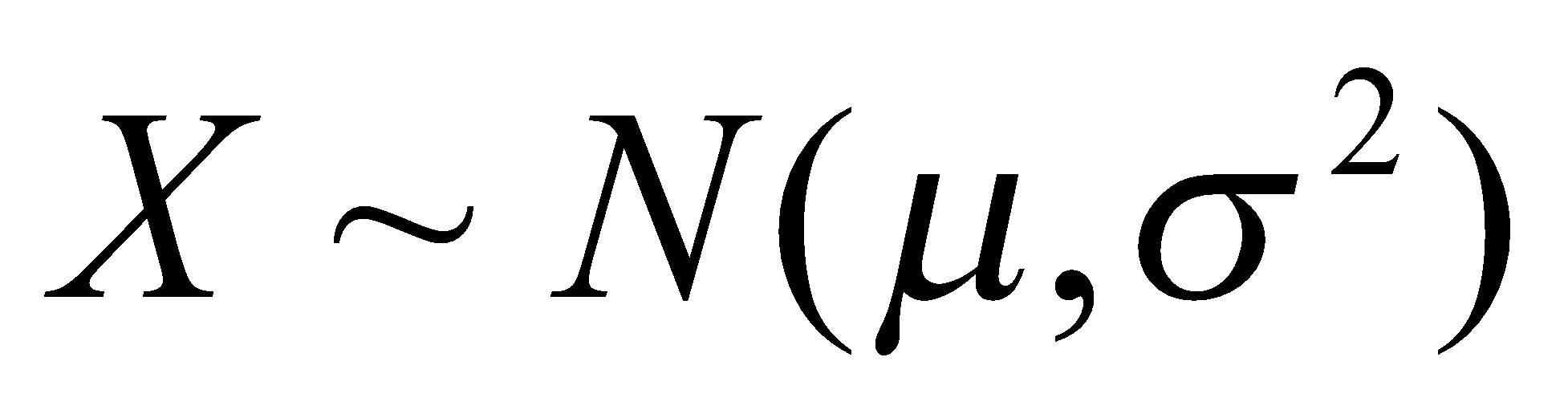
تابع چگالی احتمال یک متغیر تصادفی نرمال با میانگین   و واریانس  به صورت زیر است:

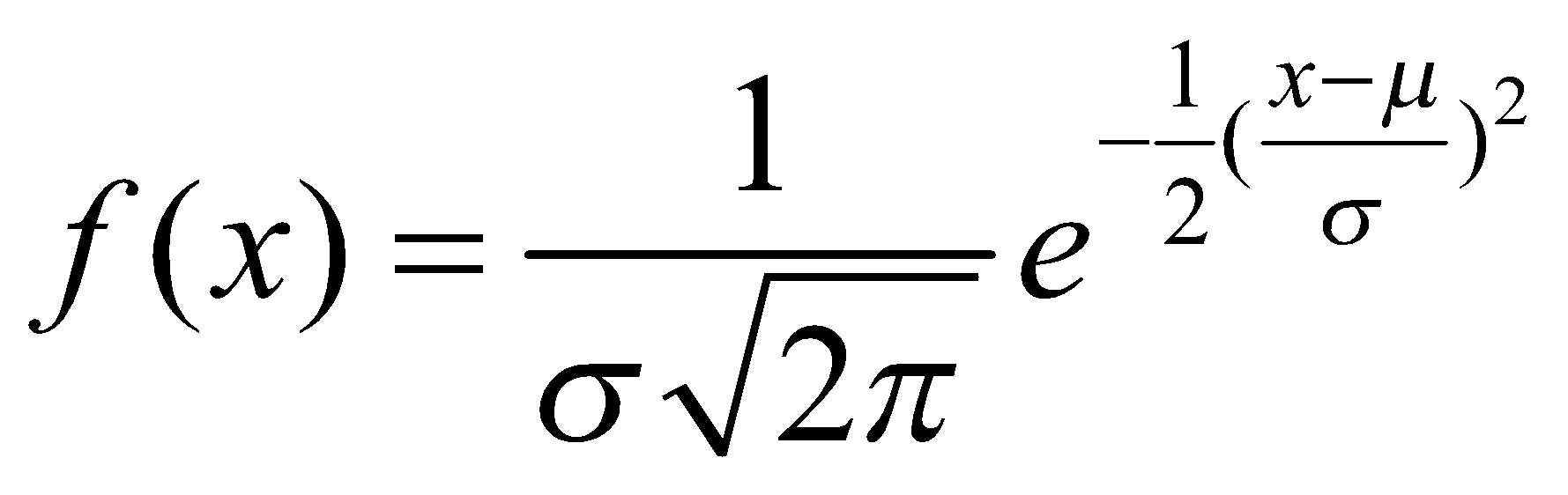
در شکل‌های 16 و 17 نمودار تابع چگالی و توزیع تجمعی توزیع نرمال را به ازای پارامترهای مختلف مشاهده می‌کنید.

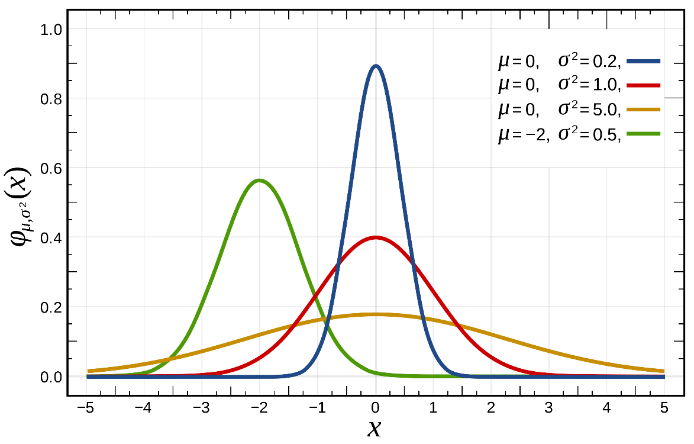
شکل 16: نمودار چگالی احتمال توزیع نرمال به ازای مقادیر مختلف میانگین و واریانس

تابع توزیع تجمعی توزیع نرمال به صورت زیر است:

که در آن منظور از ، تابع توزیع تجمعی نرمال استاندارد () است و ، تابع خطا را نمایش می‌دهد.

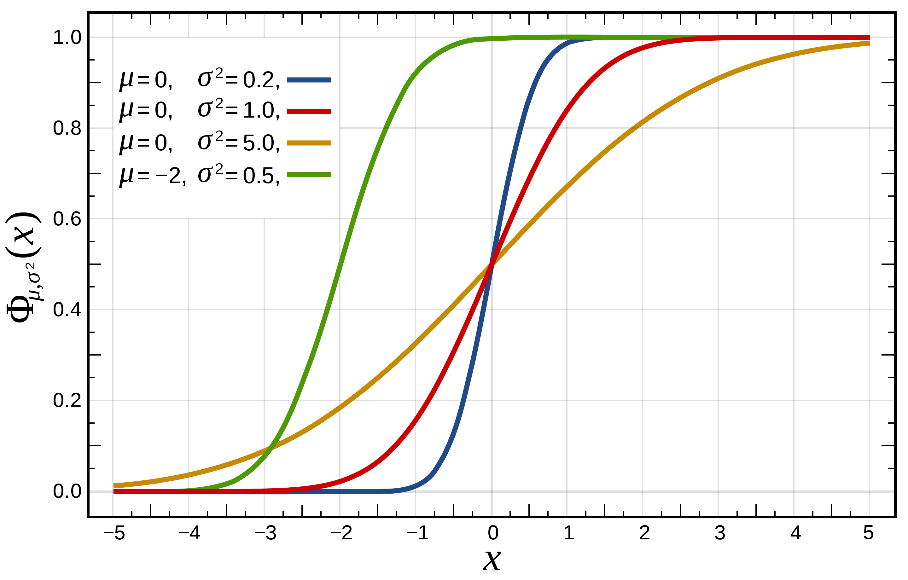
شکل 17: نمودار تابع توزیع تجمعی نرمال به ازای مقادیر مختلف و 

12. توزیع نرمال استاندارد

ساده‌ترین حالت توزیع نرمال، زمانی است که پارامتر میانگین آن برابر صفر و پارامتر واریانس آن برابر یک باشد:

به یاد داشته باشید که تابع چگالی احتمال توزیع نرمال استاندارد را با  نمایش می‌دهند. متغیرهای تصادفی که از این توزیع پیروی می‌کنند را با  نمایش می‌دهیم. در ادامه چند مثال را توضیح می‌دهیم.

مثال یک)

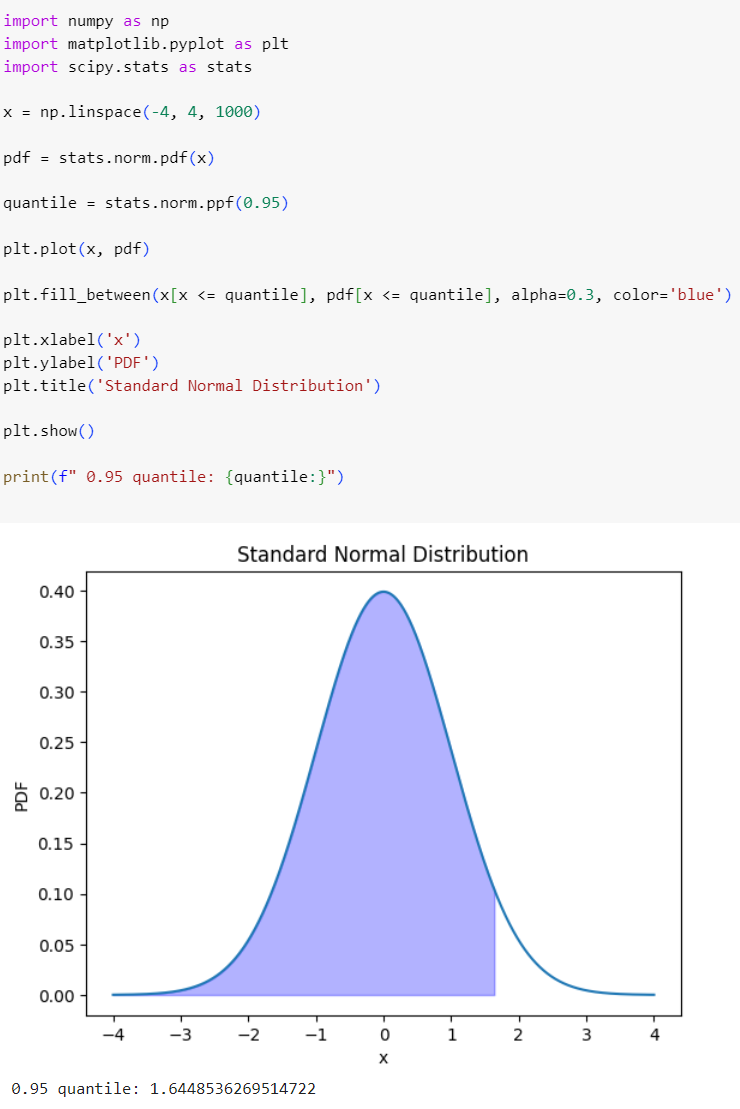
نقطه‌ای را در توزیع  بیابید که 95 درصد چگالی احتمال پشت آن باشد (به این نقطه، چندک 0.95 توزیع می‌گوییم).

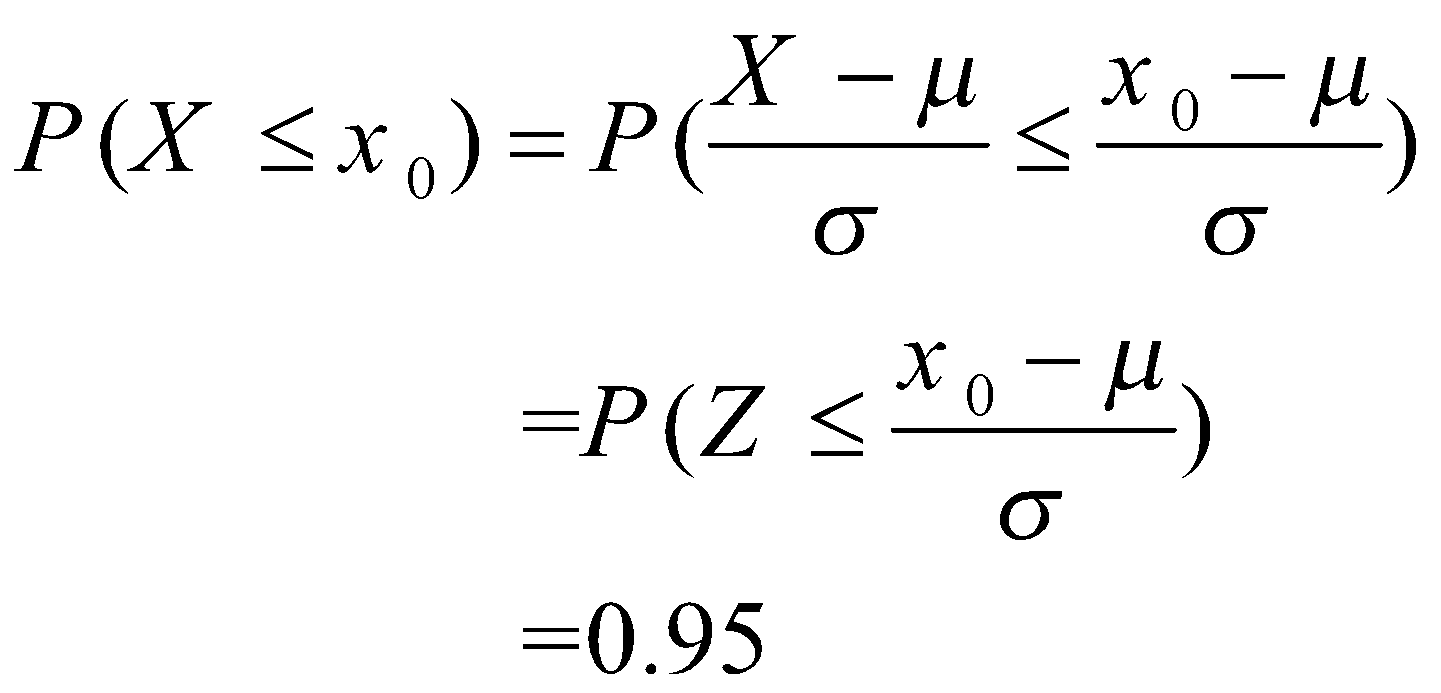
می‌دانیم که در توزیع نرمال استاندارد،  پس داریم: . به صورت کلی برای یافتن چندک توزیع نرمال داریم: که در آن،  چندک توزیع نرمال استاندارد است.

در قطعه کد زیر 1000 نقطه در بازه‌ی 4- تا 4+ تولید کردیم و میزان چگالی احتمال در هر کدام از نقاط به دست آوردیم. سپس به کمک متد ppf، چندک 0.95 توزیع نرمال استاندارد را به دست آوردیم و چاپ نمودیم.

همچنین نمودار چگالی احتمال توزیع نرمال استاندارد را نیز رسم کردیم و محل قرارگیری چندک 0.95 را روی محور افقی مشخص کردیم. سطح زیر نمودار قبل از چندک را با رنگ آبی مشخص نمودیم. مساحت قسمت آبی رنگ دقیقا برابر با 0.95 است.

مثال دو)

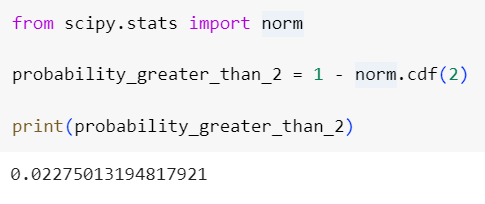
احتمال اینکه یک متغیر تصادفی ، (یعنی دو برابر انحراف معیار) بالاتر از میانگین باشد چقدر است؟

می‌توانیم بنویسیم:

با ساده‌سازی داریم:

در قطعه کد زیر به کمک کلاس توزیع نرمال در ماژول stats که در کتابخانه‌ی scipy پایتون پیاده‌سازی شده است، احتمال بالا را محاسبه می‌کنیم:

چند نکته در مورد توزیع نرمال

• اگر 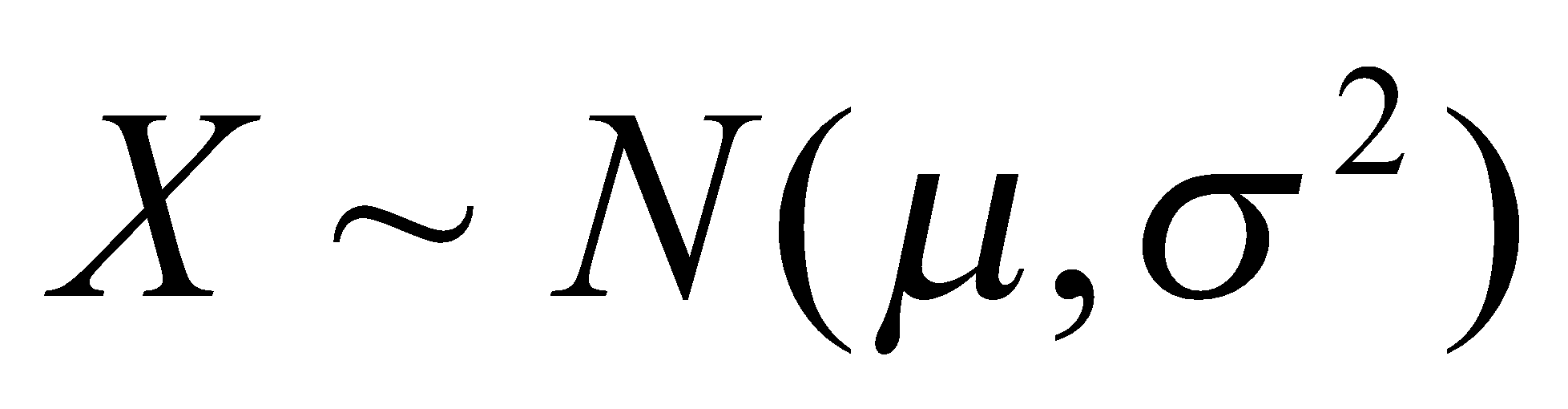، آنگاه  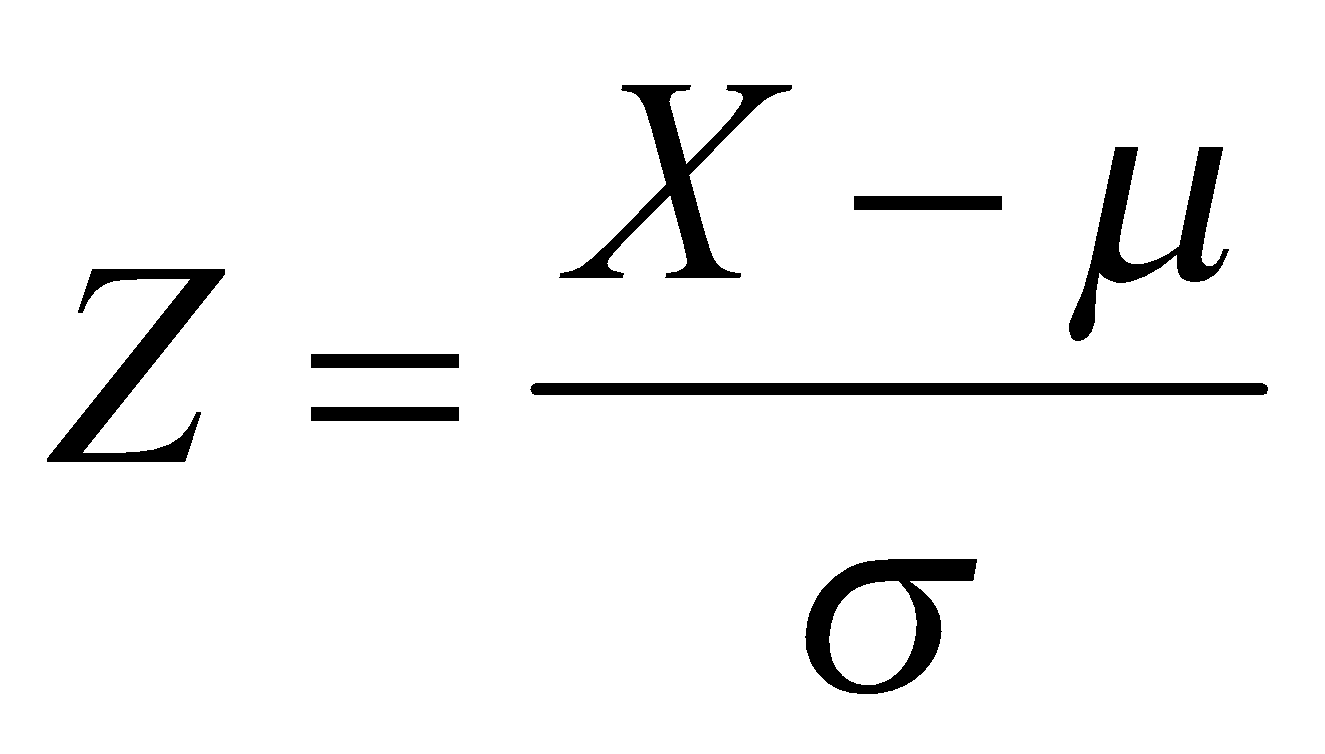دارای توزیع نرمال استاندارد خواهد بود.
• اگر 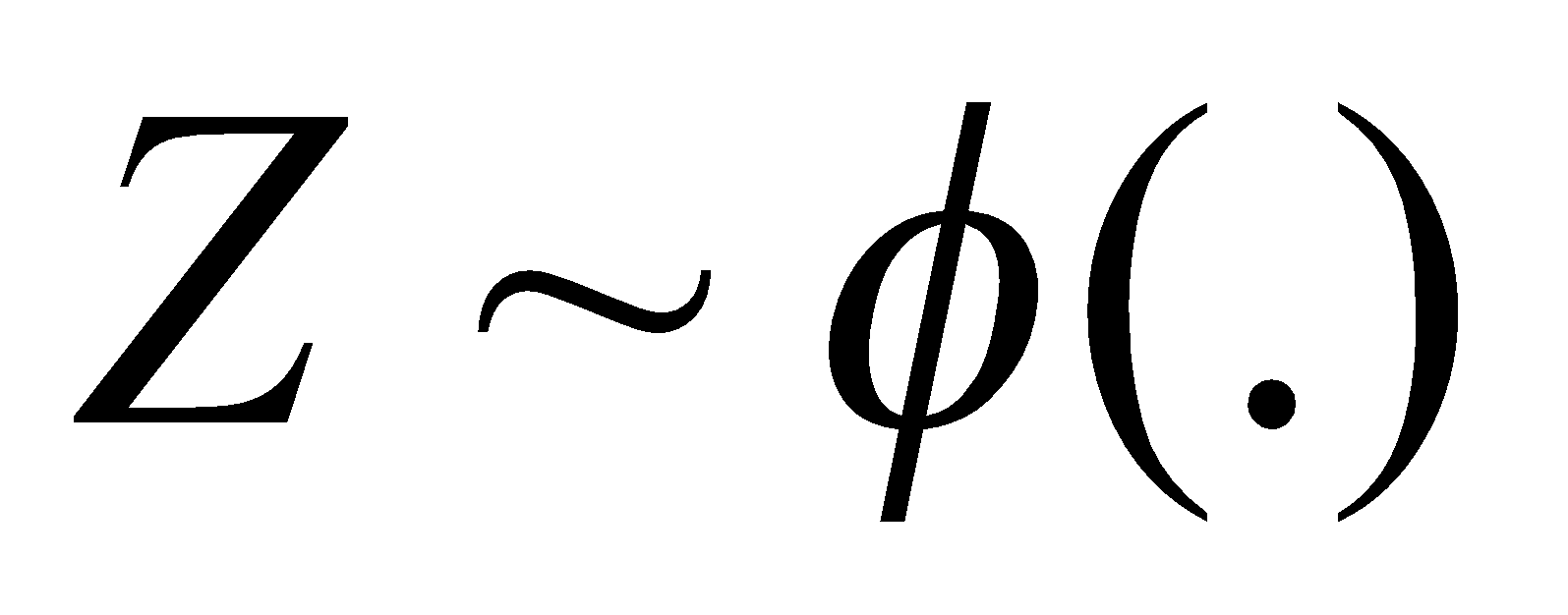، آنگاه .
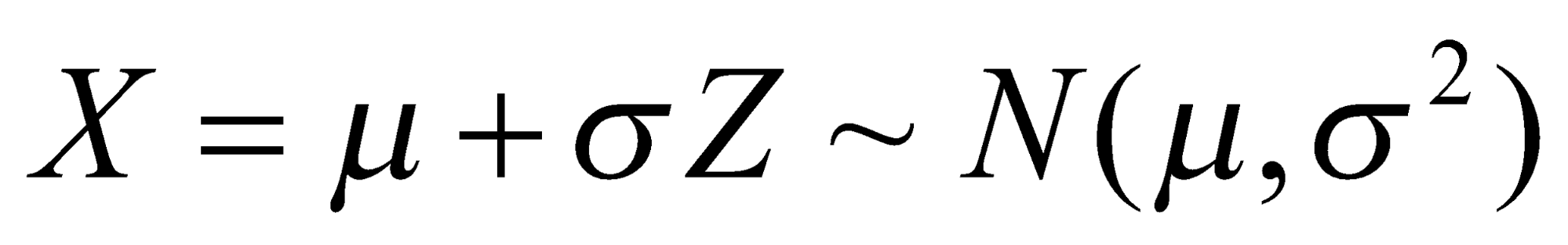• تابع چگالی احتمال هر توزیع نرمالی برحسب تابع چگالی احتمال نرمال استاندارد به صورت زیر قابل بازنویسی است:

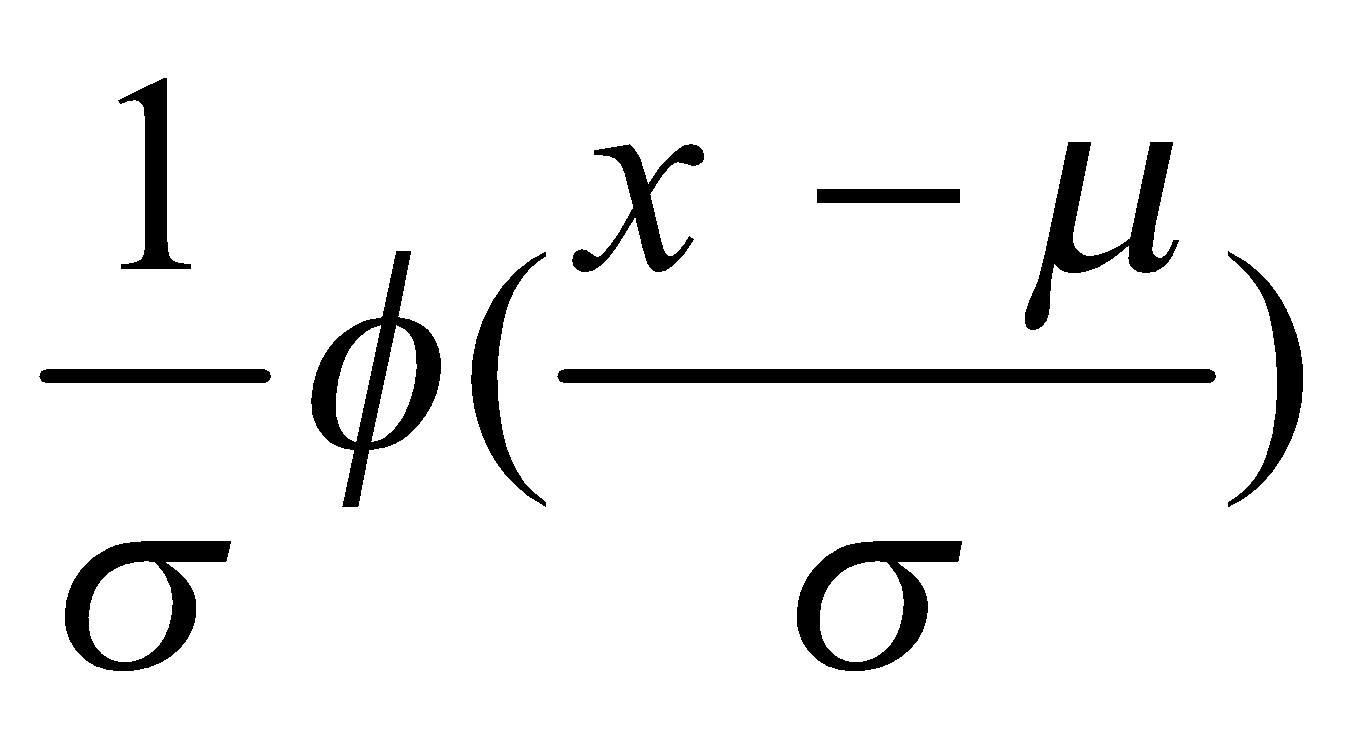
• به ترتیب تقریباً 68، 95، و 99.7 درصد چگالی احتمال توزیع نرمال در فاصله‌ی 1، 2، و 3 انحراف معیار از میانگین متمرکز است.
• به ترتیب 1.28-، 1.645-، 1.96-، . 2.33-، چندک‌های دهم، پنجم، دو و نیم، و اول توزیع نرمال استاندارد هستند.
• از آنجا که توزیع نرمال متقارن است، به ترتیب 1.28، 1.645، 1.96 و 2.33، چندک‌های نود، نود و پنج، نود و هفت و نیم، و نود و نهم توزیع نرمال استاندارد هستند.

خواص دیگر توزیع نرمال

• توزیع نرمال متقارن است و در حول میانگین خود متمرکز است (بنابراین میانگین، میانه و مد توزیع، همگی با هم برابر هستند).
• حاصل‌ضرب یک عدد ثابت در یک متغیر تصادفی با توزیع نرمال نیز توزیع نرمال دارد.
• مجموع متغیرهای تصادفی با توزیع نرمال، توزیع نرمال دارد حتی اگر متغیرها به یکدیگر وابسته باشند.
• میانگین نمونه‌ای متغیرهای تصادفی با توزیع نرمال، توزیع نرمال دارد. منظور از میانگین نمونه‌ای، میانگین نمونه‌های مشاهده‌شده است.
• مجذور یک متغیر تصادفی نرمال استاندارد از توزیع کای‌دو پیروی می‌کند.
• متغیر تصادفی با توزیع نرمال، با به توان رسیدن، از توزیع لُگ‌نرمال پیروی می‌کنند.

همان‌طور که در ادامه خواهیم دید، بسیاری از متغیرهای تصادفی که به درستی استاندارد شده‌اند، از توزیع نرمال پیروی می‌کنند.

3. منبع

https://aman.ai/primers/math/#correlation