آشنایی با حساب و دیفرانسیل
مقدمات حساب دیفترانسیل برای هوش مصنوعی: بدون دانستن این مطلب در هوش مصنوعی، کمیتتان لنگ است

چکیده
در این مقاله قصد داریم تا به بررسی حساب دیفرانسیل مورد نیاز در مباحث یادگیری ماشین بپردازیم. از سادهترین مفاهیم یعنی شیب یک راست شروع میکنیم، سپس به تعریف مشتق برای توابع یک و چند متغیره میپردازیم. در ادامه مفهوم مشتقات جزیی را معرفی میکنیم و قواعد محاسبهی مشتق را بیان میکنیم. همچنین به بررسی ارتباط مشتقگیری و بهینهسازی یک تابع میپردازیم و در این راستا الگوریتم گرادیان کاهشی را معرفی میکنیم. تلاش شده است تا از مثالهای عددی نیز در کنار مطالب تئوری استفاده شود تا درک مطلب آسانتر شود.
حساب دیفرانسیل
حساب دیفرانسیل و انتگرال یعنی مطالعه تغییرات پیوسته و دارای دو زیرشاخهی اصلی است: حساب دیفرانسیل که نرخ تغییر توابع را مطالعه و حساب انتگرال که سطح زیر منحنی را مطالعه میکند. در این یادداشت به بحث دربارهی اولی میپردازیم.
حساب دیفرانسیل هستهی اصلی یادگیری عمیق است؛ بنابراین مهم است که بدانیم مشتق و گرادیان یعنی چه و چگونه در یادگیری عمیق از آنها استفاده میشود و محدودیتهای آنها چیست.
شیب یک خط راست
شیب یک خط راست (غیر عمودی) را میتوان با گرفتن هر دو نقطهی دلخواه ![]() و
و ![]() روی خط و محاسبهی "افزایش دامنه" حساب کرد:
روی خط و محاسبهی "افزایش دامنه" حساب کرد:
![]()
در مثال زیر، ارتفاع (height) 3 و عرض (width) 6 است، بنابراین شیب برابر با ![]() است.
است.
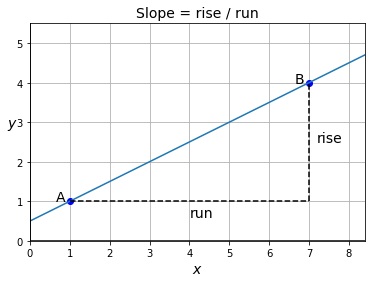
شکل 7: شیب یک خط راست
تعریف شیب یک منحنی
حال بیایید سعی کنیم که بفهمیم چگونه میتوانیم شیب یک تابع غیر از یک خط راست را محاسبه کنیم. برای مثال، منحنی تعریف شده توسط ![]() را در نظر میگیریم:
را در نظر میگیریم:
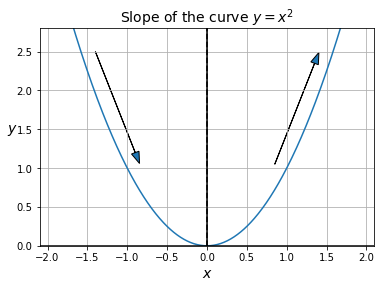
شکل 8: نمودار تابع ![]()
واضح است که شیب منحنی در قسمتهای مختلف، متفاوت است: در سمت چپ (یعنی وقتی ![]() )، شیب منفی است (یعنی وقتی از چپ به راست حرکت می کنیم، منحنی پایین می آید)، در حالی که در سمت راست (یعنی زمانی که
)، شیب منفی است (یعنی وقتی از چپ به راست حرکت می کنیم، منحنی پایین می آید)، در حالی که در سمت راست (یعنی زمانی که  ) شیب مثبت است (یعنی وقتی از چپ به راست حرکت می کنیم، منحنی بالا می رود). در نقطه
) شیب مثبت است (یعنی وقتی از چپ به راست حرکت می کنیم، منحنی بالا می رود). در نقطه ![]() ، شیب برابر با 0 است (یعنی منحنی در این ناحیه صاف است). این واقعیت که وقتی به حداقل (یا در واقع حداکثر) تابع می رسیم، شیب 0 است، بسیار مهم است و بعداً به آن باز خواهیم گشت.
، شیب برابر با 0 است (یعنی منحنی در این ناحیه صاف است). این واقعیت که وقتی به حداقل (یا در واقع حداکثر) تابع می رسیم، شیب 0 است، بسیار مهم است و بعداً به آن باز خواهیم گشت.
حال این سوال پیش میآید که چگونه می توانیم این شهودها را کمّی کنیم؟ فرض کنید میخواهیم شیب منحنی را در نقطهی دلخواه ![]() تخمین بزنیم؛ میتوانیم یک نقطهی دلخواه
تخمین بزنیم؛ میتوانیم یک نقطهی دلخواه ![]() روی منحنی را که از نقطهی
روی منحنی را که از نقطهی ![]() خیلی دور نباشد در نظر بگیریم و سپس شیب بین این دو نقطه را محاسبه کنیم.
خیلی دور نباشد در نظر بگیریم و سپس شیب بین این دو نقطه را محاسبه کنیم.
همانطور که میتوانید تصور کنید، وقتی نقطه![]() خیلی نزدیک به نقطه
خیلی نزدیک به نقطه ![]() است، خط
است، خط ![]() تقریباً از خود منحنی غیرقابل تشخیص میشود (حداقل به صورت محلی در اطراف نقطه
تقریباً از خود منحنی غیرقابل تشخیص میشود (حداقل به صورت محلی در اطراف نقطه ![]() ). خط
). خط ![]() به خط مماس بر منحنی در نقطه
به خط مماس بر منحنی در نقطه ![]() نزدیک و نزدیکتر میشود: این بهترین تقریب خطی منحنی در نقطهی
نزدیک و نزدیکتر میشود: این بهترین تقریب خطی منحنی در نقطهی ![]() است.
است.
بنابراین منطقی است که شیب منحنی در نقطه ![]() را به عنوان شیبی که خط
را به عنوان شیبی که خط ![]() (زمانی که
(زمانی که ![]() بینهایت به
بینهایت به ![]() نزدیک میشود) به آن میل میکند، تعریف کنیم. این شیب، مشتق تابع
نزدیک میشود) به آن میل میکند، تعریف کنیم. این شیب، مشتق تابع![]() در
در ![]() نامیده میشود. به عنوان مثال، مشتق تابع
نامیده میشود. به عنوان مثال، مشتق تابع ![]() در
در ![]() برابر با
برابر با ![]() است (به زودی نحوه بدست آوردن این نتیجه را خواهیم دید)، بنابراین در نمودار بالا، از آنجایی که نقطه
است (به زودی نحوه بدست آوردن این نتیجه را خواهیم دید)، بنابراین در نمودار بالا، از آنجایی که نقطه ![]() در
در ![]() قرار دارد، خط مماس بر منحنی در آن نقطه شیب
قرار دارد، خط مماس بر منحنی در آن نقطه شیب ![]() دارد.
دارد.
مشتقپذیری
توجه داشته باشید که همهی توابع به اندازهی ![]() خوشرفتار نیستند: برای مثال، تابع
خوشرفتار نیستند: برای مثال، تابع ![]() ، یعنی قدر مطلق
، یعنی قدر مطلق ![]() را در نظر بگیرید:
را در نظر بگیرید:
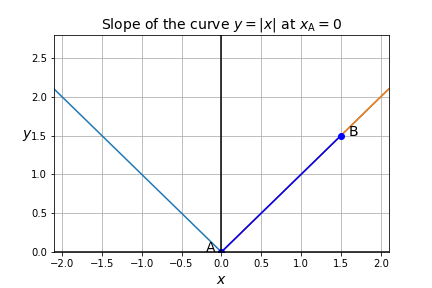
شکل 9: نمودار منحنی تابع قدر مطلق
مهم نیست که چقدر روی مبدا زوم کنید (نقطه ![]() )، منحنی همیشه شبیه یک
)، منحنی همیشه شبیه یک![]() خواهد بود. شیب برای هر
خواهد بود. شیب برای هر ![]() ،
، ![]() و برای هر یک
و برای هر یک ![]() ،
، ![]() است؛ اما در
است؛ اما در ![]() ، شیب تعریف نشده، زیرا امکان تقریب منحنی
، شیب تعریف نشده، زیرا امکان تقریب منحنی ![]() به صورت محلی در اطراف مبدا با استفاده از یک خط مستقیم میسر نیست.
به صورت محلی در اطراف مبدا با استفاده از یک خط مستقیم میسر نیست.
تابع ![]() در
در ![]() مشتقناپذیر است: یعنی مشتق آن در نقطهی
مشتقناپذیر است: یعنی مشتق آن در نقطهی ![]() تعریف نشده است. یعنی منحنی
تعریف نشده است. یعنی منحنی ![]() در آن نقطه شیب نامعینی دارد. اما تابع
در آن نقطه شیب نامعینی دارد. اما تابع ![]() در تمام نقاط دیگر مشتقپذیر است.
در تمام نقاط دیگر مشتقپذیر است.
برای اینکه تابع ![]() در نقطهی
در نقطهی ![]() مشتقپذیر باشد، باید وقتی که
مشتقپذیر باشد، باید وقتی که ![]() بینهایت به
بینهایت به ![]() نزدیک میشود، شیب خط
نزدیک میشود، شیب خط ![]() به یک مقدار معین میل می کند.
به یک مقدار معین میل می کند.
این موضوع مستلزم چند شرط است:
ابتدا، تابع البته باید در ![]() تعریفشده باشد. به عنوان مثال، تابع
تعریفشده باشد. به عنوان مثال، تابع ![]() در
در ![]() تعریف نشده است، بنابراین در این نقطه مشتقپذیر نیست.
تعریف نشده است، بنابراین در این نقطه مشتقپذیر نیست.
تابع همچنین باید در ![]() پیوسته باشد، به این معنی که وقتی
پیوسته باشد، به این معنی که وقتی ![]() بینهایت به
بینهایت به ![]() نزدیک میشود،
نزدیک میشود، ![]() نیز باید بی نهایت به
نیز باید بی نهایت به ![]() نزدیک شود.
نزدیک شود.
به عنوان مثال،
![]()
اگرچه در ![]() تعریفشده است، پیوسته نیست: در واقع، وقتی از سمت منفی به آن نقطه نزدیک میشوید، مقدار تابع در بینهایت به
تعریفشده است، پیوسته نیست: در واقع، وقتی از سمت منفی به آن نقطه نزدیک میشوید، مقدار تابع در بینهایت به ![]() نزدیک نمیشود. بنابراین، در آن نقطه پیوسته نیست و مشتقپذیر نیز نیست.
نزدیک نمیشود. بنابراین، در آن نقطه پیوسته نیست و مشتقپذیر نیز نیست.
تابع نباید درنقطهی ![]() شکستگی داشته باشد، به این معنی که شیبهایی که خط
شکستگی داشته باشد، به این معنی که شیبهایی که خط ![]() با نزدیک شدن دوطرفهی
با نزدیک شدن دوطرفهی ![]() به
به ![]() به آن میل میکند، باید یکسان باشند. قبلاً یک مثال نقص با
به آن میل میکند، باید یکسان باشند. قبلاً یک مثال نقص با ![]() دیدیم که در نقطهی
دیدیم که در نقطهی ![]() هم تعریف شده و هم پیوسته است، اما در
هم تعریف شده و هم پیوسته است، اما در ![]() شکستگی وجود دارد: شیب منحنی
شکستگی وجود دارد: شیب منحنی ![]() در سمت چپ
در سمت چپ ![]() و در سمت راست
و در سمت راست ![]() است.
است.
منحنی ![]() نباید در نقطه
نباید در نقطه ![]() عمودی باشد. یک مثال برای این موضوع
عمودی باشد. یک مثال برای این موضوع ![]() است: منحنی این تابع در مبدأ مختصات عمودی است بنابراین تابع در
است: منحنی این تابع در مبدأ مختصات عمودی است بنابراین تابع در ![]() مشتقپذیر نیست.
مشتقپذیر نیست.
مشتقگیری از یک تابع
حالا بیایید ببینیم که چگونه میتوانیم مشتق یک تابع را پیدا کنیم.
مشتق تابع ![]() در
در ![]() با
با ![]() مشخص میشود و به صورت زیر تعریف میشود:
مشخص میشود و به صورت زیر تعریف میشود:
![]()
نترسید، این ساده تر از چیزی است که به نظر می رسد! ممکن است افزایش معادله 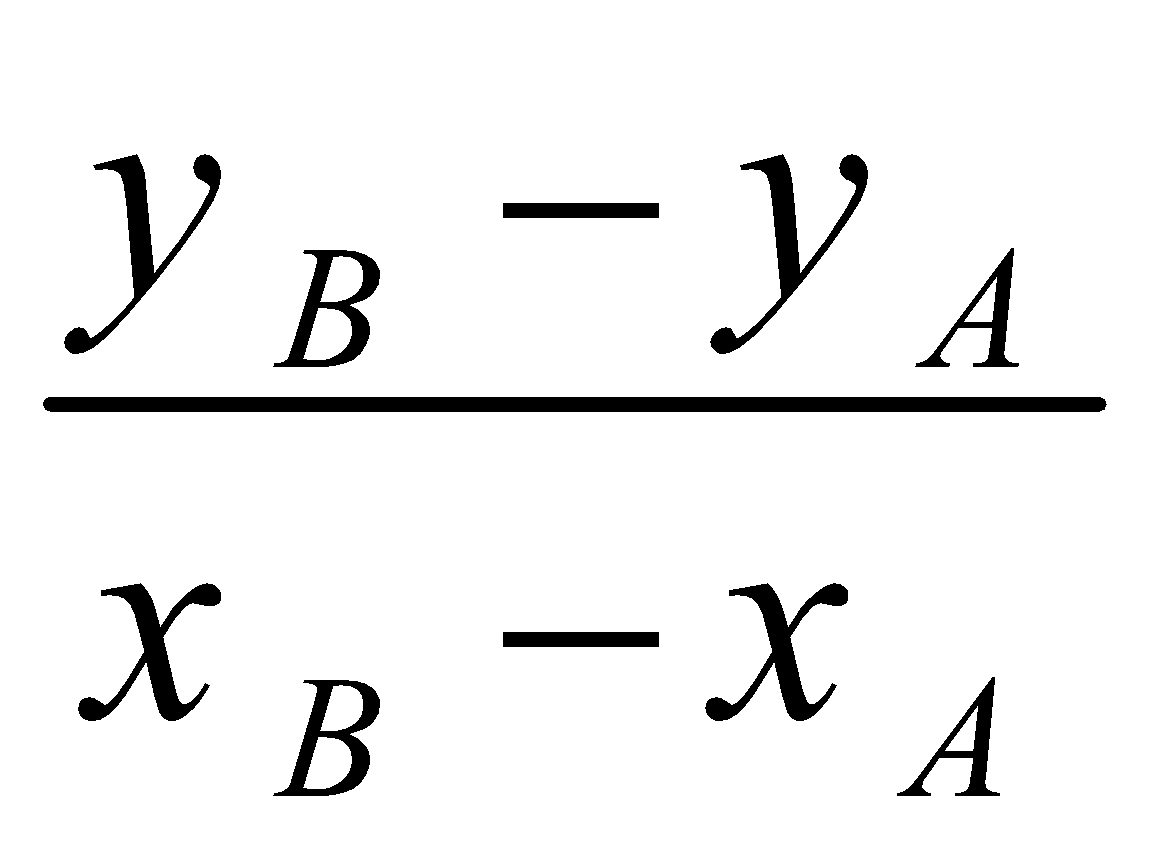 را که قبلاً در مورد آن صحبت کردیم، به یاد بیاورید. رابطهی بالا همان شیب خط
را که قبلاً در مورد آن صحبت کردیم، به یاد بیاورید. رابطهی بالا همان شیب خط ![]() است. و نماد
است. و نماد 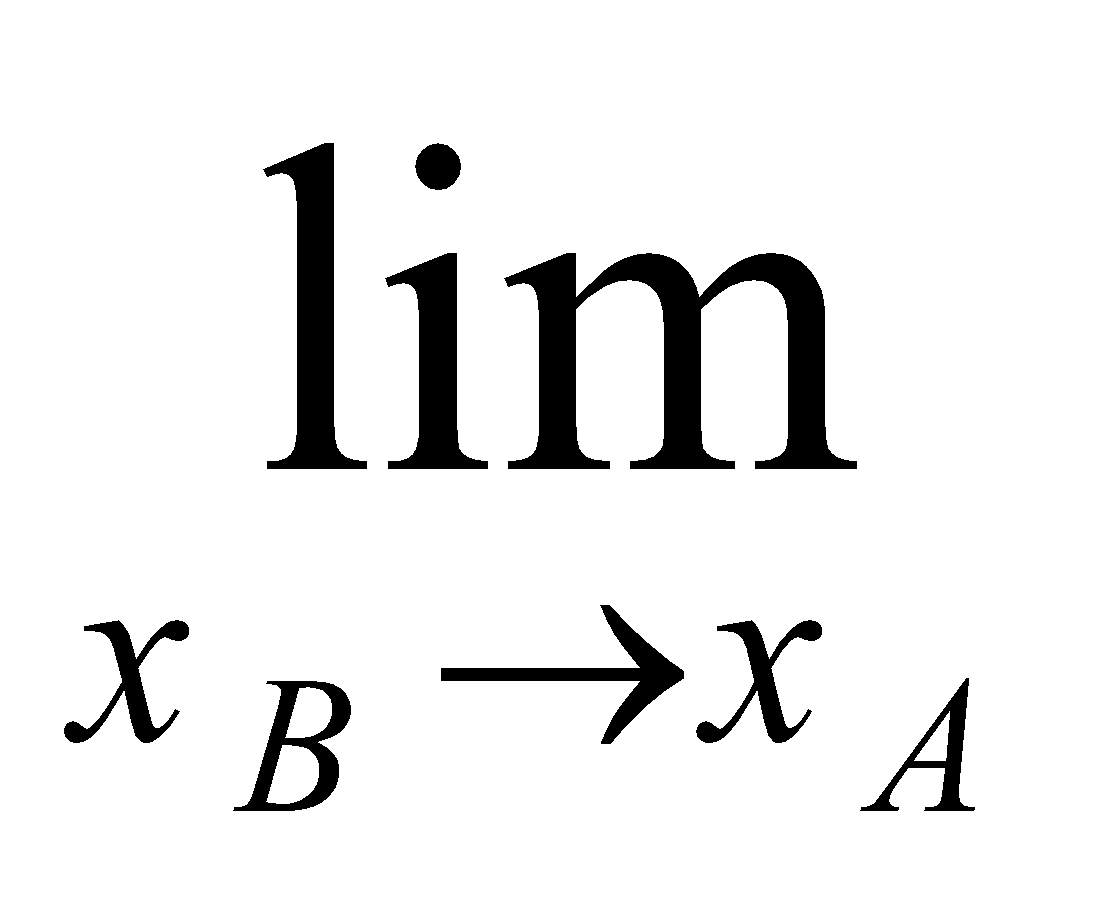 به این معنی است که ما
به این معنی است که ما ![]() را بی نهایت به
را بی نهایت به ![]() نزدیک میکنیم. بنابراین به زبان ساده،
نزدیک میکنیم. بنابراین به زبان ساده، ![]() مقداری است که شیب خط
مقداری است که شیب خط ![]() هنگامی که
هنگامی که ![]() بینهایت به
بینهایت به ![]() نزدیک می شود، اختیار میکند. این تنها یک روش رسمی برای گفتن دقیقا همان چیزی است که قبلاً گفته شد.
نزدیک می شود، اختیار میکند. این تنها یک روش رسمی برای گفتن دقیقا همان چیزی است که قبلاً گفته شد.
مثال: یافتن مشتق تابع ![]()
بیایید ببینیم آیا میتوانیم شیب منحنی ![]() را در نقطهی دلخواه
را در نقطهی دلخواه ![]() تعیین کنیم:
تعیین کنیم:
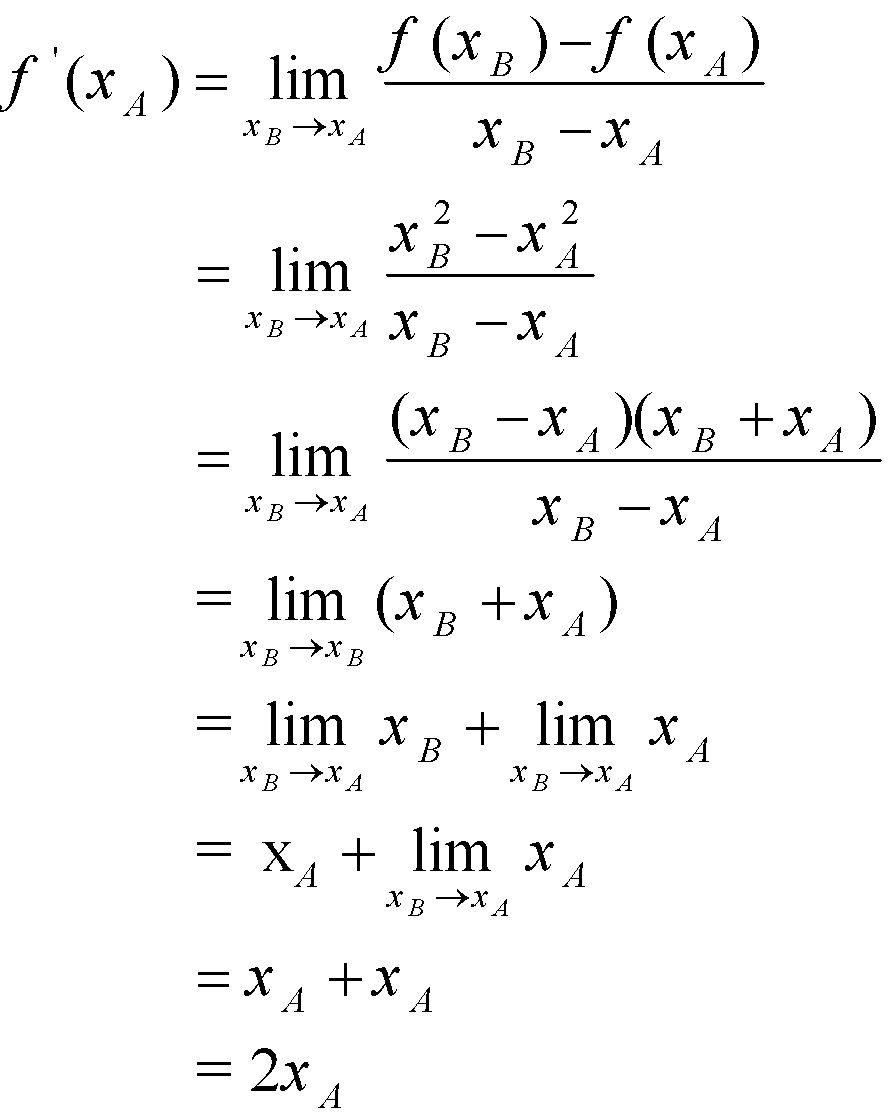
به همین سادگی! ما ثابت کردیم که شیب ![]() در هر نقطهی دلخواه
در هر نقطهی دلخواه![]() برابر با
برابر با ![]() است. کاری که انجام دادیم مشتقگیری نامیده می شود یعنی یافتن مشتق یک تابع.
است. کاری که انجام دادیم مشتقگیری نامیده می شود یعنی یافتن مشتق یک تابع.
توجه داشته باشید که ما در اثبات بالا از چند ویژگی مهم حدها استفاده کردیم. در اینجا ویژگیهای اصلی حدگیری توابع که برای کار با مشتقات باید بدانید را مرور میکنیم:
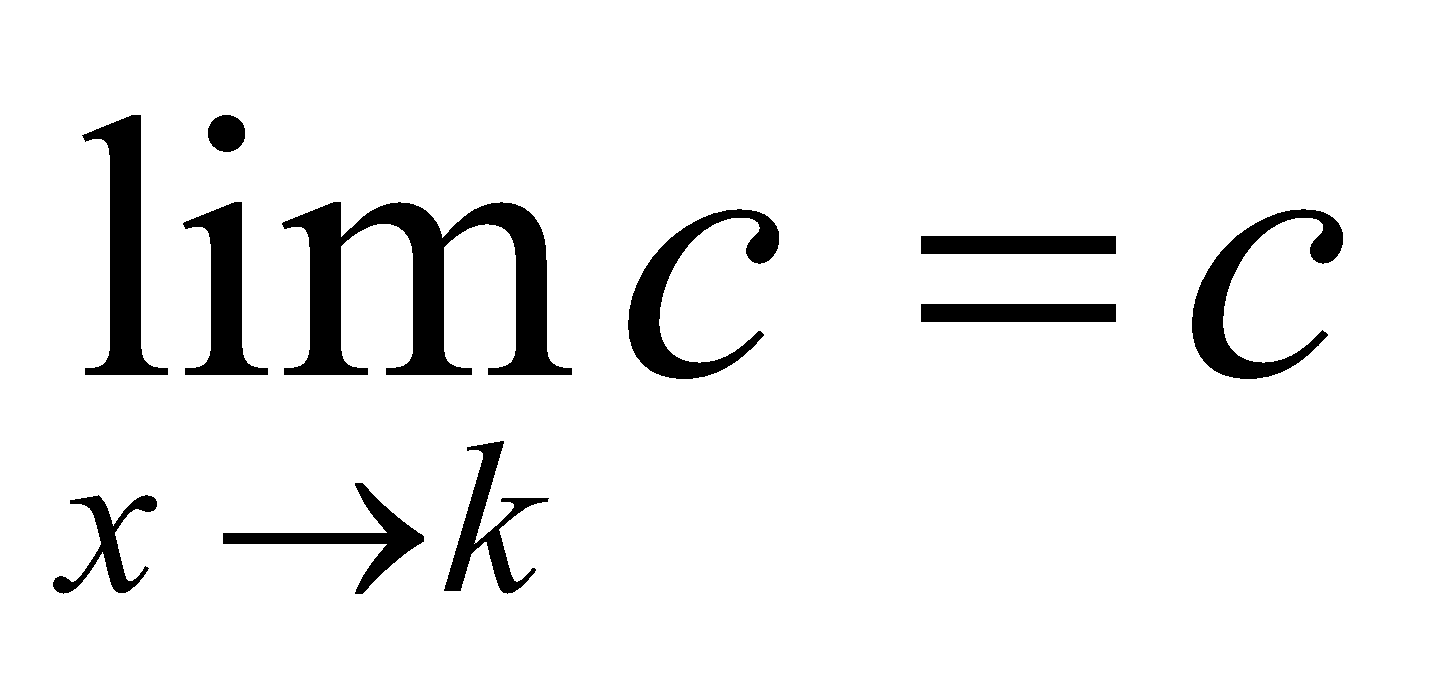 اگر
اگر  مقدار ثابتی باشد که به
مقدار ثابتی باشد که به 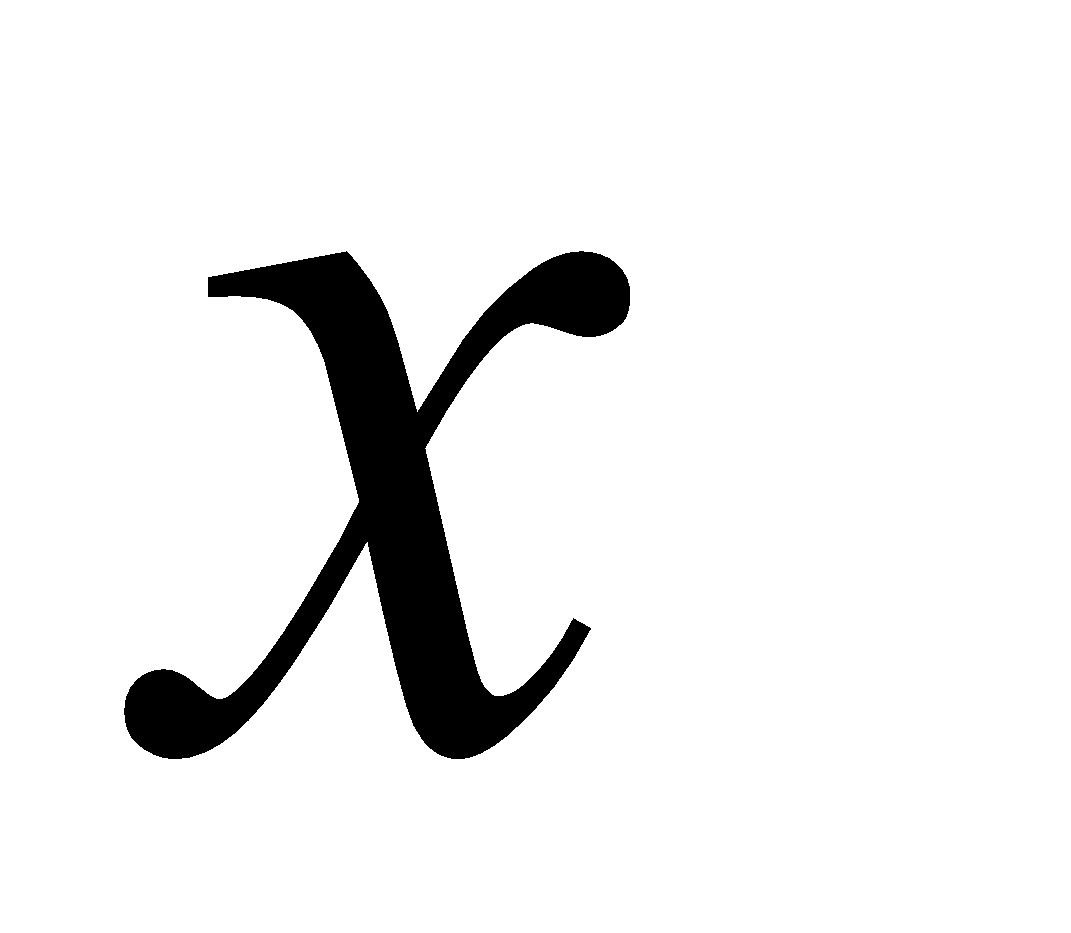 بستگی ندارد، آنگاه حد برابر
بستگی ندارد، آنگاه حد برابر است.
است.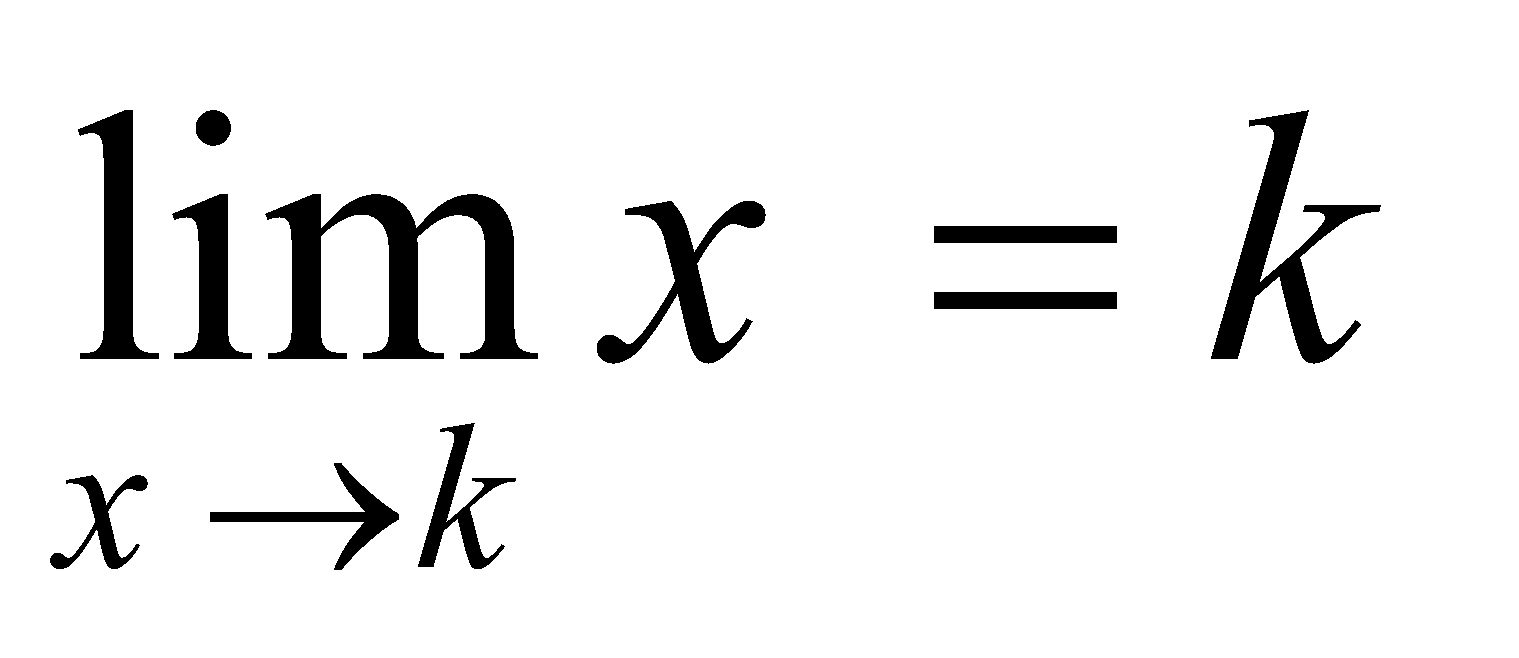 اگر
اگر 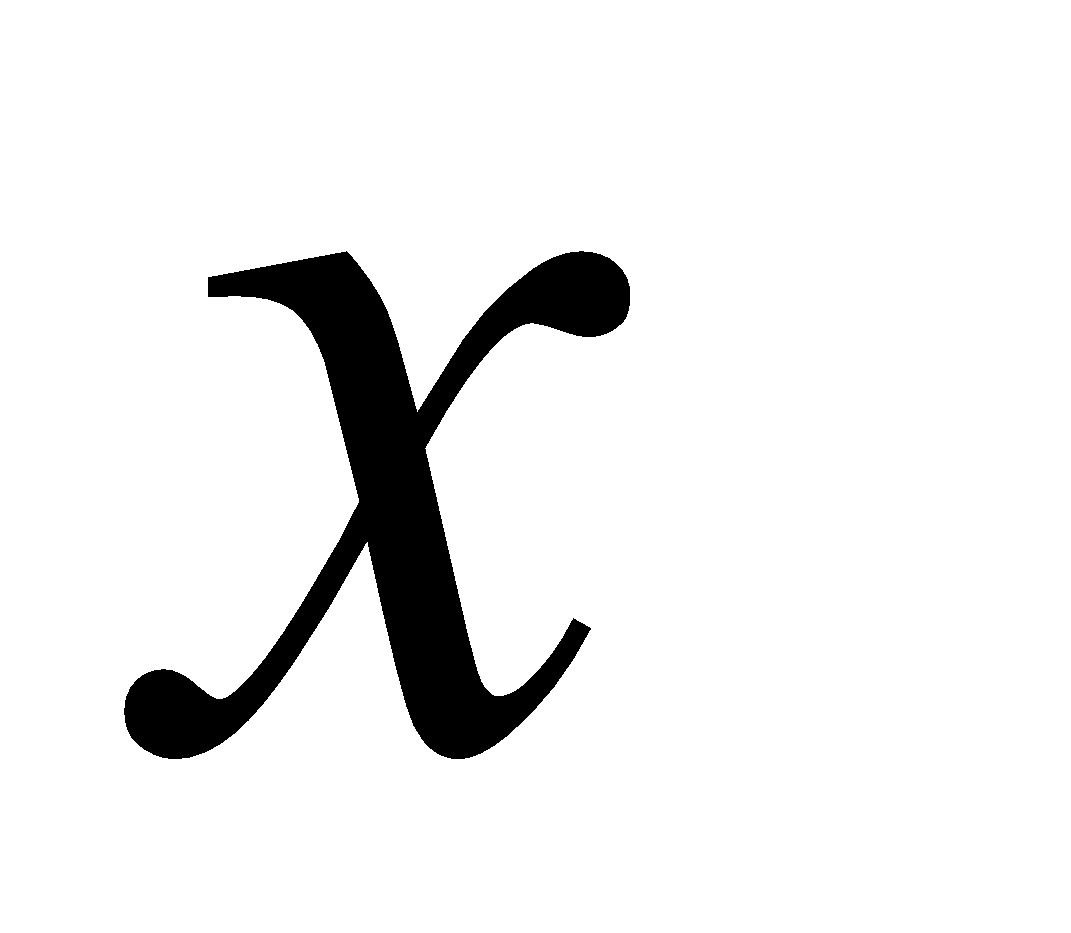 به مقدار
به مقدار 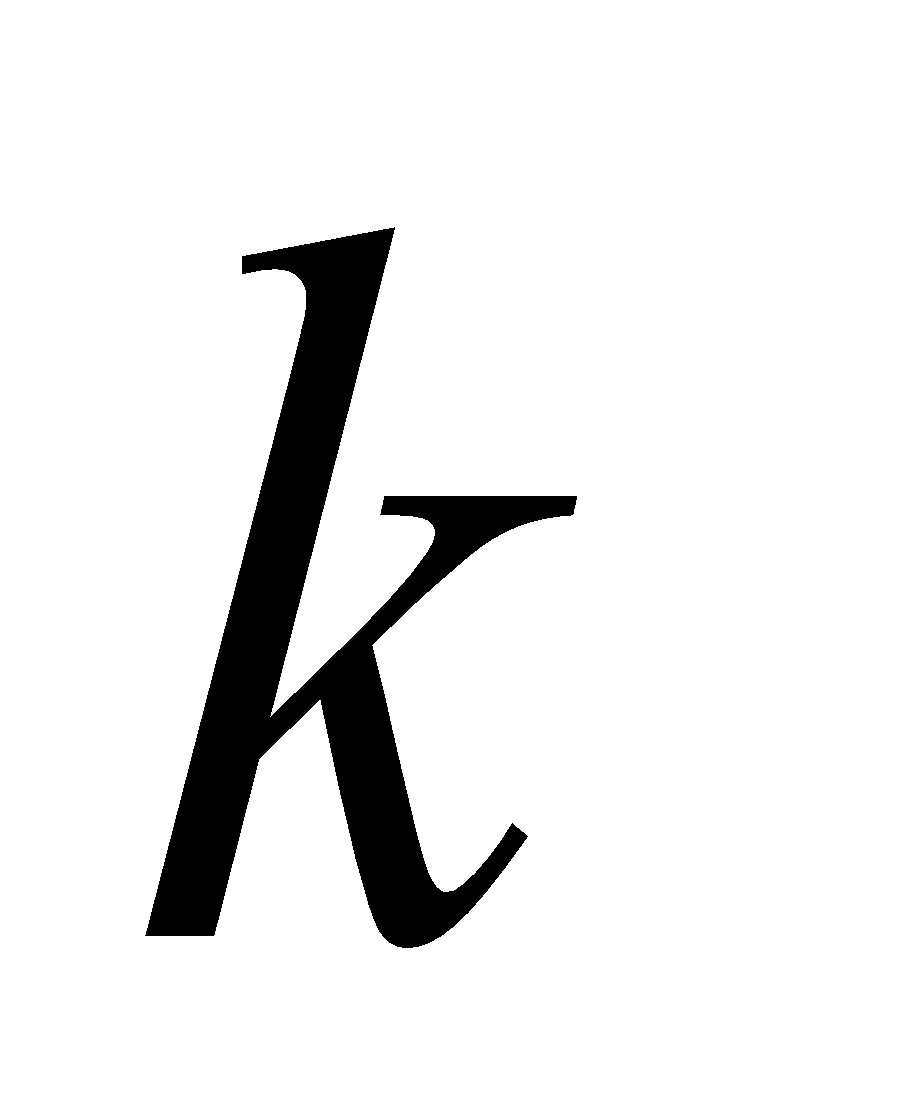 نزدیک شود، حد آن
نزدیک شود، حد آن 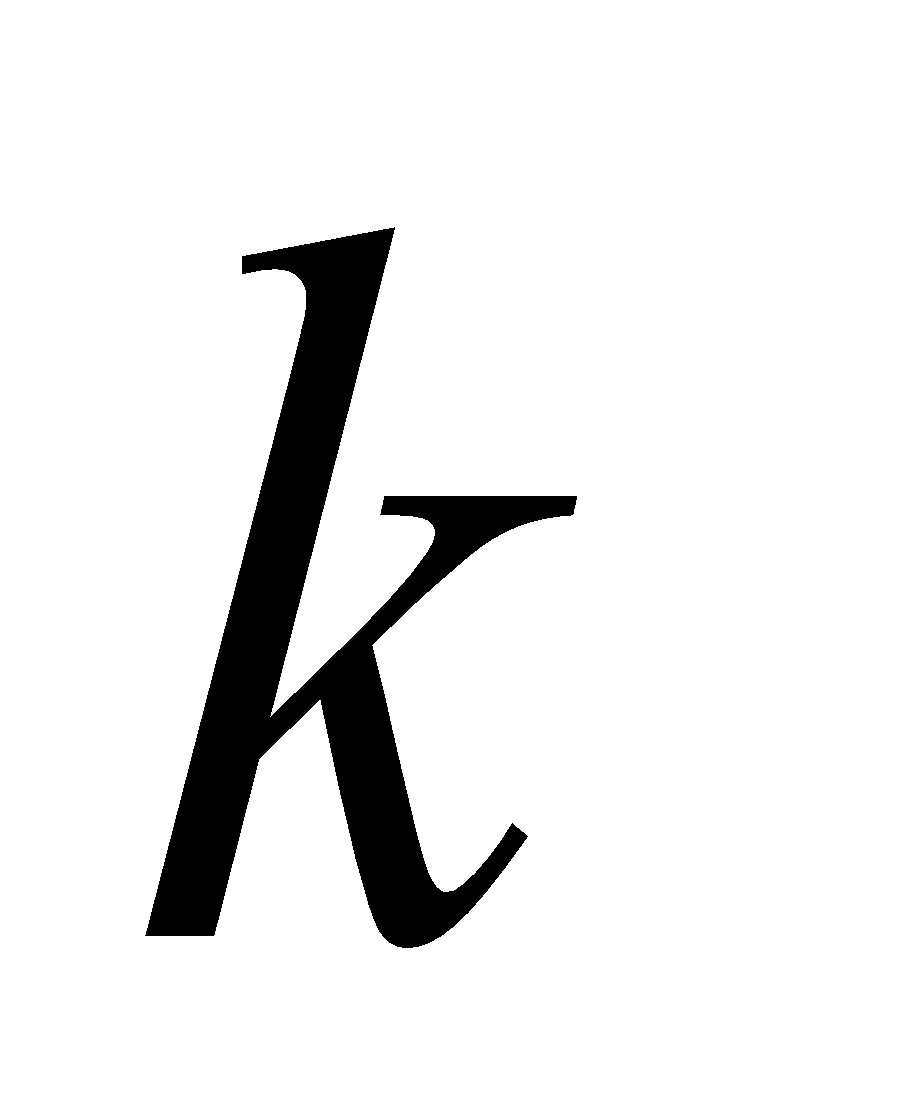 است.
است.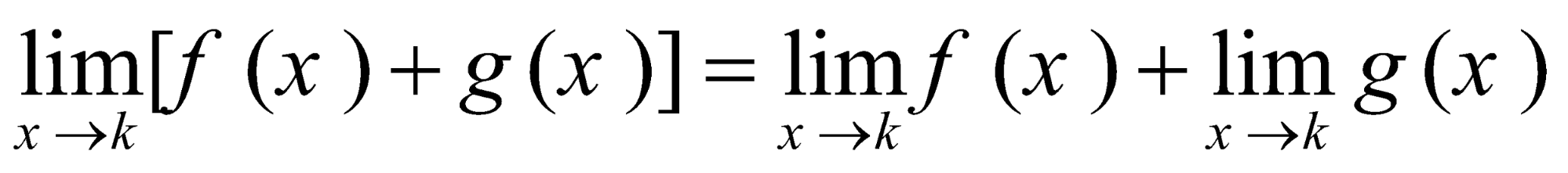 حد یک عبارت جمع، مجموع حدود است.
حد یک عبارت جمع، مجموع حدود است.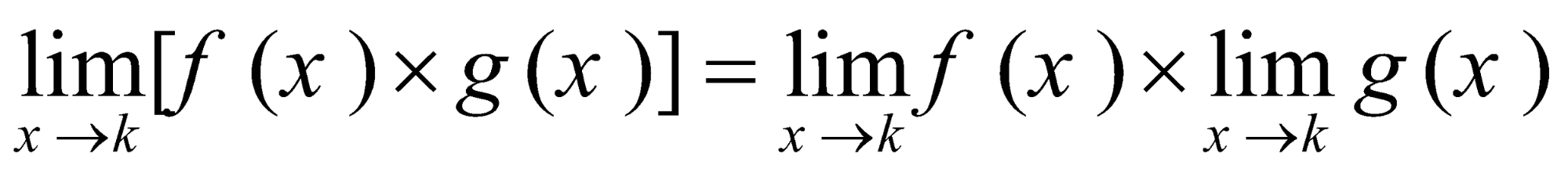 حد یک عبارت ضرب، حاصل ضرب حدهاست.
حد یک عبارت ضرب، حاصل ضرب حدهاست.
نکته مهم: دریادگیری عمیق، مشتقگیری تقریباً همیشه به طور خودکار توسط کتابخانهای که استفاده میکنید (مانند TensorFlow یا PyTorch) انجام میشود. به این حالت مشتقگیری خودکار میگویند. با این حال، همچنان باید مطمئن شوید که درک خوبی از فرایند مشتقگیری دارید، وگرنه آنها ممکن است یک روز برای شما ایجاد مشکل کند. به عنوان مثال ممکن است از یک عبارت جذر در تابع هزینهی مدل خود استفاده میکنید بدون اینکه متوجه باشید که مشتق آن وقتی که ![]() به 0 میل میکند، به بینهایت نزدیک میشود (راهنمایی: باید از
به 0 میل میکند، به بینهایت نزدیک میشود (راهنمایی: باید از ![]() استفاده کنید که در آن
استفاده کنید که در آن ![]() یک مقدار بسیار کوچک است مانند
یک مقدار بسیار کوچک است مانند ![]() ).
).
شما اغلب یک تعریف کمی متفاوت (اما معادل) از مشتق را در منابع دیگر پیدا خواهید کرد. بیایید آن را از تعریف قبلی که ارائه دادیم استخراج کنیم. ابتدا بیایید ![]() را تعریف کنیم. توجه داشته باشید که
را تعریف کنیم. توجه داشته باشید که ![]() با نزدیک شدن
با نزدیک شدن ![]() به
به ![]() ، به 0 نزدیک میشود. در آخر توجه داشته باشید که
، به 0 نزدیک میشود. در آخر توجه داشته باشید که ![]() . با این رابطه، میتوانیم تعریف فوق را به این صورت دوباره فرمولبندی کنیم:
. با این رابطه، میتوانیم تعریف فوق را به این صورت دوباره فرمولبندی کنیم:
![]()
بیایید فقط ![]() را به
را به ![]() تغییر نام دهیم تا مجبور نباشیم اندیس
تغییر نام دهیم تا مجبور نباشیم اندیس ![]() را هربار تکرار کنیم و خواندن روابط راحتتر شود:
را هربار تکرار کنیم و خواندن روابط راحتتر شود:
![]()
حال بیایید از این تعریف جدید برای یافتن مشتق ![]() در نقطهی دلخواه
در نقطهی دلخواه![]() استفاده کنیم. باید به همان نتیجه بالا برسیم.
استفاده کنیم. باید به همان نتیجه بالا برسیم.
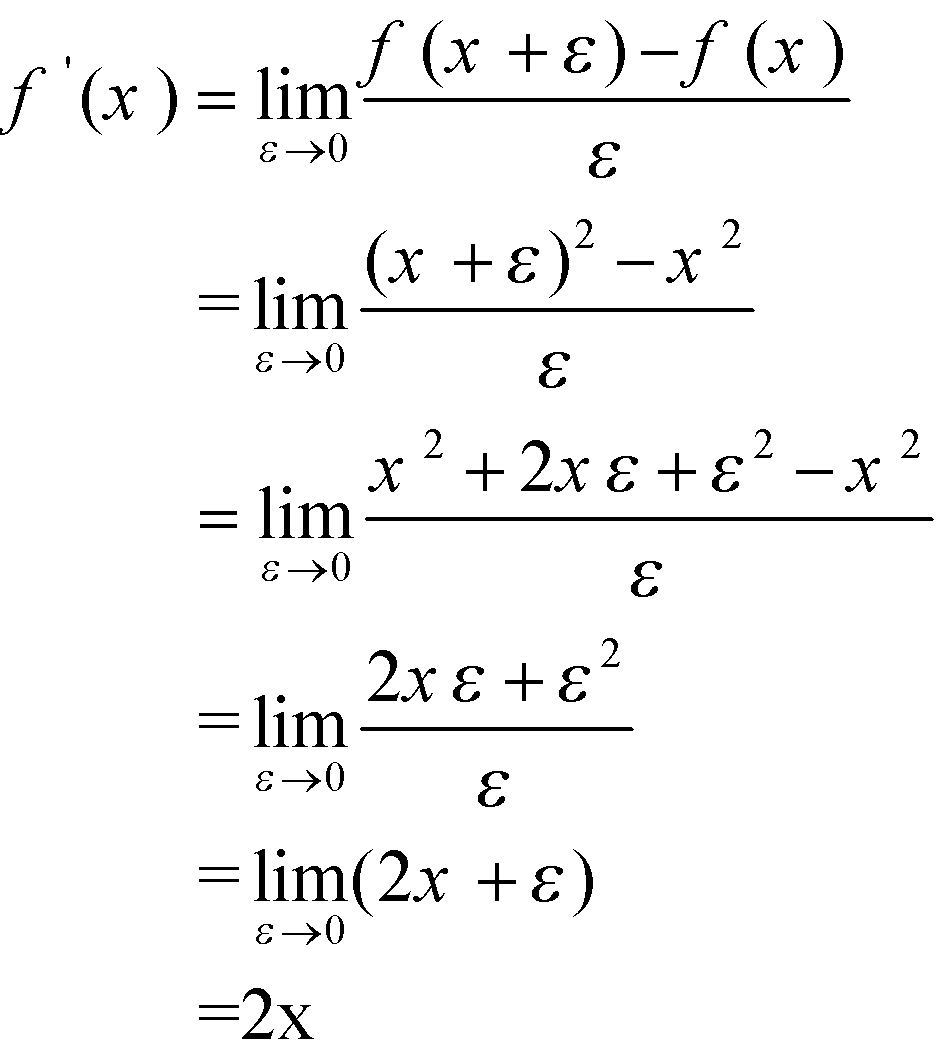
همانطور که مشاهده میکنید، این نتیجه با نتیجهای که قبلاً به دست آورده بودیم، مطابقت دارد.
نمادگذاری
چندین نماد مختلف برای نمایش مشتق توابع وجود دارد که در منابع مرتبط خواهید یافت.
![]()
این نماد همچنین زمانی مفید است که تابع به طور صریح نامگذاری نشده باشد. برای مثال ![]() به مشتق تابع
به مشتق تابع ![]() اشاره دارد.
اشاره دارد.
علاوه بر این، معمولا وقتی مردم در مورد تابع ![]() صحبت می کنند، گاهی اوقات
صحبت می کنند، گاهی اوقات ![]() را کنار می گذارند و فقط در مورد تابع
را کنار می گذارند و فقط در مورد تابع ![]() صحبت میکنند. در این موارد نماد مشتق نیز ساده تر است:
صحبت میکنند. در این موارد نماد مشتق نیز ساده تر است:
![]()
نماد ![]() نماد لاگرانژ است، در حالی که
نماد لاگرانژ است، در حالی که ![]() نماد لایبنیتس است.
نماد لایبنیتس است.
نمادهای کمتر رایج دیگری نیز وجود دارد، مانند نماد نیوتن ![]() با فرض
با فرض ![]() یا نماد اویلر:
یا نماد اویلر:![]() .
.
قواعد مشتقگیری
یک قانون بسیار مهم این است که مشتق یک عبارت مجموع، برابر با مجموع مشتقات اجزا است. به طور دقیق تر، اگر ![]() را تعریف کنیم، آنگاه
را تعریف کنیم، آنگاه ![]() . اثبات این موضوع بسیار آسان است:
. اثبات این موضوع بسیار آسان است:
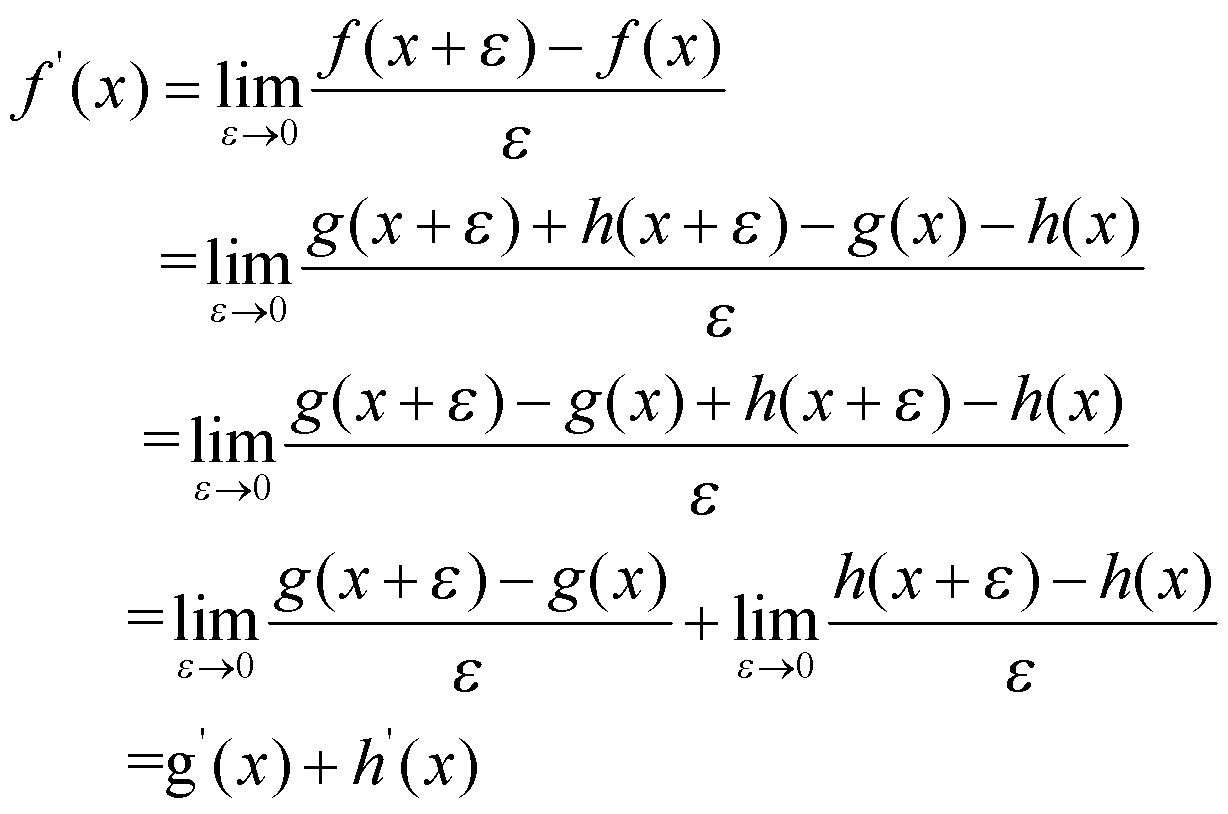
به طور مشابه، میتوان قوانین مهم زیر را نشان داد:
جدول 1: قواعد مهم مشتقگیری
مشتق( | تابع( | |
|
| ثابت |
|
| جمع |
|
| ضرب |
|
| تقسیم |
|
| توان |
|
| نمایی |
|
| لگاریتم |
|
| سینوس |
|
| کسینوس |
|
| تانژانت |
|
| قاعدهی زنجیرهای |
بیایید سعی کنیم تا از یک تابع ساده، با استفاده از قوانین بالا مشتق بگیریم: تابع ![]() را در نظر میگیریم. با استفاده از قانون مشتق مجموع متوجه میشویم که
را در نظر میگیریم. با استفاده از قانون مشتق مجموع متوجه میشویم که ![]() .با استفاده از قاعده مشتقگیری از عبارات توانی و تابع کسینوسی، متوجه میشویم که
.با استفاده از قاعده مشتقگیری از عبارات توانی و تابع کسینوسی، متوجه میشویم که ![]() .
.
بیایید یک مثال سختتر را امتحان کنیم: تابع ![]() را در نظر بگیرید. ابتدا،
را در نظر بگیرید. ابتدا، ![]() و
و ![]() را تعریف میکنیم. با استفاده از قانون مشتقگیری عبارت مجموع، متوجه میشویم که
را تعریف میکنیم. با استفاده از قانون مشتقگیری عبارت مجموع، متوجه میشویم که ![]() .در نتیجه
.در نتیجه ![]() . سپس، با استفاده از قانون عبارت ضربی، متوجه میشویم که
. سپس، با استفاده از قانون عبارت ضربی، متوجه میشویم که ![]() .از آنجایی که مشتق تابع ثابت 0 است، جمله دوم 0 میشود. و از آنجایی که قانون توان به ما میگوید که مشتق
.از آنجایی که مشتق تابع ثابت 0 است، جمله دوم 0 میشود. و از آنجایی که قانون توان به ما میگوید که مشتق ![]() ،
، ![]() است، متوجه میشویم که
است، متوجه میشویم که ![]() است. در نهایت، با استفاده از قاعدهی زنجیرهای، از آنجایی که
است. در نهایت، با استفاده از قاعدهی زنجیرهای، از آنجایی که ![]() ، درمییابیم که
، درمییابیم که ![]() .
.
مشتقات و بهینه سازی تابع
هنگامی که سعی میکنیم تابع ![]() را بهینه کنیم، به دنبال مقادیری برای
را بهینه کنیم، به دنبال مقادیری برای ![]() میگردیم که تابع را کمینه (یا بیشینه) میکند.
میگردیم که تابع را کمینه (یا بیشینه) میکند.
توجه به این نکتهی مهمی است که وقتی یک تابع به حداقل یا حداکثر خود میرسد، با فرض اینکه در آن نقطه مشتقپذیر باشد، مشتق الزاماً برابر با 0 خواهد بود. به عنوان مثال، می توانید نمودار پایین را بررسی کنید و توجه کنید که هر زمان که تابع حداکثر یا حداقل مقدار خود را اختیار میکند، مشتق آن برابر با 0 است.
بنابراین یکی از راههای بهینهسازی یک تابع، مشتقگیری از آن و یافتن تحلیلی تمام مقادیری است که مشتق در آن نقاط برابر با 0 است. سپس تعیین میکنیم که کدام یک از این مقادیر، تابع را بهینه میکنند (در صورت وجود). برای مثال تابع ![]() را در نظر بگیرید. با استفاده از قوانین مشتق (به طور خاص، قانون جمع، قانون حاصلضرب، قانون توان و قانون تابع ثابت)، متوجه میشویم که
را در نظر بگیرید. با استفاده از قوانین مشتق (به طور خاص، قانون جمع، قانون حاصلضرب، قانون توان و قانون تابع ثابت)، متوجه میشویم که ![]() . ما به دنبال مقادیری برای
. ما به دنبال مقادیری برای ![]() میگردیم که در آنها
میگردیم که در آنها ![]() ، بنابراین باید معادلهی
، بنابراین باید معادلهی ![]() را حل کنیم. پس داریم
را حل کنیم. پس داریم ![]() بنابراین
بنابراین ![]() یا
یا ![]() یا
یا ![]() .همانطور که در نمودار زیر میبینید، این 3 مقدار، نقاط اکسترمم تابع در بازهی نمایش دادهشده هستند. دو حداقل کلی (در کل دامنه)
.همانطور که در نمودار زیر میبینید، این 3 مقدار، نقاط اکسترمم تابع در بازهی نمایش دادهشده هستند. دو حداقل کلی (در کل دامنه) ![]() و یک حداکثر محلی
و یک حداکثر محلی ![]() .
.
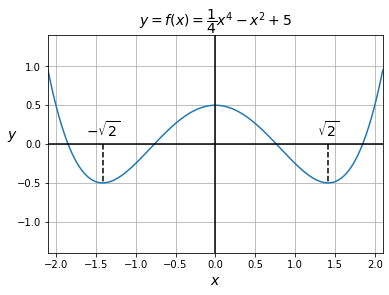
شکل 10: نمودار تابع ![]()
اگر تابعی در نقطهی ![]() یک اکسترمم محلی داشته باشد و در آن نقطه مشتقپذیر باشد،داریم
یک اکسترمم محلی داشته باشد و در آن نقطه مشتقپذیر باشد،داریم ![]() . با این حال، همیشه برعکس آن صادق نیست. برای مثال،
. با این حال، همیشه برعکس آن صادق نیست. برای مثال، ![]() را در نظر بگیرید. مشتق آن برابر
را در نظر بگیرید. مشتق آن برابر ![]() است که در
است که در ![]() ، مشتق برابر با 0 است. با این حال، همانطور که در نمودار زیر می بینید، این نقطه یک نقطهی اکسترمم نیست. این صرفا یک نقطه است که شیب آن برابر با 0 است.
، مشتق برابر با 0 است. با این حال، همانطور که در نمودار زیر می بینید، این نقطه یک نقطهی اکسترمم نیست. این صرفا یک نقطه است که شیب آن برابر با 0 است.
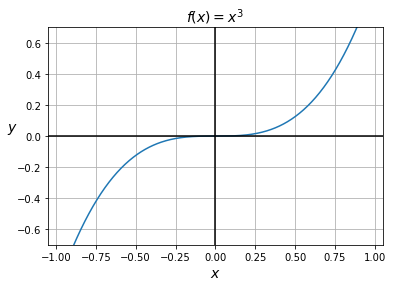
شکل 11: نمودار تابع ![]()
بنابراین به طور خلاصه، می توانید یک تابع را با بررسی تحلیلی نقاطی که مشتق در آنها 0 است، بهینه کنید و سپس فقط این نقاط را بررسی کنید. این راه حل زیبا و هوشمندانه است، اما به زحمت زیادی نیاز دارد و همیشه آسان و یا حتی ممکن نیست. برای شبکههای عصبی، عملا غیرممکن است.
یکی دیگر از گزینههای بهینهسازی یک تابع، اجرای الگوریتم گرادیان کاهشی است (ما کمینه کردن تابع را در نظر خواهیم گرفت، اما اگر بخواهیم یک تابع را حداکثر کنیم نیز فرآیند الگوریتم تقریباً یکسان خواهد بود): از نقطهی تصادفی ![]() شروع کنید، سپس از مشتق تابع در نقطهی
شروع کنید، سپس از مشتق تابع در نقطهی ![]() برای تعیین شیب استفاده کنید. سپس کمی در خلاف جهت شیب حرکت کنید. این روند را تکرار کنید تا به کمینهی محلی برسید، و امیدوار باشید که این نقطه، یک حداقل کلی روی تمام دامنهی تابع باشد.
برای تعیین شیب استفاده کنید. سپس کمی در خلاف جهت شیب حرکت کنید. این روند را تکرار کنید تا به کمینهی محلی برسید، و امیدوار باشید که این نقطه، یک حداقل کلی روی تمام دامنهی تابع باشد.
در هر بار تکرار فرایند، اندازهی گام حرکت متناسب با شیب در آن نقطه است، بنابراین حرکت به طور طبیعی با نزدیک شدن به نقطهی حداقل محلی کند میشود. هر گام همچنین متناسب با نرخ یادگیری نیز است که خود پارامتری از الگوریتم گرادیان کاهشی است. چون نرخ یادگیری پارامتر تابعی که آن را بهینه میکنیم نیست، به آن ابرپارامتر میگویند. در واقع مقدار ابرپارامترها بر روی خروجی الگوریتم تاثیر میگذارند و باید به آنها توجه ویژه داشت زیرا مقدار آنها در تابع هزینه تنظیم نمیشود.
مشتق مراتب بالاتر
اگر از تابع ![]() مشتق بگیریم چه اتفاقی میافتد؟ حاصل این مشتقگیری، مشتق مرتیه دوم خواهد بود که با
مشتق بگیریم چه اتفاقی میافتد؟ حاصل این مشتقگیری، مشتق مرتیه دوم خواهد بود که با ![]() ، یا
، یا ![]() نمایش داده میشود. اگر این فرآیند را با مشتقگیری از
نمایش داده میشود. اگر این فرآیند را با مشتقگیری از ![]() تکرار کنیم، مشتق مرتبه سوم
تکرار کنیم، مشتق مرتبه سوم ![]() یا
یا ![]() را به دست میآوریم. به همین طریق میتوانیم به مشتقگیری در مراتب بالاتر ادامه دهیم.
را به دست میآوریم. به همین طریق میتوانیم به مشتقگیری در مراتب بالاتر ادامه دهیم.
شهود پشت مشتق مرتبه دوم چیست؟ از آنجایی که مشتق (مرتبه اول) نرخ تغییر لحظهای تابع ![]() را در هر نقطه نشان میدهد، بنابراین مشتق مرتبهی دوم، نشاندهندهی نرخ تغییر لحظهای سرعت خود است؛ به عبارت دیگر، میتوانید آن را به عنوان شتاب در نظر بگیرید. اگر
را در هر نقطه نشان میدهد، بنابراین مشتق مرتبهی دوم، نشاندهندهی نرخ تغییر لحظهای سرعت خود است؛ به عبارت دیگر، میتوانید آن را به عنوان شتاب در نظر بگیرید. اگر ![]() ، آنگاه منحنی در حال شتاب گرفتن به سمت پایین است. اگر
، آنگاه منحنی در حال شتاب گرفتن به سمت پایین است. اگر ![]() باشد منحنی به سمت بالا شتاب میگیرد، و اگر
باشد منحنی به سمت بالا شتاب میگیرد، و اگر ![]() ، منحنی به صورت محلی، یک خط مستقیم است. توجه داشته باشید که یک منحنی میتواند به سمت بالا حرکت کند (یعنی
، منحنی به صورت محلی، یک خط مستقیم است. توجه داشته باشید که یک منحنی میتواند به سمت بالا حرکت کند (یعنی ![]() ) اما به سمت پایین شتاب بگیرد (یعنی
) اما به سمت پایین شتاب بگیرد (یعنی ![]() )برای مثال، مسیر یک سنگ را که به سمت بالا پرتاب میشود تصور کنید، که نیروی گرانش دائماً سنگ را به سمت پایین شتاب میدهد و در نتیجه، حرکت سنگ کند میشود.
)برای مثال، مسیر یک سنگ را که به سمت بالا پرتاب میشود تصور کنید، که نیروی گرانش دائماً سنگ را به سمت پایین شتاب میدهد و در نتیجه، حرکت سنگ کند میشود.
یادگیری عمیق معمولاً فقط از مشتقات مرتبه اول استفاده میکند، اما گاهی اوقات با برخی الگوریتمهای بهینهسازی یا توابع هزینه بر اساس مشتقات مرتبه دوم مواجه میشوید.
مشتقات جزیی
تا به اینجا، ما فقط توابعی را با یک متغیر ![]() در نظر گرفتهایم. وقتی چندین متغیر در تابع وجود دارد چه اتفاقی میافتد؟ برای مثال، اجازه دهید تا با یک تابع ساده با دو متغیر شروع کنیم:
در نظر گرفتهایم. وقتی چندین متغیر در تابع وجود دارد چه اتفاقی میافتد؟ برای مثال، اجازه دهید تا با یک تابع ساده با دو متغیر شروع کنیم:
اگر تابع ![]() را با استفاده از
را با استفاده از ![]() رسم کنیم، نمودار سه بعدی زیر را بدست میآوریم. همچنین یک نقطه
رسم کنیم، نمودار سه بعدی زیر را بدست میآوریم. همچنین یک نقطه ![]() را به همراه دو خط روی سطح نمودار رسم کردهایم که به زودی توضیح خواهیم داد.
را به همراه دو خط روی سطح نمودار رسم کردهایم که به زودی توضیح خواهیم داد.
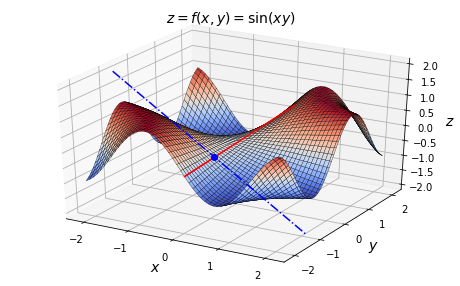
شکل 12: نمودار رویهی ![]()
اگر بخواهید روی این سطح در نقطه ![]() بایستید و در امتداد محور x به سمت راست (با افزایش
بایستید و در امتداد محور x به سمت راست (با افزایش ![]() ) قدم بردارید، مسیر شما به شدت پایین میرود (در امتداد خط آبی نقطهچین) زیرا شیب در امتداد این محور منفی خواهد بود. با این حال، اگر بخواهید در امتداد محور
) قدم بردارید، مسیر شما به شدت پایین میرود (در امتداد خط آبی نقطهچین) زیرا شیب در امتداد این محور منفی خواهد بود. با این حال، اگر بخواهید در امتداد محور ![]() ، به سمت عقب (افزایش
، به سمت عقب (افزایش ![]() ) قدم بزنید، مسیر شما تقریباً صاف خواهد بود (در امتداد خط قرمز). حداقل در دامنهی نمایش داده شده میتوان گفت: شیب در نقطهی
) قدم بزنید، مسیر شما تقریباً صاف خواهد بود (در امتداد خط قرمز). حداقل در دامنهی نمایش داده شده میتوان گفت: شیب در نقطهی ![]() و در امتداد خط قرمز رنگ، به میزان خیلی کمی مثبت است.
و در امتداد خط قرمز رنگ، به میزان خیلی کمی مثبت است.
همانطور که میبینید، دیگر صرفا یک عدد برای توصیف شیب تابع در یک نقطهی خاص کافی نیست. برای محور ![]() به یک شیب و برای محور
به یک شیب و برای محور ![]() یک شیب دیگر نیاز داریم. در واقع میخواهیم تا برای هر متغیر یک شیب جداگانه تعریف کنیم. برای یافتن شیب در امتداد محور
یک شیب دیگر نیاز داریم. در واقع میخواهیم تا برای هر متغیر یک شیب جداگانه تعریف کنیم. برای یافتن شیب در امتداد محور ![]() که مشتق جزئی تابع
که مشتق جزئی تابع ![]() نسبت به
نسبت به ![]() نامیده میشود، و با
نامیده میشود، و با ![]() نمایش داده میشود، میتوانیم از
نمایش داده میشود، میتوانیم از ![]() نسبت به
نسبت به ![]() مشتق بگیریم. در فرایند مشتقگیری همهی متغیرهای دیگر (در این مورد، فقط
مشتق بگیریم. در فرایند مشتقگیری همهی متغیرهای دیگر (در این مورد، فقط ![]() ) را به عنوان عدد ثابت در نظر میگیریم؛ بنابراین متغیرهای دیگر در فرایند مشتقگیری بیاثر میشوند.
) را به عنوان عدد ثابت در نظر میگیریم؛ بنابراین متغیرهای دیگر در فرایند مشتقگیری بیاثر میشوند.
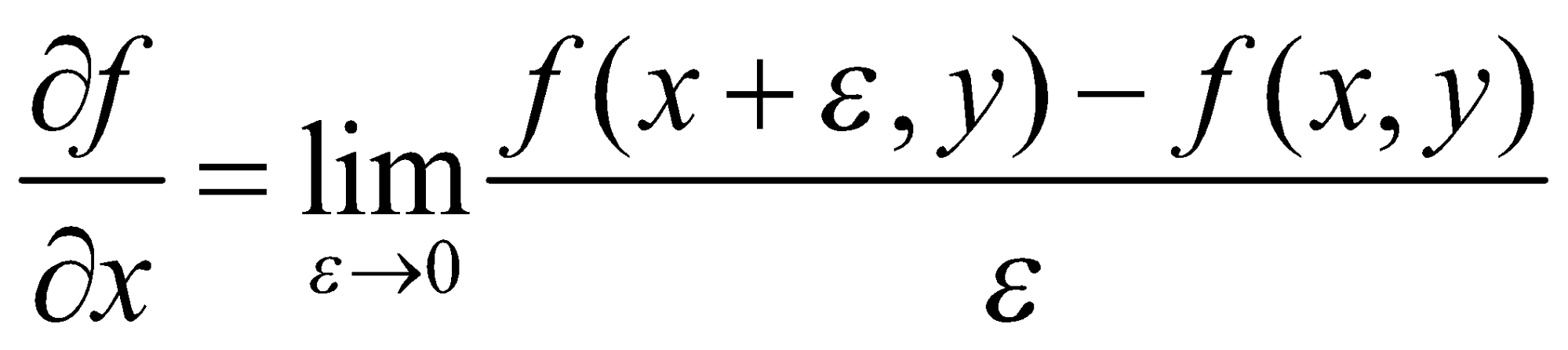
اگر از قواعد مشتقگیری موجود در جدول 1 استفاده کنید و![]() را به عنوان یک عدد ثابت در نظر بگیرید، آنگاه خواهید دید:
را به عنوان یک عدد ثابت در نظر بگیرید، آنگاه خواهید دید:
![]()
به طور مشابه، مشتق جزئی ![]() نسبت به
نسبت به ![]() به صورت زیر تعریف میشود:
به صورت زیر تعریف میشود:
![]()
با همهی متغیرها به جز ![]() مانند عددثابت رفتار میشود (در این مثال فقط
مانند عددثابت رفتار میشود (در این مثال فقط ![]() ). با استفاده از قواعد مشتقگیری، به دست میآوریم:
). با استفاده از قواعد مشتقگیری، به دست میآوریم:
![]()
اکنون معادلاتی برای محاسبهی شیب در امتداد محور ![]() و در امتداد محور
و در امتداد محور![]() داریم. اما در مورد سایر جهت ها چطور؟ اگر در نقطه
داریم. اما در مورد سایر جهت ها چطور؟ اگر در نقطه ![]() ، روی سطح رویهی سهبعدی ایستاده باشید، میتوانید تصمیم بگیرید که در هر جهتی که میخواهید راه بروید؛ نه فقط در امتداد محور
، روی سطح رویهی سهبعدی ایستاده باشید، میتوانید تصمیم بگیرید که در هر جهتی که میخواهید راه بروید؛ نه فقط در امتداد محور ![]() یا
یا ![]() . آن وقت شیب تابع در راستای دلخواه چقدر خواهد بود؟ آیا نباید بتوانیم شیب را در هر جهت ممکن محاسبه کنیم؟
. آن وقت شیب تابع در راستای دلخواه چقدر خواهد بود؟ آیا نباید بتوانیم شیب را در هر جهت ممکن محاسبه کنیم؟
میتوان نشان داد که اگر تمام مشتقات جزئی در یک همسایگی حول نقطهی ![]() تعریف شده و پیوسته باشند، تابع
تعریف شده و پیوسته باشند، تابع ![]() در آن نقطه کاملاً مشتقپذیر است؛ به این معنی که میتوان آن را در همسایگی نقطهی
در آن نقطه کاملاً مشتقپذیر است؛ به این معنی که میتوان آن را در همسایگی نقطهی ![]() با یک صفحه
با یک صفحه ![]() (صفحه مماس به سطح در همسایگی نقطهی
(صفحه مماس به سطح در همسایگی نقطهی![]() (تقریب زد. در این مورد، فقط داشتن مشتقات جزئی در امتداد محورهای اصلی (در مثال ما، محورهای
(تقریب زد. در این مورد، فقط داشتن مشتقات جزئی در امتداد محورهای اصلی (در مثال ما، محورهای ![]() و
و ![]() ) برای مشخص کردن کامل صفحهی مماس کافی است. معادله صفحه به صورت زیر است:
) برای مشخص کردن کامل صفحهی مماس کافی است. معادله صفحه به صورت زیر است:
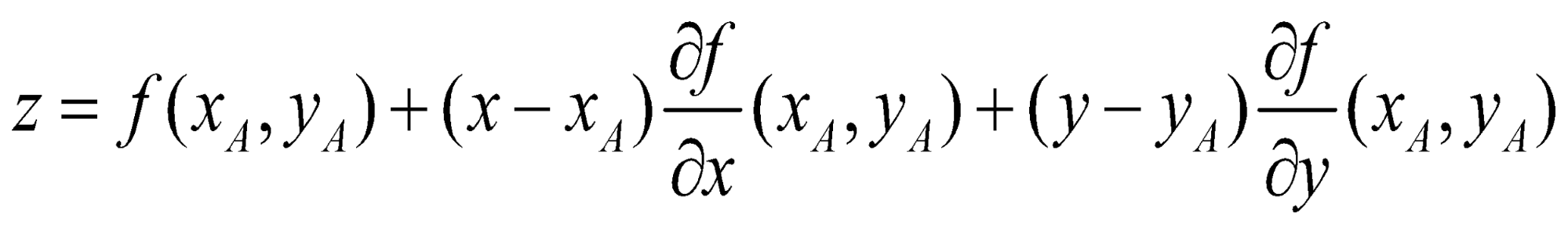
در یادگیری عمیق، ما معمولاً با توابع خوشرفتاری سروکار داریم که در هر نقطهی آن، تمام مشتقات جزئی تعریف شدهاند؛ بنابراین کاملاً مشتقپذیر هستند. اما باید بدانید که برخی از توابع تا آنچنان خوشرفتار نیستند. به عنوان مثال، تابع را در نظر بگیرید:
![]()
در مبدا مختصات (یعنی در ![]() ) مشتقات جزئی تابع
) مشتقات جزئی تابع ![]() با توجه به
با توجه به ![]() و
و ![]() هر دو کاملاً تعریف شده و برابر با 0 هستند. با این حال واضح است که تابع
هر دو کاملاً تعریف شده و برابر با 0 هستند. با این حال واضح است که تابع ![]() نمیتواند با یک صفحه در آن نقطه تقریب زدهشود. تابع
نمیتواند با یک صفحه در آن نقطه تقریب زدهشود. تابع ![]() در آن نقطه کاملاً مشتقپذیر نیست (اما در هر نقطه از محورها کاملاً مشتقپذیر است).
در آن نقطه کاملاً مشتقپذیر نیست (اما در هر نقطه از محورها کاملاً مشتقپذیر است).
بردار گرادیان
تا کنون فقط توابعی با یک متغیر ![]() ، و یا با دو متغیر
، و یا با دو متغیر ![]() و
و ![]() در نظر گرفتهایم؛ اما مطالب پاراگراف قبلی برای توابعی با متغیرهای بیشتر نیز کاربرد دارد. بنابراین بیایید تابع
در نظر گرفتهایم؛ اما مطالب پاراگراف قبلی برای توابعی با متغیرهای بیشتر نیز کاربرد دارد. بنابراین بیایید تابع ![]() با
با ![]() متغیر را در نظر بگیریم:
متغیر را در نظر بگیریم: ![]() .
.
برای راحتی کار، بردار ![]() را تعریف میکنیم که اجزای آن، این متغیرها هستند:
را تعریف میکنیم که اجزای آن، این متغیرها هستند:
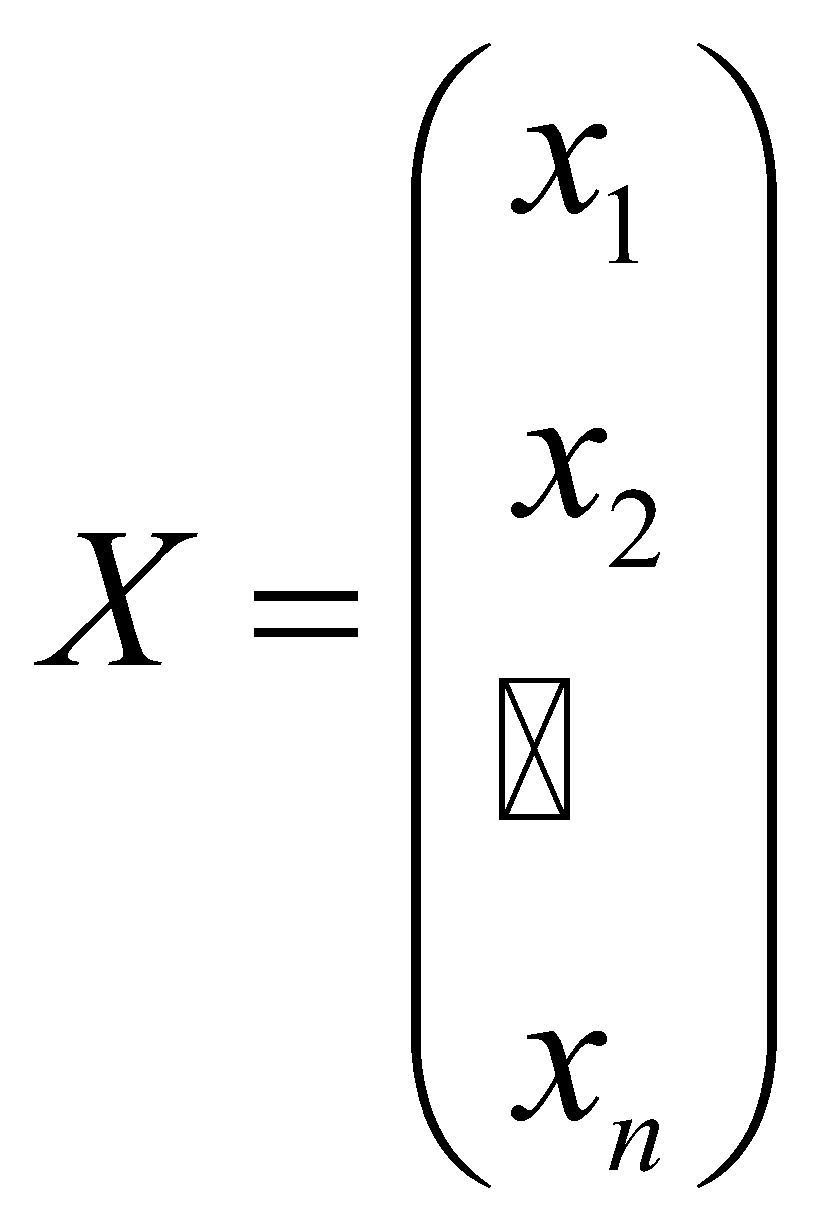
حالا میتوانیم برای راحتی به جای ![]() بنویسیم
بنویسیم ![]() .
.
گرادیان تابع ![]() در نقطهی
در نقطهی ![]() برداری است که اجزای آن، همهی مشتقات جزئی تابع در آن نقطه هستند. گرادیان در نقطهی
برداری است که اجزای آن، همهی مشتقات جزئی تابع در آن نقطه هستند. گرادیان در نقطهی ![]() را با
را با ![]() یا گاهی
یا گاهی![]() نمایش میدهند:
نمایش میدهند:
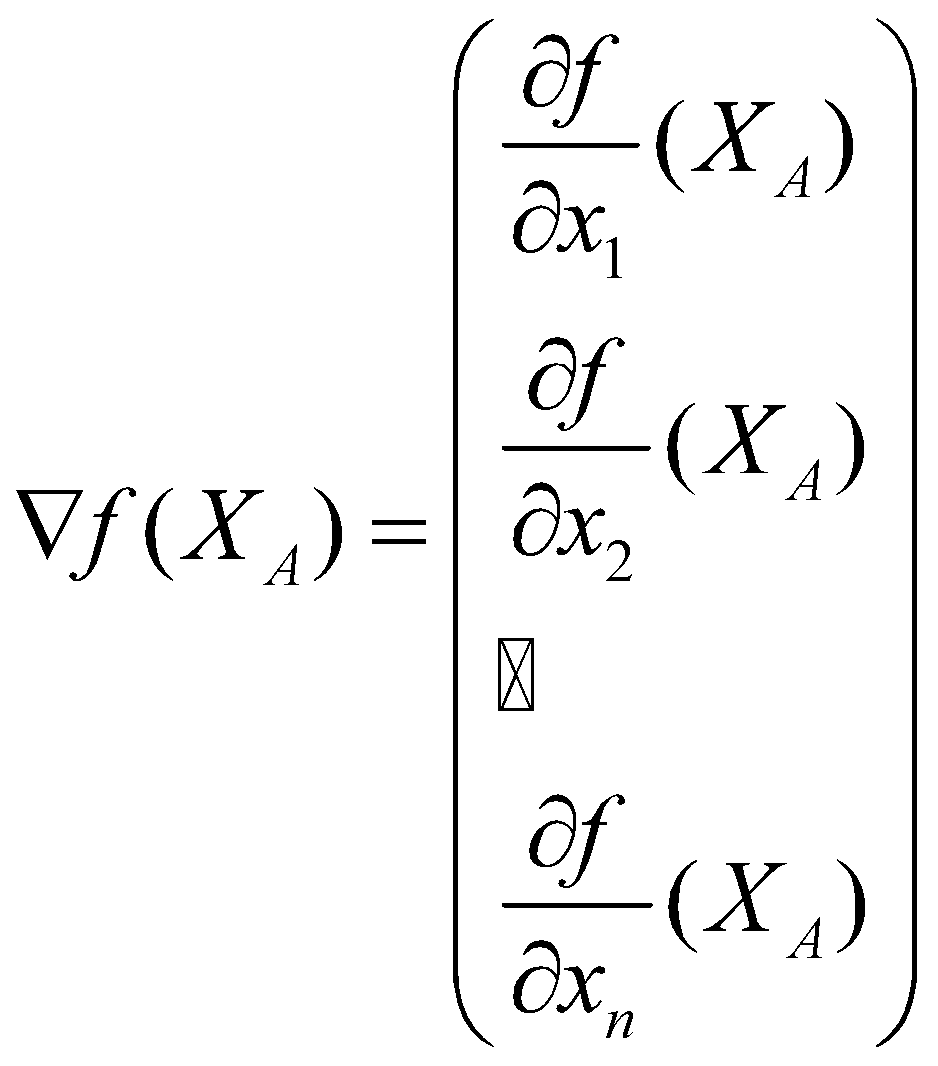
با فرض اینکه تابع در نقطه ![]() کاملاً مشتقپذیر است، سطحی که توصیف میکند را میتوان با صفحهای مماس در آن نقطه تقریب زد (همانطور که در بخش قبل بحث شد)، و بردار گرادیان، برداری است که به سمت تندترین شیب در آن صفحه اشاره میکند.
کاملاً مشتقپذیر است، سطحی که توصیف میکند را میتوان با صفحهای مماس در آن نقطه تقریب زد (همانطور که در بخش قبل بحث شد)، و بردار گرادیان، برداری است که به سمت تندترین شیب در آن صفحه اشاره میکند.
گرادیان کاهشی (نسخهی کامل)
در یادگیری عمیق، الگوریتم گرادیان کاهشی که قبلاً در مورد آن صحبت کردیم، به جای مشتقات بر پایه گرادیان اجرا میشود (به همین دلیل نام آن گرادیان کاهشی است). روش کار تقریبا مشابه است؛ اما از بردارها به جای اسکالرها استفاده میکنیم. با یک بردار تصادفی ![]() شروع میکنیم، سپس گرادیان تابع
شروع میکنیم، سپس گرادیان تابع ![]() را در آن نقطه محاسبه میکنیم، و یک گام کوچک در جهت مخالف آن حرکت میکنیم. این فرایند را تا همگرایی الگوریتم تکرار میکنیم. به طور دقیق تر، در مرحلهی
را در آن نقطه محاسبه میکنیم، و یک گام کوچک در جهت مخالف آن حرکت میکنیم. این فرایند را تا همگرایی الگوریتم تکرار میکنیم. به طور دقیق تر، در مرحلهی ![]() ،
، ![]() را محاسبه میکنیم. ثابت
را محاسبه میکنیم. ثابت ![]() نرخ یادگیری است که معمولاً مقدار کمی مانند 0.001 را به آن میدهیم. ما در عمل معمولاً از انواع کارآمدتر این الگوریتم استفاده میکنیم، اما ایدهی کلی همان چیزی است که مطرح کردیم.
نرخ یادگیری است که معمولاً مقدار کمی مانند 0.001 را به آن میدهیم. ما در عمل معمولاً از انواع کارآمدتر این الگوریتم استفاده میکنیم، اما ایدهی کلی همان چیزی است که مطرح کردیم.
در یادگیری عمیق، حرف ![]() به طور کلی برای نمایش دادههای ورودی استفاده میشود. وقتی از یک مدل شبکه عصبی برای پیشبینی استفاده میکنید، ورودیهای
به طور کلی برای نمایش دادههای ورودی استفاده میشود. وقتی از یک مدل شبکه عصبی برای پیشبینی استفاده میکنید، ورودیهای ![]() را به مدل میدهید و پیشبینی
را به مدل میدهید و پیشبینی ![]() را دریافت میکنید. تابع
را دریافت میکنید. تابع ![]() با پارامترهای مدل به عنوان عدد ثابت رفتار میکند. میتوانیم با نوشتن
با پارامترهای مدل به عنوان عدد ثابت رفتار میکند. میتوانیم با نوشتن ![]() نمایش دهیم که منظور از
نمایش دهیم که منظور از ![]() ، پارامترهای مدل است که تابع در محاسبات به آنها متکی است اما آنها را به عنوان ثابت در نظر میگیرد و نه متغیر.
، پارامترهای مدل است که تابع در محاسبات به آنها متکی است اما آنها را به عنوان ثابت در نظر میگیرد و نه متغیر.
با این حال، هنگام آموزش یک شبکه عصبی، کاملا برعکس عمل میکنیم: تمام نمونههای آموزشی در ماتریس ![]() قرار میگیرند؛ همهی برچسبها در بردار
قرار میگیرند؛ همهی برچسبها در بردار ![]() مشخص میشوند.
مشخص میشوند. ![]() و
و ![]() هر دو به عنوان ثابت در نظر گرفته میشوند، در حالی که
هر دو به عنوان ثابت در نظر گرفته میشوند، در حالی که ![]() به عنوان متغیر در نظر گرفته میشود. به طور خاص، ما سعی میکنیم تابع هزینهی
به عنوان متغیر در نظر گرفته میشود. به طور خاص، ما سعی میکنیم تابع هزینهی ![]() را به حداقل برسانیم.
را به حداقل برسانیم. ![]() تابعی است که اختلاف بین پیشبینیهای
تابعی است که اختلاف بین پیشبینیهای ![]() و برچسبهای واقعی
و برچسبهای واقعی ![]() را اندازه میگیرد که در آن
را اندازه میگیرد که در آن ![]() بردار حاوی پیشبینیهای مربوط به هر نمونهی آموزشی را نشان میدهد. کمینه کردن تابع هزینه معمولاً با استفاده از الگوریتم گرادیان کاهشی یا یک روش مشابه و برپایهی آن انجام میشود یعنی: با پارامترهای تصادفی مدل
بردار حاوی پیشبینیهای مربوط به هر نمونهی آموزشی را نشان میدهد. کمینه کردن تابع هزینه معمولاً با استفاده از الگوریتم گرادیان کاهشی یا یک روش مشابه و برپایهی آن انجام میشود یعنی: با پارامترهای تصادفی مدل ![]() شروع میکنیم، سپس
شروع میکنیم، سپس ![]() را محاسبه میکنیم و از این بردار گرادیان برای انجام یک مرحله کاهش گرادیان استفاده میکنیم، سپس این فرایند را تا همگرایی روند، تکرار میکنیم. این نکته بسیار مهم است که درک کنیم که گرادیان تابع هزینه با توجه به پارامترهای مدل
را محاسبه میکنیم و از این بردار گرادیان برای انجام یک مرحله کاهش گرادیان استفاده میکنیم، سپس این فرایند را تا همگرایی روند، تکرار میکنیم. این نکته بسیار مهم است که درک کنیم که گرادیان تابع هزینه با توجه به پارامترهای مدل ![]() انجام میشود و نه ورودیهای مدل
انجام میشود و نه ورودیهای مدل ![]() .
.
ماتریس ژاکوبی
تاکنون فقط توابعی را در نظر گرفتهایم که یک اسکالر را خروجی میدهند، اما توابع میتوانند به جای عدد، خروجی برداری داشته باشند. به عنوان مثال، یک شبکه عصبی طبقهبندی معمولاً برای هر کلاس، یک احتمال خروجی میدهد. بنابراین اگر ![]() کلاس وجود داشته باشد، شبکه عصبی یک بردار
کلاس وجود داشته باشد، شبکه عصبی یک بردار ![]() بعدی برای هر نمونه خروجی میدهد.
بعدی برای هر نمونه خروجی میدهد.
در یادگیری عمیق معمولاً فقط باید تابع هزینه را متمایز کنیم، که تقریباً همیشه یک عدد اسکالر را خروجی میدهد. اما برای یک ثانیه فرض کنید که میخواهید از تابع ![]() که بردارهای
که بردارهای ![]() بعدی خروجی میدهد، مشتقگیری کنید. خبر خوب این است که شما میتوانید با هر یک از ابعاد خروجی مستقل از سایر ابعاد رفتار کنید. منظور این است که از مشتقگیری جزئی برای هر بعد ورودی و خروجی استفاده کنیم. اگر همه مشتقات را در یک ماتریس قرار دهید، به طوری که هر بعد ورودی در یک ستون و هر بعد خروجی در یک ردیف ماتریس قرار بگیرد، شما ماتریس ژاکوبی را خواهید داشت.
بعدی خروجی میدهد، مشتقگیری کنید. خبر خوب این است که شما میتوانید با هر یک از ابعاد خروجی مستقل از سایر ابعاد رفتار کنید. منظور این است که از مشتقگیری جزئی برای هر بعد ورودی و خروجی استفاده کنیم. اگر همه مشتقات را در یک ماتریس قرار دهید، به طوری که هر بعد ورودی در یک ستون و هر بعد خروجی در یک ردیف ماتریس قرار بگیرد، شما ماتریس ژاکوبی را خواهید داشت.
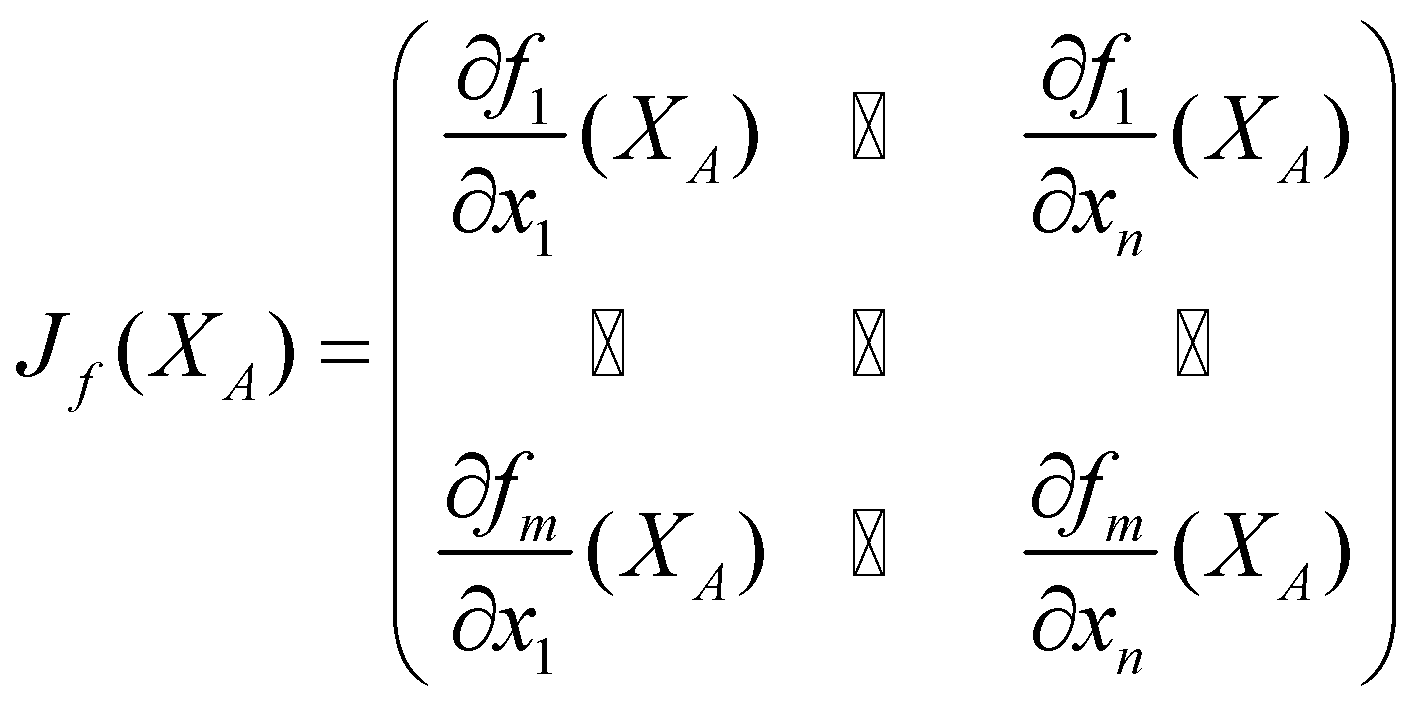
خود مشتقات جزئی تابع اغلب ژاکوبی نامیده میشوند. ماتریس ژاکوبی فقط مشتقات جزئی مرتبه اول تابع ![]() است.
است.
ماتریس Hessian
بیایید به تابع ![]() برگردیم که یک بردار
برگردیم که یک بردار ![]() بعدی را به عنوان ورودی میگیرد و یک اسکالر را به عنوان خروجی برمیگرداند. اگر معادلهی مشتق جزئی
بعدی را به عنوان ورودی میگیرد و یک اسکالر را به عنوان خروجی برمیگرداند. اگر معادلهی مشتق جزئی ![]() را با توجه به
را با توجه به ![]() (جزء
(جزء ![]() ام
ام ![]() (تعیین کنید، تابع جدیدی از
(تعیین کنید، تابع جدیدی از ![]() خواهید داشت:
خواهید داشت: ![]() . سپس میتوانید مشتق جزئی این تابع را با توجه به
. سپس میتوانید مشتق جزئی این تابع را با توجه به ![]() (جزء
(جزء ![]() ام
ام ![]() (محاسبه کنید. نتیجه یک مشتق جزئی از مشتق جزئی
(محاسبه کنید. نتیجه یک مشتق جزئی از مشتق جزئی ![]() است. به عبارت دیگر، خروجی، مشتق جزئی مرتبه دوم است که به آن هسین نیز می گویند. درایههای ماتریس هسین به فرم
است. به عبارت دیگر، خروجی، مشتق جزئی مرتبه دوم است که به آن هسین نیز می گویند. درایههای ماتریس هسین به فرم ![]() هستند که درایههای غیرقطری آن
هستند که درایههای غیرقطری آن ![]() و در درایههای قطری،
و در درایههای قطری، ![]() است. به درایههای غیرقطری ماتریس هسین، مشتقات جزئی مرتبه دوم مختلط میگویند زیرا در آنها از تابع
است. به درایههای غیرقطری ماتریس هسین، مشتقات جزئی مرتبه دوم مختلط میگویند زیرا در آنها از تابع ![]() نسبت به دو متغیر متفاوت مشتقگیری انجام میشود.
نسبت به دو متغیر متفاوت مشتقگیری انجام میشود.
بیایید تابع ![]() را بررسی کنیم. همانطور که قبلا نشان دادیم، مشتقات جزئی مرتبه اول
را بررسی کنیم. همانطور که قبلا نشان دادیم، مشتقات جزئی مرتبه اول ![]() عبارتند از:
عبارتند از: ![]() و .
و .![]() بنابراین اکنون میتوانیم تمام درایههای ماتریس هسین متناظر این تابع را به کمک قواعد مشتقگیری که پیشتر راجع به آنها صحبت کردیم، به دست بیاوریم.
بنابراین اکنون میتوانیم تمام درایههای ماتریس هسین متناظر این تابع را به کمک قواعد مشتقگیری که پیشتر راجع به آنها صحبت کردیم، به دست بیاوریم.
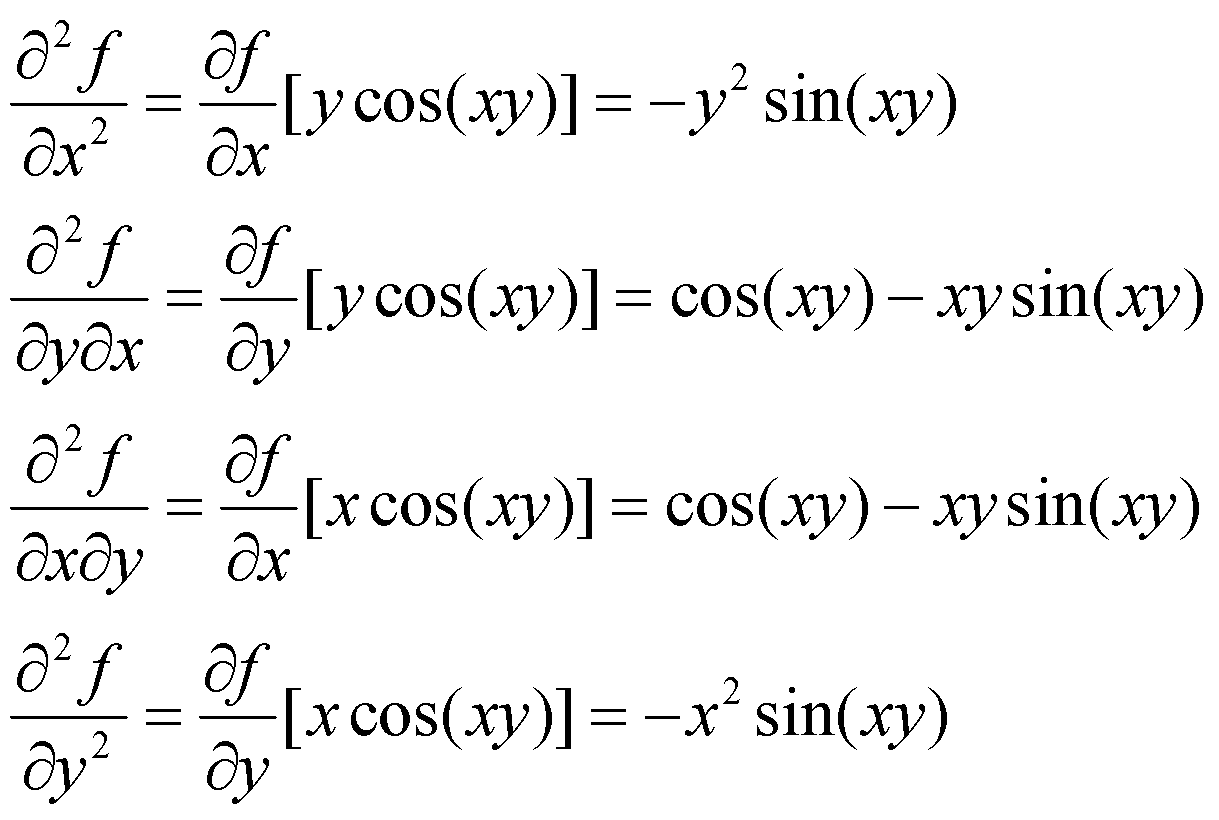
توجه داشته باشید که در روابط بالا 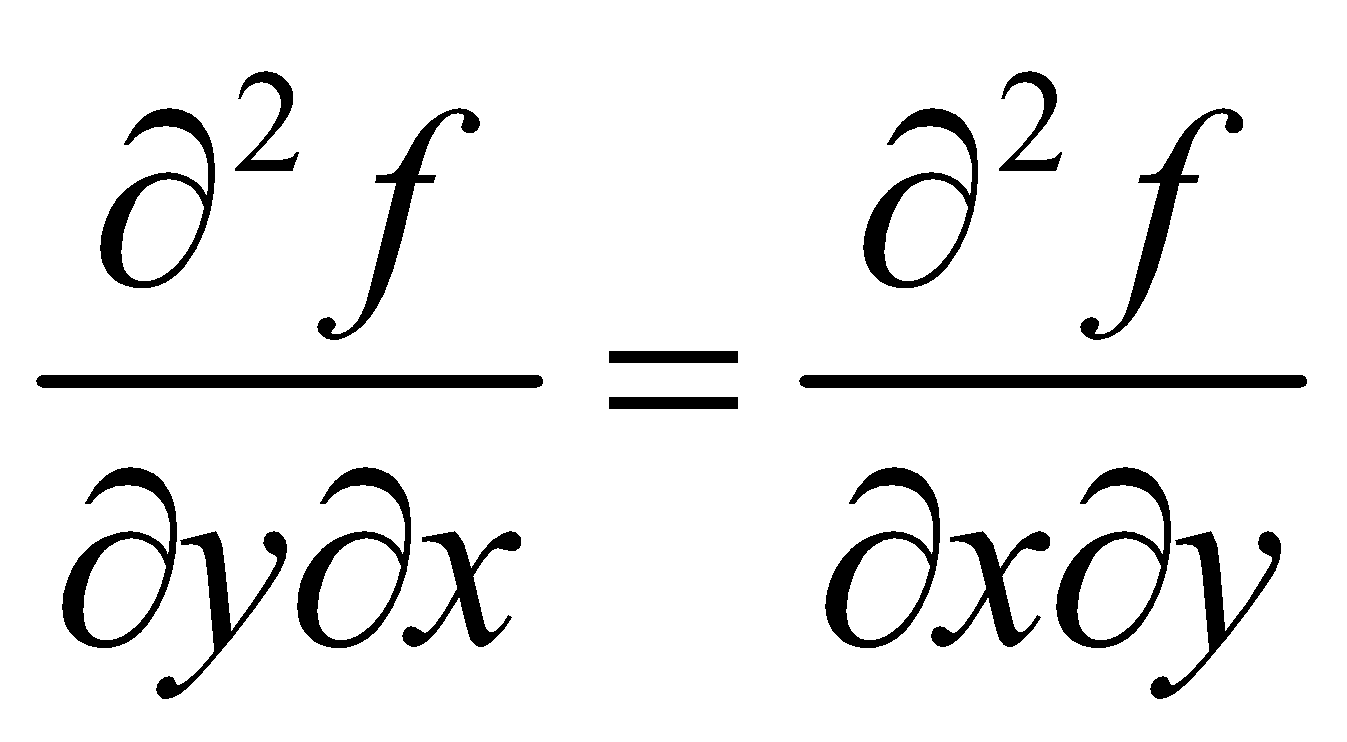 . این اتفاق زمانی میافتد که تمام مشتقات جزئی در یک همسایگی در اطراف نقطهای که در آن از تابع مشتق میگیریم، تعریفشده و پیوسته باشند.
. این اتفاق زمانی میافتد که تمام مشتقات جزئی در یک همسایگی در اطراف نقطهای که در آن از تابع مشتق میگیریم، تعریفشده و پیوسته باشند.
ماتریس هسین به فرم زیر خواهد بود:
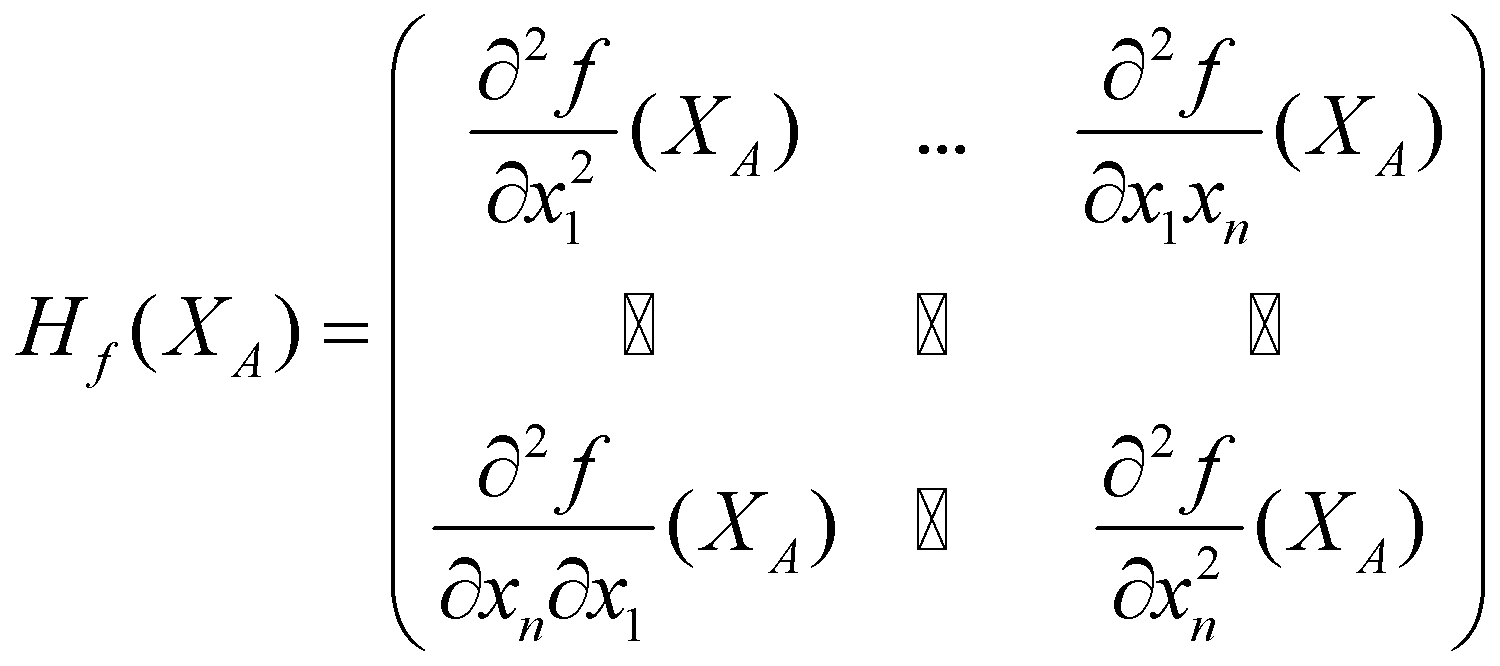
الگوریتمهای بهینهسازی بسیار خوبی وجود دارند که بر پایههای هسینها طراحی شدهاند اما در یادگیری عمیق تقریباً هرگز از آنها استفاده نمیکنیم. در واقع، اگر یک تابع ![]() متغیر داشته باشد،
متغیر داشته باشد، ![]() هسین خواهد داشت. از آنجا که شبکههای عصبی معمولاً چندین میلیون پارامتر دارند، تعداد هسینها حتی از هزاران میلیارد فراتر خواهد رفت. بنابراین حتی اگر مقدار رم لازم را داشته باشیم، محاسبات بسیار کند خواهد شد.
هسین خواهد داشت. از آنجا که شبکههای عصبی معمولاً چندین میلیون پارامتر دارند، تعداد هسینها حتی از هزاران میلیارد فراتر خواهد رفت. بنابراین حتی اگر مقدار رم لازم را داشته باشیم، محاسبات بسیار کند خواهد شد.
مثال
یک) تابع نمایی مرکب
![]()
تابع نمایی یک مثال بسیار اساسی، رایج و مفید در ریاضیات است. این تابع کاملاً مثبت است، یعنی در ![]() همواره
همواره ![]() . ویژگی مهم دیگر این تابع این است که
. ویژگی مهم دیگر این تابع این است که ![]() علاوهبراین، باید به خاطر داشته باشید که تابع نمایی، معکوس تابع لگاریتمی است. همچنین این تابع یکی از سادهترین توابع برای مشتقگیری است زیرا مشتق آن نیز تابع نمایی است یعنی
علاوهبراین، باید به خاطر داشته باشید که تابع نمایی، معکوس تابع لگاریتمی است. همچنین این تابع یکی از سادهترین توابع برای مشتقگیری است زیرا مشتق آن نیز تابع نمایی است یعنی ![]() . هنگامی که تابع نمایی با یک تابع دیگر ترکیب شود، مشتقگیری کمی متفاوت میشود. در چنین مواردی از فرمول قانون زنجیرهای استفاده میکنیم که بیان میکند مشتق
. هنگامی که تابع نمایی با یک تابع دیگر ترکیب شود، مشتقگیری کمی متفاوت میشود. در چنین مواردی از فرمول قانون زنجیرهای استفاده میکنیم که بیان میکند مشتق ![]() برابر با
برابر با ![]() است، یعنی:
است، یعنی:
![]()
با اعمال قانون زنجیرهای، میتوانیم مشتق ![]() را محاسبه کنیم:
را محاسبه کنیم:
![]()
دو) تابع با پایهی متغیر و توان متغیر
مهمترین چیزی که هنگام بررسی یک تابع نمایی به فرم بالا باید در نظر داشت، اولا، رابطه معکوس بین تابع نمایی و تابع لگاریتمی است؛ و دوما، این نکته که هر تابع نماییای را میتوان به فرم یک تابع نمایی طبیعی به شکل زیر بازنویسی کرد.
![]()
قبل از اینکه به مثال ![]() خود برسیم، اجازه دهید این ویژگی را با تابع سادهتر
خود برسیم، اجازه دهید این ویژگی را با تابع سادهتر ![]() نشان دهیم. ابتدا از معادلهی بالا برای بازنویسی
نشان دهیم. ابتدا از معادلهی بالا برای بازنویسی ![]() به صورت
به صورت ![]() استفاده می کنیم و سپس قانون زنجیرهای را روی آن اعمال میکنیم.
استفاده می کنیم و سپس قانون زنجیرهای را روی آن اعمال میکنیم.
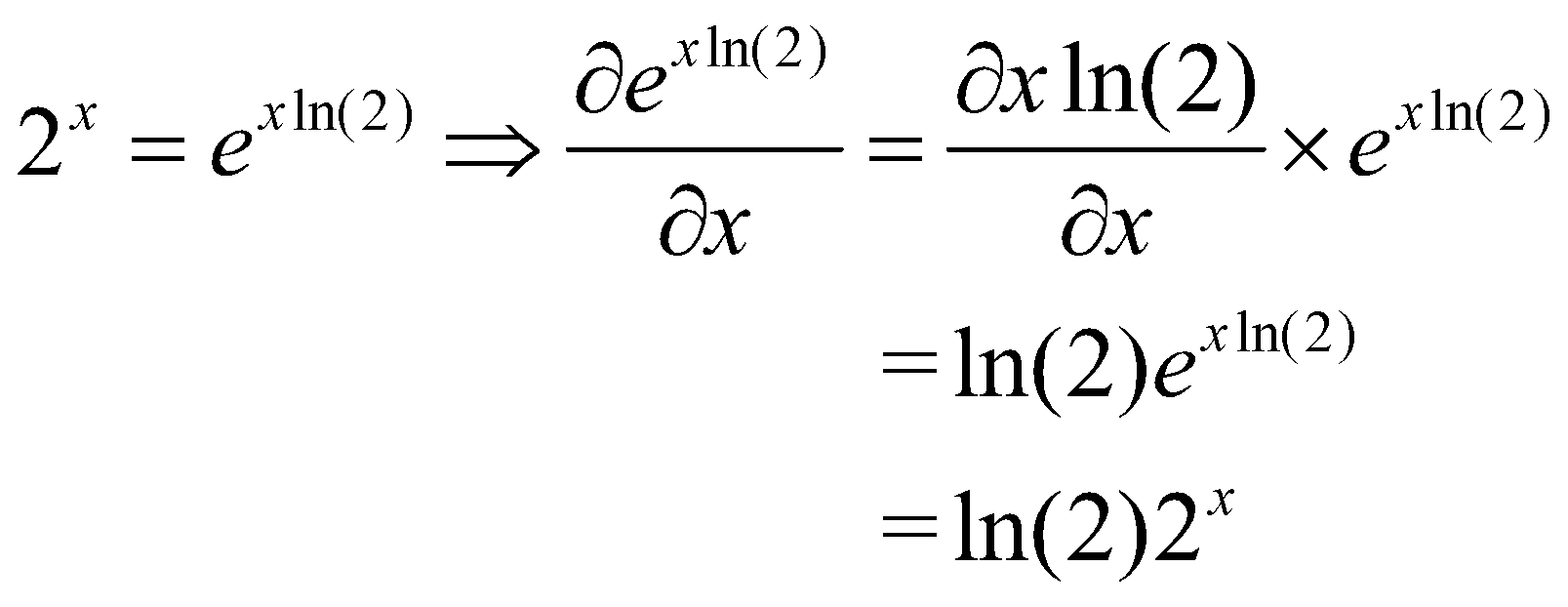
برگردیم به تابع ![]() . هنگامی که تابع را به صورت
. هنگامی که تابع را به صورت ![]() بازنویسی میکنیم، مشتقگیری نسبتاً ساده میشود و تنها بخش دشوار آن مرحلهی اعمال قانون زنجیرهای است.
بازنویسی میکنیم، مشتقگیری نسبتاً ساده میشود و تنها بخش دشوار آن مرحلهی اعمال قانون زنجیرهای است.
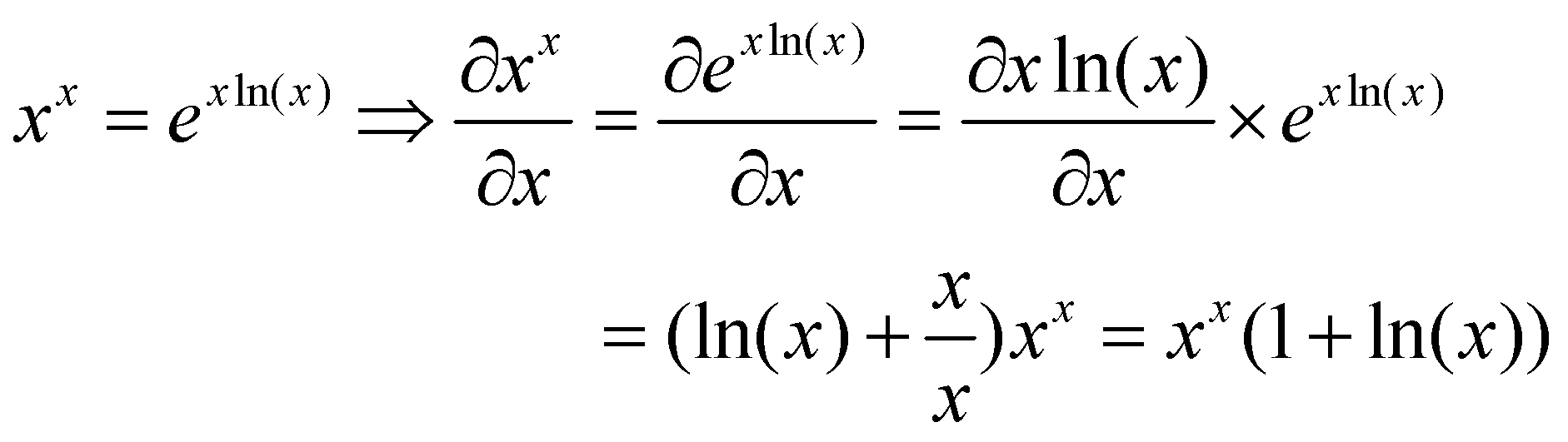
توجه داشته باشید که در اینجا از قانون مشتقگیری عبارت ضربی ![]() در محاسبهی مشتق عبارت
در محاسبهی مشتق عبارت ![]() بهره بردیم.
بهره بردیم.
تابع ![]() معمولاً بدون هیچ اطلاعاتی در مورد دامنهی تابع مورد سوال قرار میگیرد. اینجاست که سوال جالب میشود. بدون مشخص کردن دامنهی تابع، به نظر میرسد که
معمولاً بدون هیچ اطلاعاتی در مورد دامنهی تابع مورد سوال قرار میگیرد. اینجاست که سوال جالب میشود. بدون مشخص کردن دامنهی تابع، به نظر میرسد که ![]() برای هر مقادیر مثبت و منفی تعریف شده است. با این حال، برای مقادیر منفی
برای هر مقادیر مثبت و منفی تعریف شده است. با این حال، برای مقادیر منفی ![]() ، به عنوان مثال،
، به عنوان مثال، ![]() ، خروجی تابع یک عدد مختلط است (
، خروجی تابع یک عدد مختلط است (![]() ). یک راه دور زدن مختلط بودن خروجی تابع این است که دامنه تابع را به صورت
). یک راه دور زدن مختلط بودن خروجی تابع این است که دامنه تابع را به صورت ![]() تعریف کنیم. اما تابع روی این دامنه نیز همچنان برای مقادیر منفی مشتقپذیر نخواهد بود. بنابراین برای اینکه تابع
تعریف کنیم. اما تابع روی این دامنه نیز همچنان برای مقادیر منفی مشتقپذیر نخواهد بود. بنابراین برای اینکه تابع ![]() در کل دامنه مشتقپذیر باشد، باید دامنهی تابع را به مقادیر کاملاً مثبت محدود کنیم.
در کل دامنه مشتقپذیر باشد، باید دامنهی تابع را به مقادیر کاملاً مثبت محدود کنیم.
ما ![]() را از دامنه حذف میکنیم زیرا برای اینکه مشتق در نقطهی
را از دامنه حذف میکنیم زیرا برای اینکه مشتق در نقطهی ![]() تعریف شود، نیاز داریم که حد مشتق از سمت چپ (محدود در
تعریف شود، نیاز داریم که حد مشتق از سمت چپ (محدود در ![]() برای مقادیر منفی) برابر با حد مشتق از سمت راست (محدود در
برای مقادیر منفی) برابر با حد مشتق از سمت راست (محدود در ![]() برای مقادیر مثبت) باشد. این شرط در این مساله نقض شده است. از آنجا که حد چپ
برای مقادیر مثبت) باشد. این شرط در این مساله نقض شده است. از آنجا که حد چپ ![]() تعریف نشده است، تابع در
تعریف نشده است، تابع در ![]() مشتقپذیر نیست و بنابراین دامنهی تابع فقط به مقادیر مثبت محدود میشود.
مشتقپذیر نیست و بنابراین دامنهی تابع فقط به مقادیر مثبت محدود میشود.
قبل از اینکه به بخش بعدی برویم، یک نسخهی کمی پیچیدهتر از این تابع را برای آزمایش درک شما مطرح میکنیم: 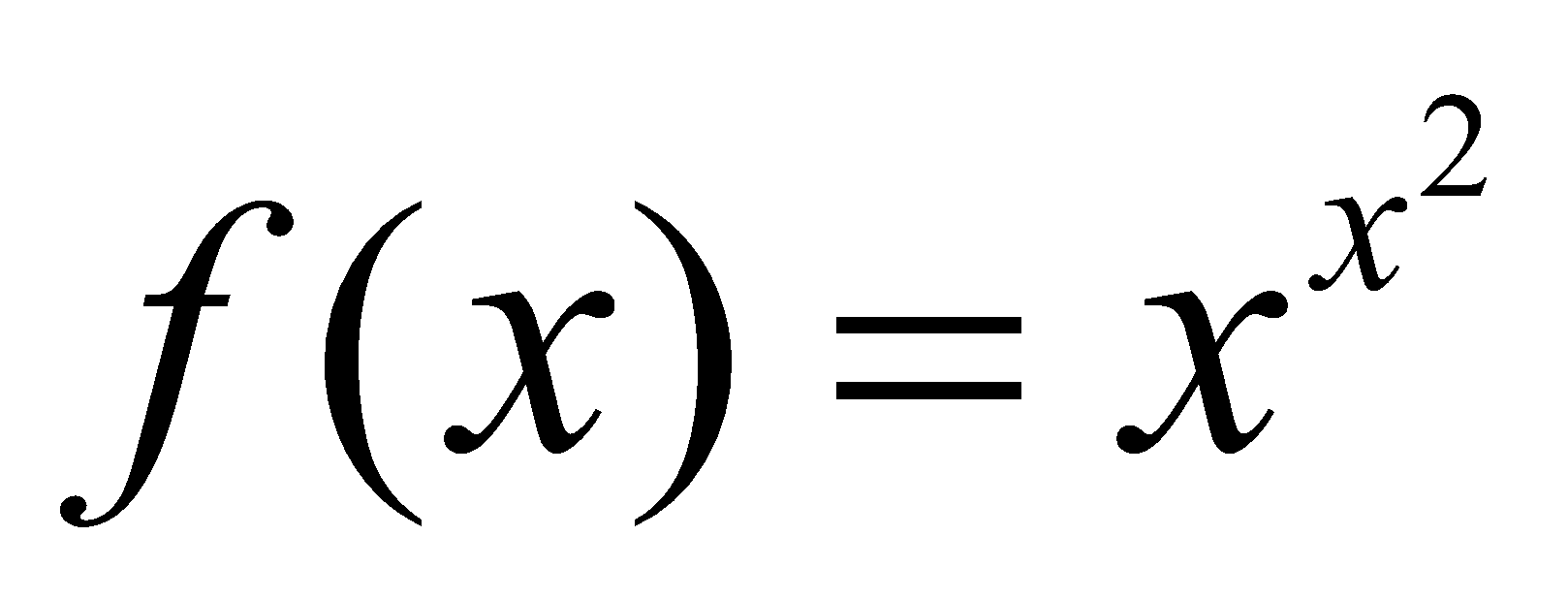 . اگر منطق و مراحل طیشده در مثال قبلی را فهمیده باشید، اضافه کردن یک عببارت توانی اضافی نباید مشکلی ایجاد کند و باید نتیجه زیر را به دست آورید:
. اگر منطق و مراحل طیشده در مثال قبلی را فهمیده باشید، اضافه کردن یک عببارت توانی اضافی نباید مشکلی ایجاد کند و باید نتیجه زیر را به دست آورید:
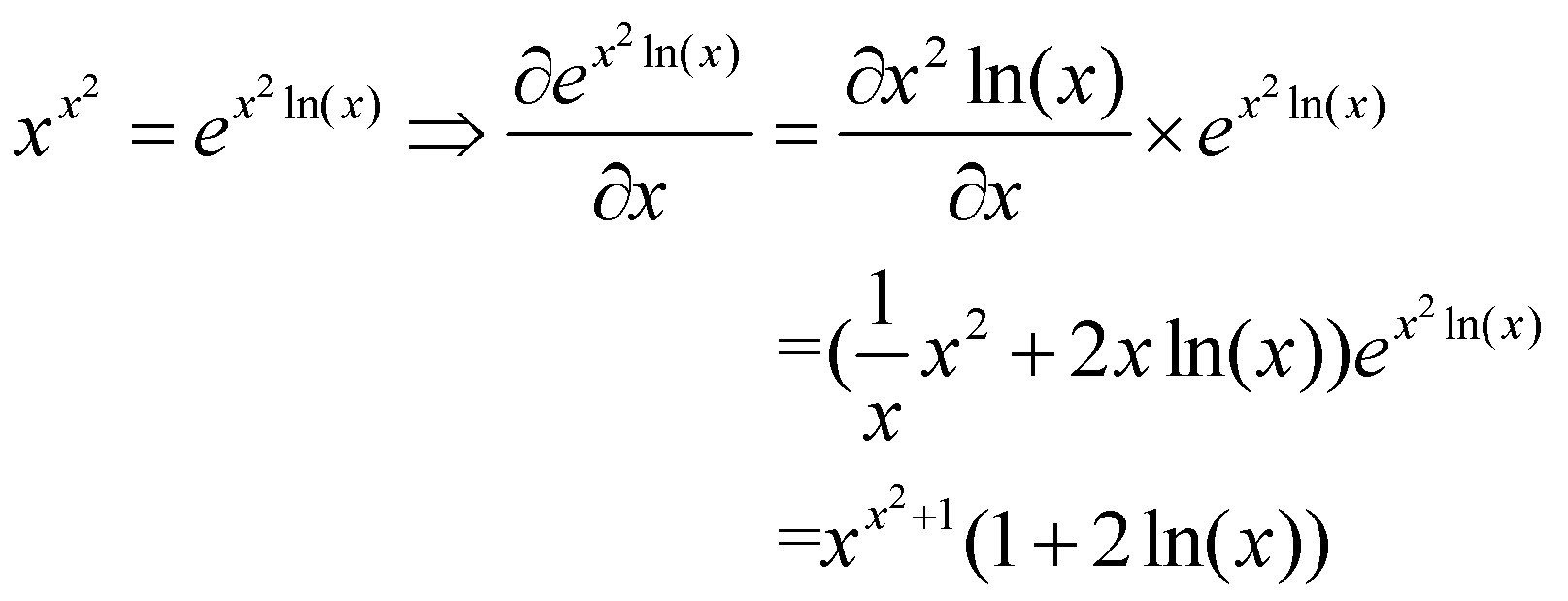
سه) گرادیان تابع با ورودی چندبعدی
![]()
تا اینجا، توابع مورد بحث در مثالهای پیشین، توابع از ![]() به
به ![]() بودند. یعنی دامنه و برد تابع اعداد حقیقی هستند. اما در یادگیری ماشین اساساً با بردارها کار میکنیم و توابعی که مورد استفاده هستند، چندبعدی هستند. یک مثال خوب از این توابع، یک لایه مدل شبکهی عصبی با ورودی
بودند. یعنی دامنه و برد تابع اعداد حقیقی هستند. اما در یادگیری ماشین اساساً با بردارها کار میکنیم و توابعی که مورد استفاده هستند، چندبعدی هستند. یک مثال خوب از این توابع، یک لایه مدل شبکهی عصبی با ورودی ![]() بعدی و خروجی
بعدی و خروجی ![]() بعدی است؛ یعنی
بعدی است؛ یعنی ![]() . این تابع در واقع یک ترکیب خطی از
. این تابع در واقع یک ترکیب خطی از ![]() است که در آن
است که در آن ![]() بردار وزن و
بردار وزن و ![]() بردار ورودی است.
بردار ورودی است. ![]() تابع فعالساز است که یک نگاشت غیرخطی را بر روی عبارت داخل پرانتز پیاده میکند. در حالت کلی، میتوان کل دامنهی
تابع فعالساز است که یک نگاشت غیرخطی را بر روی عبارت داخل پرانتز پیاده میکند. در حالت کلی، میتوان کل دامنهی ![]() را با چنین تبدیلی به
را با چنین تبدیلی به ![]() نگاشت کرد.
نگاشت کرد.
در مورد خاص  ، مشتق را گرادیان می نامند. بیایید مشتق تابع سهبعدی زیر را که
، مشتق را گرادیان می نامند. بیایید مشتق تابع سهبعدی زیر را که ![]() را به
را به ![]() نگاشت میکند، محاسبه کنیم:
نگاشت میکند، محاسبه کنیم:
![]()
شما میتوانید این تابع را یک نگاشت که بردار به اندازهی ![]() را به بردار اندازهی
را به بردار اندازهی ![]() تبدیل میکند، در نظر بگیرید.
تبدیل میکند، در نظر بگیرید.
مشتق تابع با ورودی چندبعدی، تابع گرادیان ![]() نامیده میشود که
نامیده میشود که ![]() را به
را به ![]() نگاشت میکند. تابع گرادیان مجموعهای از مشتقات جزئی است که در آن، هر کدام از مشتقات جزئی، تابعی از
نگاشت میکند. تابع گرادیان مجموعهای از مشتقات جزئی است که در آن، هر کدام از مشتقات جزئی، تابعی از ![]() متغیر هستند.
متغیر هستند.
برای یافتن گرادیان تابع ![]() ، یک بردار از مشتقات جزئی
، یک بردار از مشتقات جزئی ![]() ،
، ![]() و
و ![]() را میسازیم و نتیجهی زیر را به دست میآوریم:
را میسازیم و نتیجهی زیر را به دست میآوریم:
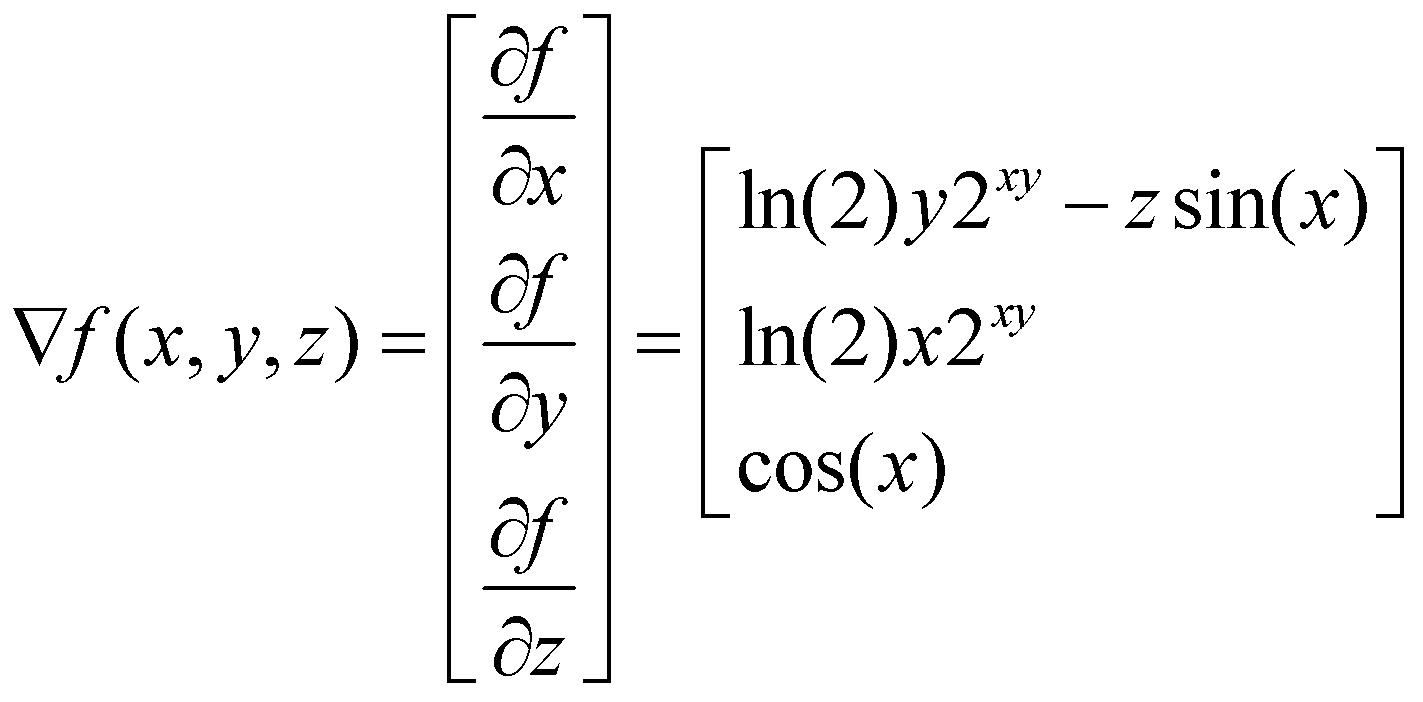
توجه داشته باشید که این مثال، مشابه مثال قبلی است بنابراین از رابطهی ![]() استفاده میکنیم.
استفاده میکنیم.
در نتیجه، برای یک تابع با ورودی چندبعدی که ![]() را به
را به ![]() نگاشت میکند، مشتق یک گرادیان است که
نگاشت میکند، مشتق یک گرادیان است که ![]() را به
را به ![]() نگاشت میکند.
نگاشت میکند.
در حالت کلی، برای یک تابع چندبعدی از ![]() به
به ![]() که در آن
که در آن ![]() ، مشتق تابع که یک ماتریس ژاکوبی است (به جای بردار گرادیان). در بخش بعدی این موضوع را بررسی میکنیم.
، مشتق تابع که یک ماتریس ژاکوبی است (به جای بردار گرادیان). در بخش بعدی این موضوع را بررسی میکنیم.
چهار) ماتریس ژاکوبی تابع با ورودی و خروجی چندبعدی
![]()
از بخش قبل میدانیم که مشتق تابعی که ![]() را به
را به ![]() نگاشت میکند، یک بردار گرادیان از
نگاشت میکند، یک بردار گرادیان از ![]() به
به ![]() است. اما در موردی که برد (خروجی) تابع نیز چندبعدی است، یعنی نگاشت از
است. اما در موردی که برد (خروجی) تابع نیز چندبعدی است، یعنی نگاشت از ![]() به
به ![]() برای
برای ![]() ، چه اتفاقی میافتد؟
، چه اتفاقی میافتد؟
در چنین حالتی، مشتق تابع، ماتریس ژاکوبی خواهد بود. میتوانیم بردار گرادیان را به سادگی به عنوان یک حالت خاص از ماتریس ژاکوبی با ابعاد ![]() در نظر بگیریم که در آن،
در نظر بگیریم که در آن،![]() برابر با تعداد متغیرها است. ماتریس ژاکوبی تابع
برابر با تعداد متغیرها است. ماتریس ژاکوبی تابع ![]() ، ورودی
، ورودی![]() را به
را به![]() نگاشت میکند. بنابراین ژاکوبی، ماتریسی با ابعاد
نگاشت میکند. بنابراین ژاکوبی، ماتریسی با ابعاد ![]() است. به عبارت دیگر، سطر
است. به عبارت دیگر، سطر ![]() ام
ام ![]() نشان دهندهی گرادیان
نشان دهندهی گرادیان ![]() زیرتابع (تابع تحدید شدهی
زیرتابع (تابع تحدید شدهی ![]() )
) ![]() از
از![]() است.
است.
بیایید تابع ![]() را بررسی کنیم که یک نگاشت از
را بررسی کنیم که یک نگاشت از ![]() به
به ![]() است؛ بنابراین هم ورودی و هم خروجی تابع، چندبعدی هستند. از آنجایی که تابع ریشهی دوم برای مقادیر منفی تعریف نشده است، باید دامنه
است؛ بنابراین هم ورودی و هم خروجی تابع، چندبعدی هستند. از آنجایی که تابع ریشهی دوم برای مقادیر منفی تعریف نشده است، باید دامنه ![]() را به
را به ![]() محدود کنیم. سطر اول ماتریس ژاکوبی، گرادیان تابع اول، یعنی
محدود کنیم. سطر اول ماتریس ژاکوبی، گرادیان تابع اول، یعنی ![]() ، و سطر دوم ماتریس، گرادیان تابع دوم، یعنی
، و سطر دوم ماتریس، گرادیان تابع دوم، یعنی![]() خواهد بود.
خواهد بود.
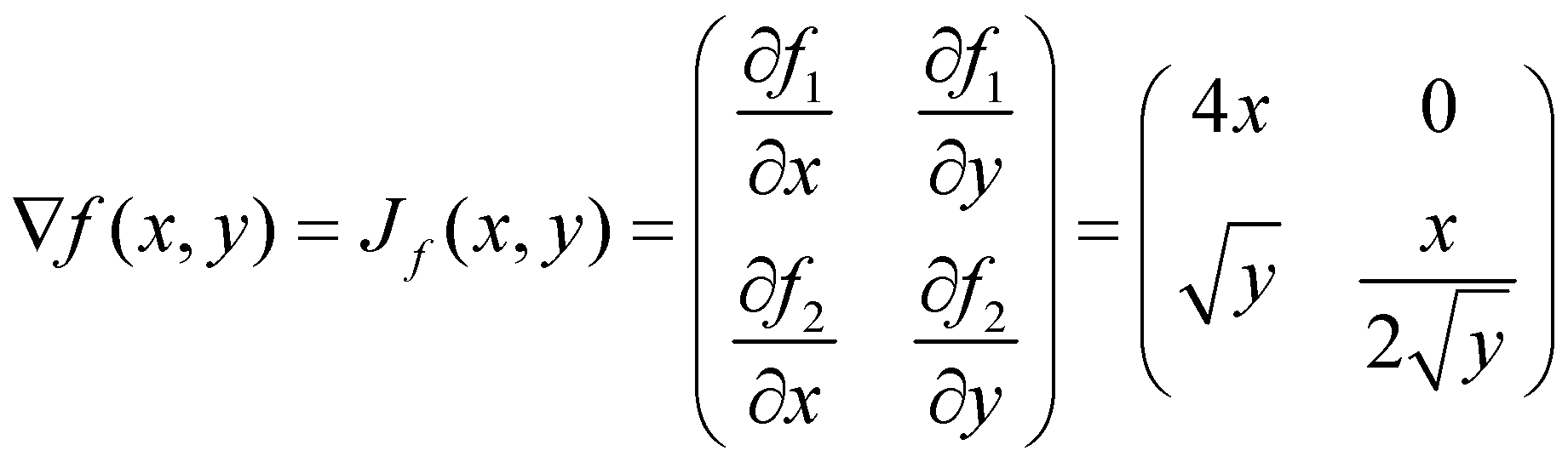
در یادگیری عمیق، یک مثال مناسب برای کاربرد ماتریس ژاکوبی، در زمینهی توضیحپذیری (مانند شبکههای عصبی مبتنی بر حساسیت) است. هدف این مدلها، درک رفتار شبکههای عصبی و بررسی حساسیت لایهی خروجی شبکهی عصبی نسبت به ورودی مدل است. ماتریس ژاکوبی به ما کمک میکند تا تأثیر تغییرات ویژگیهای ورودی مدل را بر خروجی مدل مشاهده کنیم. این رویکرد را میتوان به طور مشابه برای درک آنچه که در لایههای میانی مدل شبکهی عصبی میگذرد، به کار برد.
به طور خلاصه، به یاد داشته باشید که در حالی که گرادیان، مشتق یک تابع با خروجی یکبعدی نسبت به یک بردار است، ماتریس ژاکوبی مشتق یک تابع با خروجی چندبعدی نسبت به یک بردار است.
پنج) ماتریس هسین تابع با ورودی چندبعدی
![]()
تا کنون، در مثالها بر مشتقات مرتبه اول متمرکز بودهایم، اما در شبکههای عصبی، گاهی به مشتقات مرتبه بالاتر توابع چندبعدی برمیخوریم. یک مورد ویژهی آن، مشتق دوم است که آن را ماتریس هسین مینامیم و با ![]() یا
یا ![]() نشان میدهیم. برای تابع
نشان میدهیم. برای تابع ![]() که از
که از ![]() به
به ![]() است،
است، ![]() نگاشتی از
نگاشتی از ![]() به
به ![]() است.
است.
بیایید تحلیل کنیم که چگونه از خروجی ![]() به
به ![]() رسیدیم. مشتق مرتبه اول، یعنی گرادیان، یک نگاشت از
رسیدیم. مشتق مرتبه اول، یعنی گرادیان، یک نگاشت از ![]() به
به ![]() است و مشتق آن یک ژاکوبی است. بنابراین گرادیان هر زیرتابع (تابع تحدید شده) منجر به یک نگاشت از
است و مشتق آن یک ژاکوبی است. بنابراین گرادیان هر زیرتابع (تابع تحدید شده) منجر به یک نگاشت از ![]() به
به ![]() میشود. میدانیم که
میشود. میدانیم که ![]() زیرتابع وجود دارد (یکی به ازای هر بعد)، پس میتوانید به این فکر کنید که گویی مشتق هر عنصر از بردار گرادیان، یک بردار خواهد بود، بنابراین از کنار هم قرار دادن این بردارها، یک ماتریس به دست میآید.
زیرتابع وجود دارد (یکی به ازای هر بعد)، پس میتوانید به این فکر کنید که گویی مشتق هر عنصر از بردار گرادیان، یک بردار خواهد بود، بنابراین از کنار هم قرار دادن این بردارها، یک ماتریس به دست میآید.
برای محاسبه هسین باید مشتقات متقاطع را محاسبه کنیم، یعنی ابتدا نسبت به ![]() و سپس نسبت به
و سپس نسبت به ![]() یا برعکس مشتقگیری کنیم. ممکن است بپرسید که آیا ترتیب مشتقگیری متقاطع اهمیت دارد یا خیر؟ به عبارت دیگر، آیا ماتریس هسین متقارن است یا نه. در مواردی که تابع
یا برعکس مشتقگیری کنیم. ممکن است بپرسید که آیا ترتیب مشتقگیری متقاطع اهمیت دارد یا خیر؟ به عبارت دیگر، آیا ماتریس هسین متقارن است یا نه. در مواردی که تابع![]() دو بار به صورت پیوسته قابل مشتقگیری است، قضیهی شوارتز بیان میکند که مشتقات متقاطع برابر هستند و بنابراین ماتریس هسین متقارن است.
دو بار به صورت پیوسته قابل مشتقگیری است، قضیهی شوارتز بیان میکند که مشتقات متقاطع برابر هستند و بنابراین ماتریس هسین متقارن است.
ساختن هسین یک تابع برابر است با یافتن مشتقات جزئی مرتبه دوم یک تابع. برای مثال، برای تابع![]() ، داریم:
، داریم:
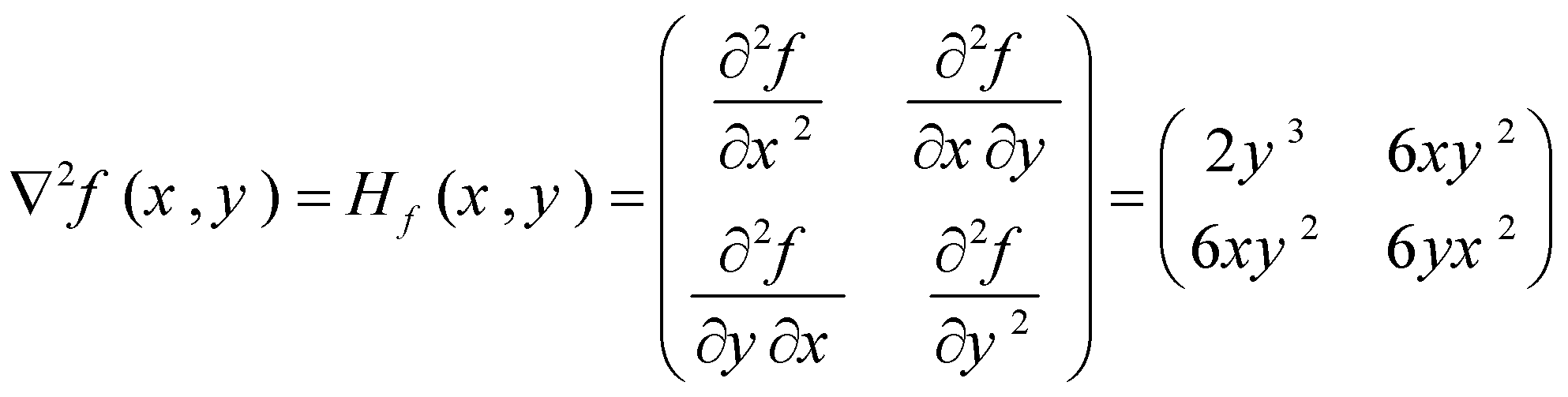
همانطور که میبینید، مشتقات متقاطع برابر هستند. ابتدا با توجه به ![]() مشتق گرفتیم و
مشتق گرفتیم و ![]() را به دست آوردیم. سپس نسبت به
را به دست آوردیم. سپس نسبت به ![]() مشتق گرفتیم و به
مشتق گرفتیم و به ![]() رسیدیم. در عناصر روی قطر اصلی، نسبت به یک متغیر، دو بار مشتق میگیریم.
رسیدیم. در عناصر روی قطر اصلی، نسبت به یک متغیر، دو بار مشتق میگیریم.
در ادامه میتوانیم به مشتقات مرتبه دوم برای توابع چندبعدی که ![]() را به
را به ![]() نگاشت میکنند، فکر کنیم که به طور شهودی میتواند به عنوان یک ژاکوبی مرتبه دوم دیده شود. حاصل، یک نگاشت از
نگاشت میکنند، فکر کنیم که به طور شهودی میتواند به عنوان یک ژاکوبی مرتبه دوم دیده شود. حاصل، یک نگاشت از ![]() به
به ![]() خواهد بود، یعنی یک تنسور سهبعدی. مشابه هسین، برای یافتن گرادیان ژاکوبی (مشتقگیری مرتبه دوم)، از هر عنصر از ماتریس
خواهد بود، یعنی یک تنسور سهبعدی. مشابه هسین، برای یافتن گرادیان ژاکوبی (مشتقگیری مرتبه دوم)، از هر عنصر از ماتریس ![]() مشتق میگیریم و ماتریسی از بردارها، یعنی یک تنسور به دست میآوریم. اگرچه بعید است که از شما خواسته شود چنین محاسباتی را به صورت دستی انجام دهید، اما مهم است که از نحوهی محاسبهی مشتقات مرتبه بالاتر برای توابع چندبعدی آگاه باشید.
مشتق میگیریم و ماتریسی از بردارها، یعنی یک تنسور به دست میآوریم. اگرچه بعید است که از شما خواسته شود چنین محاسباتی را به صورت دستی انجام دهید، اما مهم است که از نحوهی محاسبهی مشتقات مرتبه بالاتر برای توابع چندبعدی آگاه باشید.
نظرات