مروری بر جبر خطی: اسکلت داده‌ها - قسمت دوم

مقدمه

در قسمت اول با بردارها و برخی اعمال هندسی که بر آن‌ها اعمال می‌شود آشنا شدیم. در این قسمت به سراغ ماتریس‌ها می‌رویم که از کنار هم قرار دادن بردارها حاصل می‌شوند و با برخی ویژگی‌های آن‌ها که در یادگیری ماشین مورد استفاده قرار می‌گیرند آشنا می‌شویم.

ماتریس‌ها

ماتریس‌ها نقش اصلی را در جبر خطی ایفا می‌کنند. آنها را می‌توان برای نمایش سیستم‌های معادلات خطی استفاده کرد. همچنین می‌توان از آن‌ها برای نمایش توابع خطی (نگاشت‌های خطی) استفاده کرد. قبل از اینکه درباره برخی از این موضوعات جالب بحث کنیم، بیایید ابتدا تعریف کنیم که ماتریس چیست و چه نوع عملیاتی را می توانیم با ماتریس‌ها انجام دهیم.

ماتریس یک آرایش از اعداد حقیقی است که دارای  سطر و  ستون است و به فرم زیر نمایش داده می‌شود:

وقتی راجع به تنها یک سطر یا یک ستون صحبت می‌کنیم، می‌توانیم آن را یک بردار بنامیم. در واقع یک ماتریس، مجموعه‌ای از بردارهای کنار هم قرار گرفته است.

جمع ماتریسی

اگر دو ماتریس  و  هم‌بعد باشند؛ یعنی تعداد سطرها و ستون‌های برابر داشته باشند، جمع‌پذیر هستند. عملیات جمع به صورت درایه به درایه و به صورت زیر انجام می‌شود:

ضرب ماتریسی

در ابتدا باید بگوییم که ضرب ماتریسی خاصیت جابجایی ندارد یعنی:

در ضمن هر دو ماتریس دلخواه را نمی‌توان در هم ضرب کرد. برای این که دو ماتریس ضرب‌پذیر باشند، باید تعداد ستون‌های ماتریس اول، برابر با تعداد سطرهای ماتریس دوم باشد.

تعداد سطرهای ماتریس حاصل از ضرب ماتریسی، برابر با تعداد سطرهای ماتریس اول، و تعداد ستون‌های آن، برابر با تعداد ستون‌های ماتریس دوم است.

اگر  و ، داریم:

که هر درایه‎‌ی آن به صورت زیر تعریف می‌شود:

در واقع برای به دست آوردن هر درایه‌ی ماتریس حاصل ضرب، یک سطر از ماتریس اول را در یک ستون از ماتریس دوم، درایه به درایه ضرب می‌کنیم و در نهایت آن‌ها را با هم جمع می‌کنیم. در هندسه‌ی تحلیلی به این فرایند ضرب داخلی یا ضرب نقطه‌ای گفته می‌شود.

توجه داشته باشید که همان طور که در رابطه‌ی بالا مشخص است، ضرب ماتریسی یک ضرب درایه به درایه نیست یعنی:

در برخی مسائل، مخصوصا در برنامه‌نویسی گاهی پیش می‌آید که دو ماتریس را درایه به درایه ضرب کنیم که به آن، ضرب هادامارد می‌گویند.

بنابراین اگر یک ماتریس  و یک ماتریس  داشته باشیم، اگر اولی را در دومی ضرب ماتریسی کنیم، حاصل آن یک ماتریس  خواهد بود و اگر دومی را در اولی ضرب کنیم، ماتریس حاصل ضرب،  خواهد بود.

اگر تعداد سطر و ستون یک ماتریس با هم برابر باشد، به آن ماتریس مربعی می‌گوییم.

اگر درایه‌های روی قطر یک ماتریس مربعی تماما برابر با 1 باشند و تمام درایه‌های دیگر برابر با 0 باشند، به آن ماتریس، ماتریس همانی می‌گوییم مه به فرم زیر است:

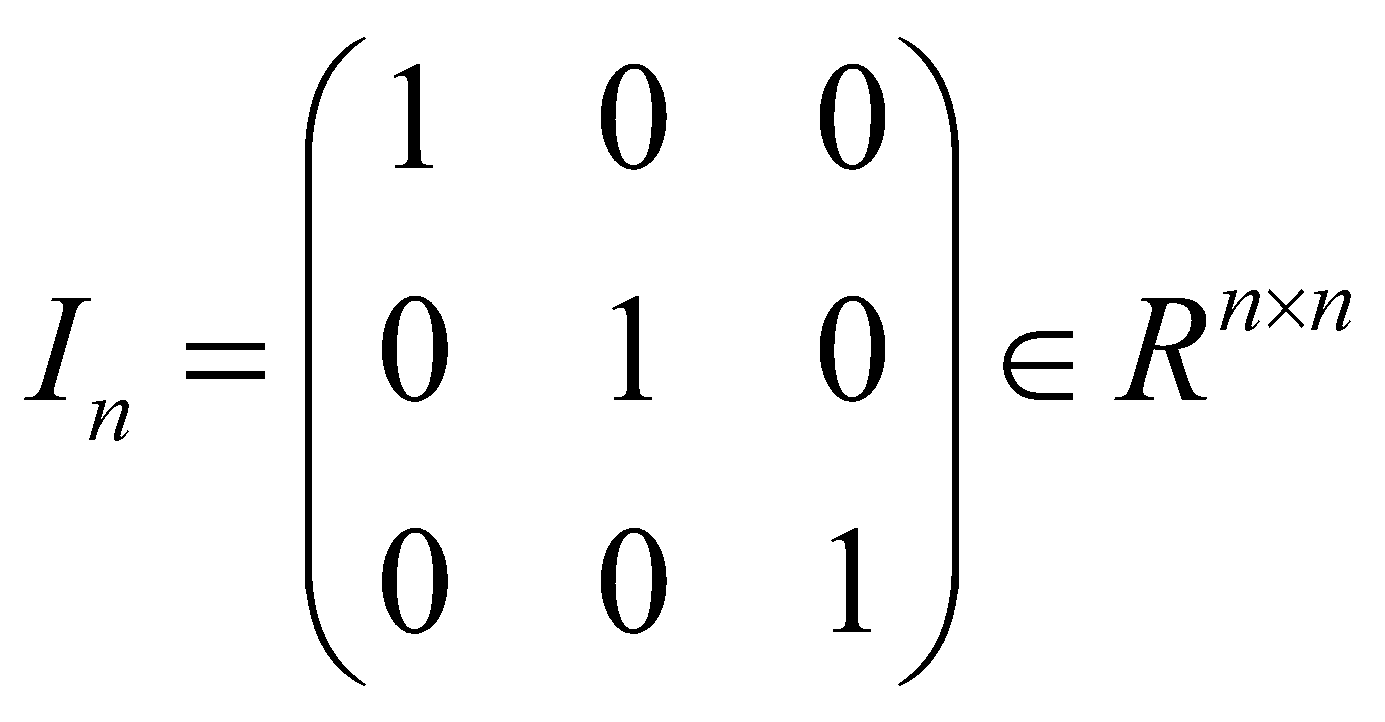
حالا که جمع و ضرب ماتریسی و همچنین ماتریس همانی را معرفی کرده‌ایم، می‌توانیم چند خاصیت را درباره‌ی ماتریس‌ها بیان کنیم:

معکوس ماتریس

ماتریس مربعی  را در نظر بگیرید. فرض کنید ماتریس  وجود دارد به قسمی که . در این شرایط ماتریس  معکوس ماتریس  نامیده می‌شود که آن را با  نمایش می‌دهیم.

توجه داشته باشید که لزوما همه‌ی ماتریس‌ها دارای معکوس نیستند. اگر ماتریسی دارای معکوس باشد، به آن معکوس‌پذیر می‌گوییم. توجه داشته باشید که معکوس ماتریس همواره یکتاست.

معکوس ماتریس

ماتریس زیر را در نظر بگیرید:

اگر  را در ماتریس زیر ضرب کنیم:

خواهیم داشت:

بنابراین معکوس ماتریس به صورت زیر خواهد بود:

همان‌طور که ملاحظه می‌کنید، معکوس ماتریس  وجود دارد اگر و تنها اگر . جلوتر خواهیم دید که  در واقع دترمینان ماتریس        است. بنابراین به صورت کلی می‌توانیم برای بررسی معکوس‌پذیر بودن ماتریس، به دترمینان ماتریس مراجعه کنیم.

مثال

ماتریس‌های  و  معکوس یکدیگرند بنابراین .

ترانهاده‌ی ماتریس

برای ماتریس ، به ماتریس  که هر درایه‌ی آن به صورت  مشخص می‌شود، ترانهاده‌ی ماتریس   می‌گوییم و آن را به صورت  نمایش می‌دهیم.

به صورت کلی ترانهاده‌ی یک ماتریس را می‌توان با قرار دان ستون‌های ماتریس به جای سطرهای آن، به دست آورد.

برخی روابط مربوط به ترانهاده‌ی ماتریس را با هم مرور می‌کنیم:

اگر ترانهاده‌ی ماتریس مربعی  با خودش برابر باشد، به ماتریس  متقارن می‌گوییم.

اگر ماتریس مربعی معکوس‌‌پذیر باشد، ترانهاده‌ی آن نیز معکوس‌پذیر است و داریم:

حاصل جمع دو ماتریس متقارن، همواره متقارن است اما حاصل ضربشان لزوما متقارن نیست.

ضرب عدد در ماتریس

ماتریس  و اسکالر  را در نظر بگیرید. در این صورت، با ضرب اسکالر در ماتریس به صورت ، داریم: . یعنی اسکالر در هر درایه‌ی ماتریس ضرب می‌شود.

به ازای  و  عضو اعداد حقیقی داریم:

برای مثال

اگر قرار دهیم:

به ازای هر مقدار دلخواه حقیقی برای  و  داریم:

پایه‌ی ماتریس

ما قبلا بردارها و برخی اعمال اصلی که روی آن‌ها پیاده می‌شود را بررسی کرده‌ایم.

به بردارها و مجموعه اعمال قابل اعمال روی آن‌ها، یک فضای برداری گفته می‌شود. البته فضای برداری تعریف دقیق ریاضیاتی دارد که در اینجا هدف ما نیست.

اگر چند بردار را انتخاب کنیم، هر کدام را در یک اسکالر ضرب کنیم و سپس حاصل را با هم جمع کنیم، آنگاه یک ترکیب خطی از بردارها را خواهیم داشت. یعنی اگر ، تعدادی بردار باشند و  تعدادی اسکالر حقیقی باشند، به عبارت  ترکیب خطی از  می‌گوییم.

اگر برای ، تنها جواب معادله‌ی ،  باشد، می‌گوییم بردارهای  مستقل خطی هستند. در غیر این صورت وابسته‌ی خطی خواهند بود.

از ترکیب خطی بردارهای مستقل خطی، می‌توان بردارهای وابسته‌ی خطی ایجاد کرد.

به کوچک‌ترین مجموعه بردارهای مستقل خطی که توانایی ساختن کل فضای برداری را داشته باشند، پایه‌ی فضای برداری می‌گوییم.

مجموعه‌ی پایه یکتا نیست اما تمام مجموعه‌های پایه به اندازه‌ی همدیگر عضو دارند.

به عنوان مثال در فضای ، تمامی بردارهای موجود در فضای برداری را می‌توان به کمک یک ترکیب خطی از بردارهای یکه‌ی  و  به دست آورد.

در واقع بردارهای  و  پایه‌های فضای برداری هستند. می‌توانید یک مجموعه پایه‌ی دیگر برای این فضا معرفی کنید؟

همان‌طور که می‌دانید، سطرها و ستون‌های ماتریس در واقع بردار هستند.

مجموعه پایه‌ی یک ماتریس را تعریف می‌کنیم تعداد سطرهای ماتریس که سطرهای دیگر، وابسته‌ی خطی آن‌ها هستند. یعنی سطرهای وابسته‌ی خطی براساس سطرهای مستقل خطی قابل بیان هستند.

رتبه‌ی ماتریس

مشابه مطالبی که در قسمت قبلی در مورد سطرهای مستقل خطی گفتیم، در مورد ستون‌های ماتریس نیز وجود دارد.

نکته‌ی جالب این است که تعداد ستون‌های مستقل خطی ماتریس دقیقا به تعداد سطرهای مستقل خطی ماتریس یا همان پایه‌ها است.

به تعداد ستون‌های مستقل خطی ماتریس، رتبه‌ی ماتریس می‌گویند.

برخی خواص رتبه‌ی ماتریس

ماتریس   معکوس‌پذیر است اگر و تنها اگر .

به ماتریس   رتبه کامل می‌گوییم اگر .

مثال

ماتریس زیر دارای دو ستون (سطر) مستقل خطی است بنابراین رتبه‌ی آن برابر 2 است.

تبدیل خطی

پیشتر درباره‌ی بردارها، و نحوه‌ی جمع کردن دو بردار صحبت کردیم. لازم است اشاره کنیم که اگر بخواهیم یک اسکالر حقیقی مقدار را در یک بردار ضرب کنیم، این ضرب به صورت درایه به درایه انجام می‌شود.

در یک تعریف ساده، بردارها اشیائی هستند که با یکدیگر قابل جمع هستند و اسکالر را می‌توان در آن‌ها ضرب کرد.

اگر تبدیلی روی بردارها اعمال کنیم که دو ویژگی ذکر شده در بالا را حفظ کند، به آن تبدیل خطی می‌گوییم یعنی:

در رابطه‌ی بالا،  و  بردارهای عضو فضای برداری هستند.  و  اسکالرهای حقیقی هستند و ، یک تبدیل خطی است.

به بردارهایی در فضای برداری مقصد، که از فضای برداری مبدا و به کمک تبدیل خطی می‌توان به آن‌ها رسید، تصویر تبدیل خطی می‌گویند.

به بردارهایی در فضای تبدیل خطی مبدا که بردار صفر را در فضای برداری مقصد تولید می‌کنند، هسته تبدیل خطی می‌گویند.

بردار صفر فضای برداری مبدا، همواره عضو هسته‌ی فضای برداری است. در شکل 7 یک شهود هندسی از این مفاهیم نمایش داده شده است.

شکل 7: نمایش هندسی هسته و تصویر تبدیل خطی

دترمینان یک ماتریس

دترمینان از مهم‌ترین مفاهیم موجود در جبر خطی است.

دترمینان یک نگاشت است که فضای ماتریس‌ها را به فضای اعداد حقیقی می‌برد.

یک ماتریس معکوس‌پذیر است اگر و تنها اگر دترمینان آن ناصفر باشد.

همان‌طور که در بخش معکوس‌پذیری ماتریس دیدیم، شرط معکوس‌‌پذیری یک ماتریس دو در دو، است.

در واقع  همان دترمینان ماتریس دو در دو است.

دترمینان ماتریس یک در یک، برابر با تنها درایه‌ی ماتریس است.

دترمینان ماتریس سه در سه به فرم  برابر است با:

به ماتریسی که همه‌ی عناصر بالای قطر اصلی آن صفر باشد، ماتریس پایین مثلثی می‌گوییم. به طور مشابه، به ماتریسی که همه‌ی عناصر پایین قطر اصلی آن صفر باشند، ماتریس بالا مثلثی می‌گوییم.

به عنوان مثال ماتریس  پایین مثلثی است در حالی که ماتریس  بالا مثلثی است.

دترمینان یک ماتریس بالا یا پایین مثلثی به صورت ضرب تمام درایه‌های روی قطر اصلی ماتریس تعریف می‌شود.

دترمینان در واقع حجم فضایی را که بردارهای ستونی ماتریس در فضای برداری می‌سازند را اندازه می‌گیرد.

برخی خواص دترمینان

اضافه کردن مضربی از یک سطر یا ستون به یک سطر یا ستون دیگر، مقدار دترمینان ماتریس را تغییر نمی‌دهد.

اگر یک سطر یا ستون را در یک اسکالر ضرب کنیم، دترمینان نیز در همان اسکالر ضرب می‌شود، به عبارت دیگر:

جابجا کردن دو سطر یا ستون، علامت دترمینان را تغییر می‌دهد.

ماتریس  دارای دترمینان ناصفر است اگر و تنها اگر رتبه‌ی آن برابر با  باشد. به عبارت دیگر، ماتریس معکوس‌پذیر است اگر و تنها اگر رتبه کامل باشد.

تریس یک ماتریس

به مجموع عناصر روی قطر اصلی ماتریس مربعی، تریس ماتریس گفته می‌شود.

برخی خواص تریس ماتریس:

خاصیت آخر قابل تعمیم است یعنی اگر ، ، و  آنگاه داریم:

اگر   و  بردارهایی با بعد  باشند، داریم:

توجه داشته باشید هنگامی که عمل ترانهاده‌ کردن را بر روی یک بردار اعمال می‌کنیم، بردار سطری به ستونی تبدیل می‌شود و برعکس.

چندجمله‌ای مشخصه

به ازای ماتریس  و اسکالر ، چندجمله‌ای مشخصه به صورت زیر تعریف می‌شود:

که در آن

از چندجمله‌ای مشخصه در محاسبه‌ی مقدار و بردار ویژه‌ی ماتریس استفاده می‌شود که در بخش بعدی به آن خواهیم پرداخت.

مقدار و بردار ویژه‌ی یک ماتریس

به ازای ماتریس  و اسکالر  و بردار ، به  مقدار ویژه و به  بردار ویژه می‌گوییم اگر در رابطه‌ی زیر صدق کنند:

معمولا مقادیر ویژه‌ی یک ماتریس را از بزرگ به کوچک مرتب می‌کنند و بین آن‌ها یک ترتیب نزولی قائل می‌شوند. بنابراین منظور از مقدار ویژه‌ی اول، بزرگترین مقدار ویژه است و منظور از بردار ویژه‌ی اول، بردار ویژه‌ی متناظر مقدار ویژه‌ی اول است.

گزاره‌های زیر معادل‌اند:

مقدار ویژه‌ی ماتریس است.

یک بردار وجود دارد که از حل معادله‌ی (یا به طور معادل ( به دست می‌آید.

اگر بردار  بردار ویژه‌ی متناظر با مقدار ویژه‌ی  باشد، هر مضرب غیر از مضرب صفر بردار  نیز یک بردار ویژه‌‌ی متناظر  است.

اسکالر  مقدار ویژه‌ی ماتریس  است اگر و تنها اگر ریشه‌ی چندجمله‌ای مشخصه باشد.

مقادیر ویژه‌ی هر ماتریس با مقادیر ویژه‌ی ترانهاده‌ی ماتریس برابر است اما لزوما بردارهای ویژه‌ی یکسانی ندارند.

مثال

بیایید مقادیر و بردارهای ویژه‌ی ماتریس زیر را بیابیم:

همان‌طور که پیشتر گفتیم، برای یافتن مقادیر ویژه، باید ریشه‌های چندجمله‌ای مشخصه را بیابیم:

در نتیجه ریشه‌ها برابرند با و .

برای یافتن بردارهای ویژه باید معادله‌ی زیر را حل کنیم:

به ازای داریم:

در نتیجه بردار  و تمام بردارهایی که مضرب آن هستند، بردار ویژه‌ی متناظر با مقدار ویژه‌ی 5 هستند.

به ازای ، به طور مشابه داریم:

در نتیجه بردار 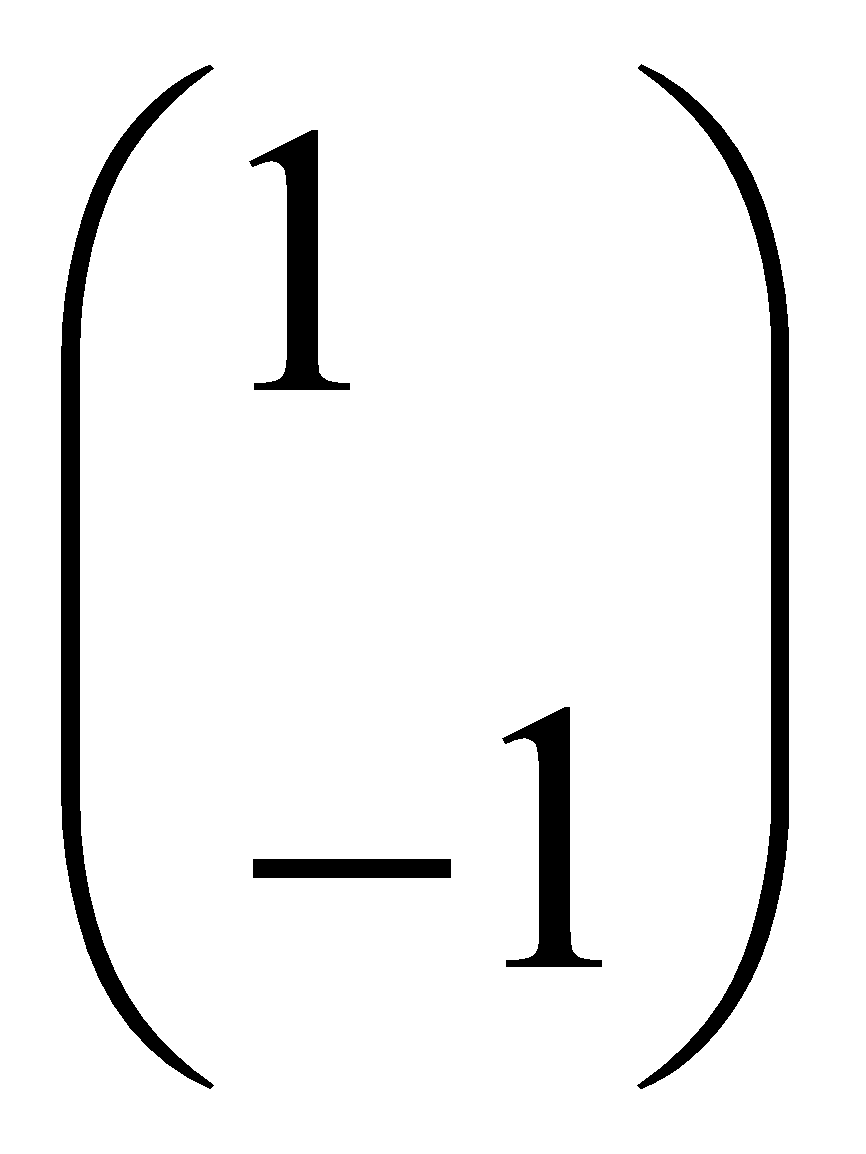 و تمام بردارهای مضرب آن، بردار ویژه‌ی متناظر با مقدار ویژه‌ی 2 هستند.

اگر یک مقدار ویژه به صورت تکراری در ریشه‌های معادله‌ی مربوط به چندجمله‌ای مشخصه ظاهر شود، آنگاه ممکن است به تعداد تکرارها، برای آن مقدار ویژه، بردار ویژه داشته باشیم.

اگر ماتریس دارای مقدار ویژه‌های  باشد، بردار ویژه‌های متناظر آن‌ها مستقل خطی هستند.

دترمینان ماتریس مربعی برابر با حاصل ضرب مقادیر ویژه‌ی آن است.

تریس ماتیس مربعی برابر با حاصل جمع مقادیر ویژه‌ی آن است.

مقدار ویژه و بردار ویژه کاربردهای فراوانی در حل مسائل مختلف دارند. به عنوان در نمونه، گوگل از بردار ویژه‌های متناظر با بزرگترین مقادیر ویژه جهت یافتن مهم‌ترین صفحات وب مرتبط با جستجوی انجام شده استفاده می‌کند.

تجزیه‌ مقادیر منفرد

در برخی مسائل می‌خواهیم ماتریسی که با آن کار می‌کنیم را به چند ماتریس کوچک‌تر تجزیه کنیم. این کار می‌تواند به لحاظ محاسباتی مزایای زیادی داشته باشد.

روش‌های متنوعی برای تجزیه‌ی ماتریس‌ها وجود دارد که یکی از معروف‌ترین‌ و پرکاربردترین‌های آن‌ها، تجزیه مقادیر منفرد است.

یکی از خوبی‌های این روش این است که به وسیله‌ی آن می‌توان هر ماتریسی را تجزیه نمود؛ یعنی محدود به ماتریس‌های مربعی نیستیم.

ایده‌ی کلی این است که یک ماتریس را به صورت حاصل‌ضرب سه ماتریس به فرم زیر بازنویسی کنیم:

اگر ماتریس  باشد، آنگاه ماتریس  ، و ماتریس  است.

ماتریس  هم‌بعد ماتریس  است.

ماتریس  ساختار شبه‌قطری دارد. یعنی اگر مربعی باشد، تنها درایه‌های قطری آن ناصفر هستند. اگر مربعی نباشد، تنها یک شبه‌قطر با شروع از درایه‌ی  تا جایی که ابعاد ماتریس اجازه بدهد، دارای مقادیر ناصفر است.

به مقادیر قطری ماتریس مقادیر منفرد می‌گویند.

در مثال زیر به چگونگی محاسبه‌ی تجزیه مقادیر منفرد ماتریس در پایتون می‌پردازیم.

مثال

ماتریس  را در نظر بگیرید.

در قطعه کد اول تجزیه مقادیر منفرد اجرا شده است و ماتریس‌های  و  نمایش‌داده‌شده‌اند و در قطعه کد دوم ماتریس  را نمایش داده‌ایم.

می‌توانستیم در قطعه کد اول نیز  را چاپ کنیم اما فقط درایه‌های قطری ماتریس  (که ناصفر هستند) را نمایش می‌دهد.

در این مقاله سعی کردیم تا یک مرور کلی بر مفاهیم جبر خطی که در الگوریتم‌های یادگیری ماشین مورد استفاده قرار می‌گیرند داشته باشیم تا بتوانیم در آینده و هنگام مطالعه‌ی مباحث یادگیری ماشین، درک بهتری از این الگوریتم‌ها داشته باشیم.

منابع

https://aman.ai/primers/math/#correlation

Deisenroth, M. P., Faisal, A. A., & Ong, C. S. (2020). Mathematics for machine learning. Cambridge University Press.