مروری بر جبر خطی: اسکلت داده‌ها - قسمت اول

چکیده

جبر خطی شاخه‌ای از ریاضیات است که فضاهای برداری و تبدیل‌های خطی بین فضاهای برداری، مانند چرخاندن یک شکل، بزرگ‌ یا کوچک کردن یک شکل، و یا انتقال آن در فضای برداری را مطالعه می‌کند. یادگیری ماشینی به شدت بر جبر خطی متکی است بنابراین درک بردارها و ماتریس‌ها و اینکه چه عملیات‌هایی را می توانید به کمک آنها در کار با مجموعه داده‌ها انجام دهید، ضروری است. در این پست به طور خلاصه به معرفی مفاهیم مهم و پرکاربرد جبرخطی می‌پردازیم.         

بردارها

تعریف

بردار کمیتی است که با اندازه و جهت تعریف می شود. به عنوان مثال، سرعت یک موشک یک بردار ۳ بعدی است که اندازه ی آن سرعت موشک است و جهت آن، مسیر حرکتش در لحظه است. یک بردار را می توان با آرایه ای از اعداد به نام اسکالر نشان داد. هر اسکالر با توجه با بزرگی بردار در یک بعد (جهت) مطابقت دارد. به عنوان مثال، فرض کنید موشکی با زاویه کمی بالا می رود: سرعت عمودی آن ۵۰۰۰ متر بر ثانیه است و همچنین سرعت ۱۰ متر بر ثانیه به سمت شرق در سرعت ۵۰ متر بر ثانیه به سمت شمال با دارد. سرعت موشک را می توان با بردار زیر نشان داد:

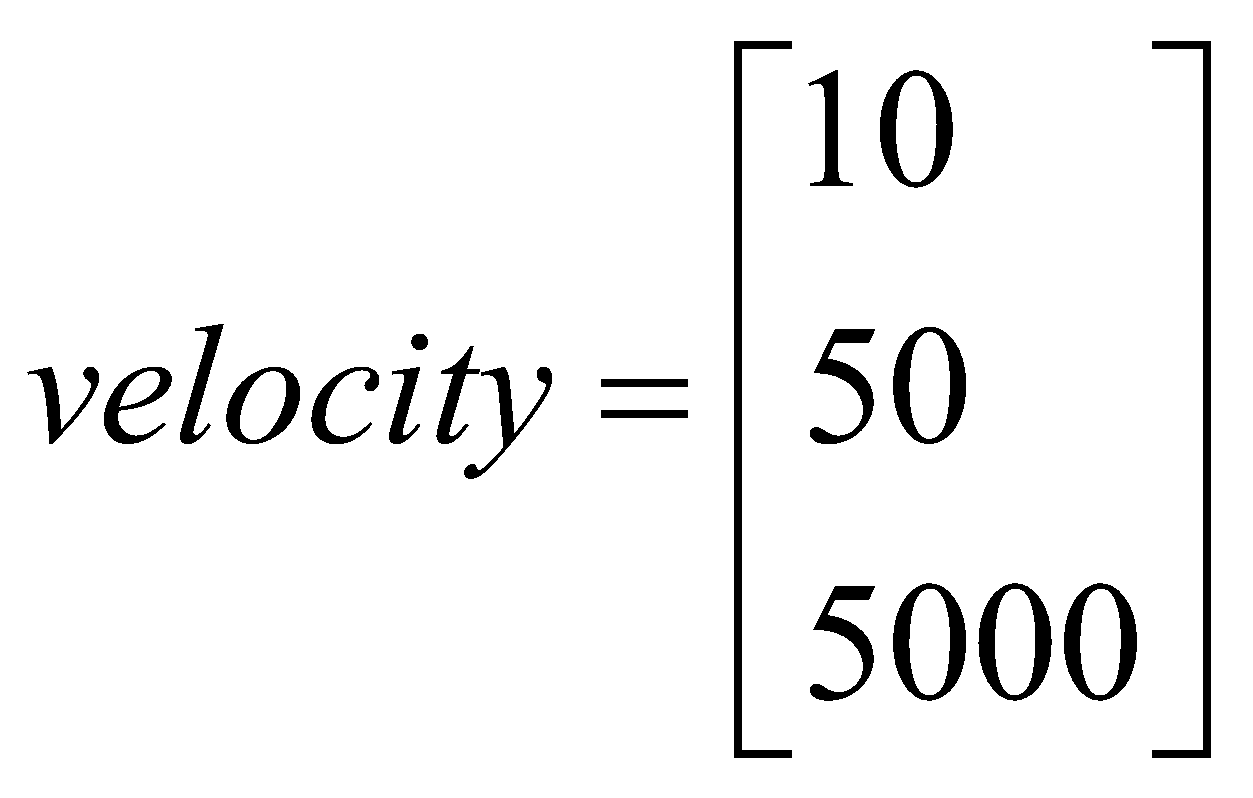
توجه: بر اساس قرارداد، بردارها عموماً به صورت ستونی ارائه می شوند. اسامی بردارها با حروف کوچک انگلیسی نوشته می‌شوند تا از اسامی مربوط به ماتریس‌ها ( که در ادامه به آن‌ها خواهیم پرداخت) قابل تشخیص باشند. همچنین اسامی بردارها در صورت امکان به صورت پررنگ نوشته می‌شود تا از مقادیر اسکالر ساده مانند ۵۰۰۰ متر بر ثانیه قابل تفکیک باشند.

لیستی از N عدد نیز ممکن است مختصات یک نقطه را در فضای N بعدی نشان دهد، بنابراین بسیار پیش می‌آید که بردارها را در نمایش هندسی به‌جای فلش‌ به صورت نقاط ساده نشان دهیم. یک بردار با ۱ عنصر ممکن است به عنوان یک فلش یا یک نقطه روی یک محور، یک بردار با ۲ عنصر یک فلش یا یک نقطه در یک صفحه، یک بردار با ۳ عنصر یک فلش یا یک نقطه در فضا و یک بردار با عناصر N یک فلش یا یک نقطه در یک فضای N-بعدی است که تصور آن برای اکثر مردم سخت است. در شکل 1 یک بردار دو بعدی با طول 1 و عرض 2 را در محور مختصات دکارتی مشاهده می‌کنید.

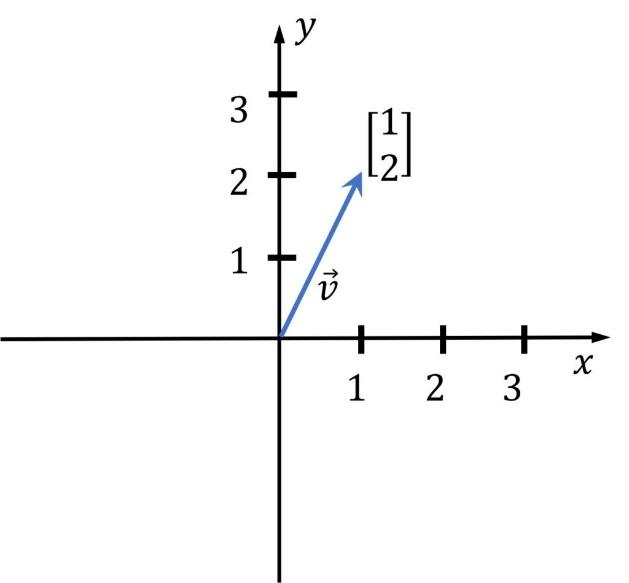
شکل 1: نمایش گرافیکی یک بردار دوبعدی

هدف

بردارها با اهداف زیادی در یادگیری ماشین استفاده می‌شوند، به ویژه برای نمایش مشاهدات و پیش‌بینی‌ها. به عنوان مثال، فرض کنید ما یک سیستم یادگیری ماشینی ساخته‌ایم تا ویدیوها را بر اساس اطلاعاتی که در مورد آنها می‌دانیم به ۳ دسته (خوب، هرزنامه، طعمه کلیک) دسته‌بندی کنیم. بنابراین برای هر ویدیو، یک بردار خواهیم داشت که نشان دهنده دانسته‌های ما در مورد آن است، مانند:

بردار بالا می تواند ویدیویی را نشان دهد که مدت زمانش ۱۰.۵ دقیقه است، اما تنها ۵.۲ درصد بینندگان برای بیش از یک دقیقه آن را تماشا می کنند، به طور متوسط ۳.۲۵ بازدید در روز دریافت می کند و ۷ بار به عنوان هرزنامه (spam)  نشان‌ گذاری شده‌است. همانطور که می بینید، هر بعد ممکن است معنای متفاوتی داشته باشد.

بر اساس بردار بالا، سیستم یادگیری ماشین ما ممکن است پیش‌بینی کند که با احتمال ۸۰ درصد این ویدئو یک ویدیوی هرزنامه است، ۱۸ درصد یک ویدیوی طعمه‌ی کلیکی و ۲ درصد یک ویدیوی خوب است. این خروجی می‌تواند به صورت بردار زیر نمایش داده شود:

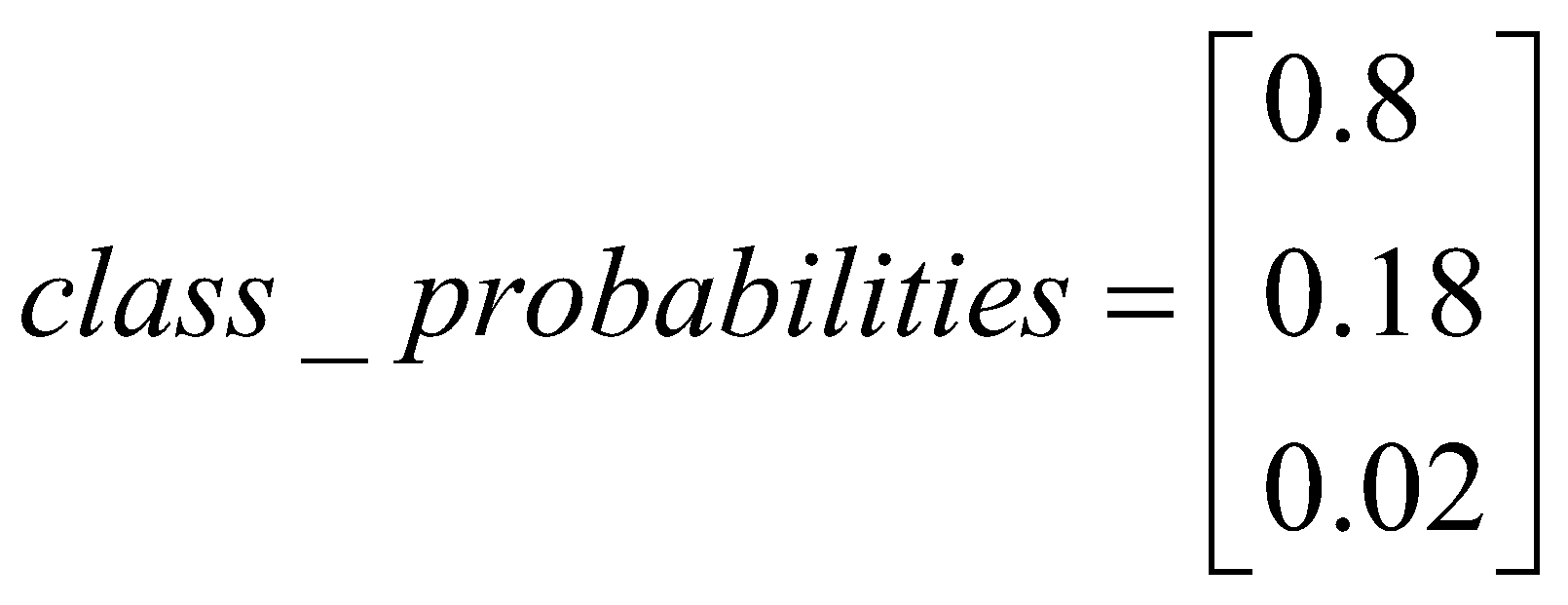
بردارها در پایتون

در پایتون، یک بردار را می توان به روش های مختلفی نشان داد، ساده‌ترین آنها لیست معمولی اعداد در پایتون است:

از آنجایی که ما قصد داریم محاسبات علمی بسیار زیادی انجام دهیم، بهتر است از  NumPy ndarray   استفاده کنیم که بسیاری از پیاده سازی‌های راحت و بهینه مربوط به عملیات‌های ریاضی ضروری برای کارها با بردارها را ارائه می دهد مثلا:

اندازه (تعداد ابعاد) یک بردار را می توان با استفاده از متد attribute بدست آورد:

عنصر iام بردار v با vi مشخص می‌شود.

توجه داشته باشید که اندیس‌ها در ریاضیات معمولاً از ۱ شروع می شوند، اما در برنامه نویسی معمولاً از ۰ شروع می شوند. بنابراین برای دسترسی به عنصر سوم بردار video می‌نویسیم:

ترسیم بردارها

برای رسم بردارها، از کتابخانه‌ی matplotlib استفاده می کنیم، پس بیایید با ایمپورت کردن آن شروع کنیم.

در یک نوت بوک Jupyter/Colab، ما به سادگی می توانیم نمودارهای خود را درون نوت بوک و با اجرای دستور زیر خروجی بگیریم.

بردارهای دوبعدی

اکنون، کتابخانه‌ی NumPy را برای مدیریت آرایه‌ها وارد کنید تا بردارهای ورودی را که می‌خواهیم ترسیم کنیم، مدیریت کنیم:

بیایید چند بردار دو بعدی ساده برای ترسیم ایجاد کنیم:

این بردارها هر کدام دارای ۲ عنصر هستند، بنابراین به راحتی می توان آنها را به صورت گرافیکی بر روی یک صفحه‌ی دو بعدی، به عنوان مثال در شکل 2 به صورت نقطه نشان داده می‌شود:

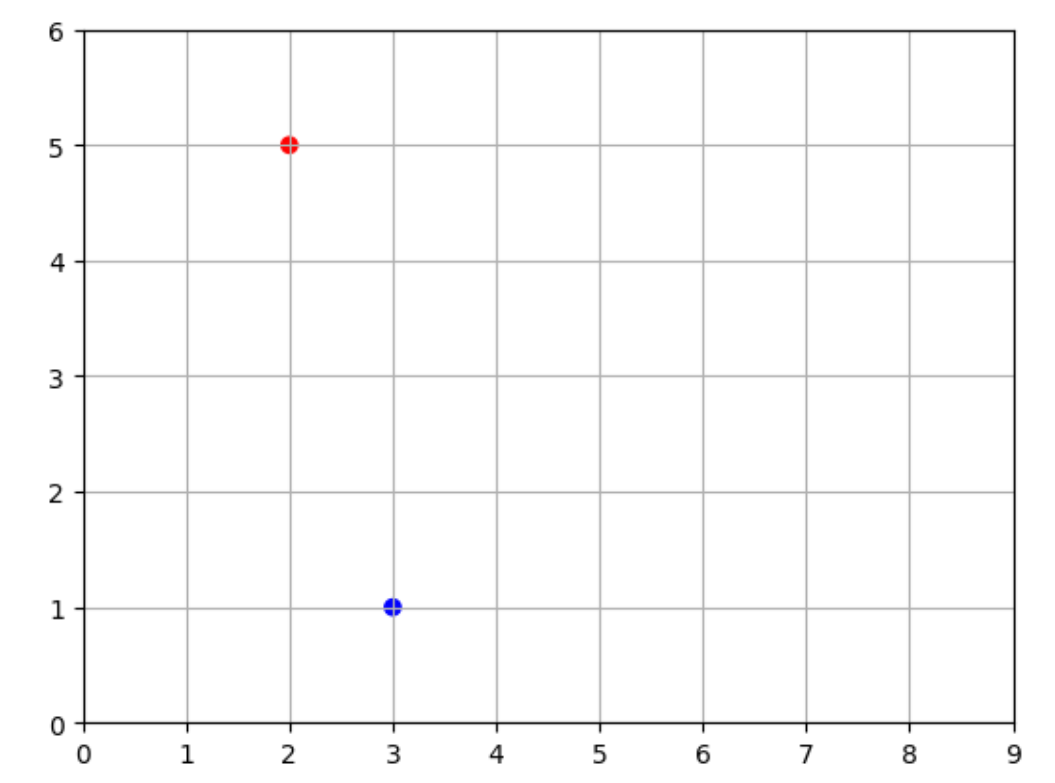
شکل 2: نمایش دو بردار دو بعدی در یک صفحه‌ی دوبعدی

بردارهای سه‌بعدی

ترسیم بردارهای سه‌بعدی نیز نسبتاً ساده است. ابتدا دو بردار سه‌بعدی ایجاد می‌کنیم:

حالا بیایید این بردارها را با استفاده ازAxes3D در کتابخانه‌ی  matplotlibترسیم کنیم. توجه داشته باشید که ما از mpl_toolkits برای انجام این مرحله استفاده خواهیم کرد (و کتابخانه‌ی matplotlib، mpl_toolkits را به عنوان یک مجموعه کد وابسته، در حین نصب، بارگیری نمی کند). بنابراین بیایید ابتدا آن را با استفاده از

 pip install --upgrade matplotlib

بارگیری کنیم (اگر این کد را در نوت بوک Jupyter اجرا می کنید، از

 !pip install --upgrade matplotlib

استفاده کنید. در شکل 3 دو بردار سه‌بعدی را در فضای سه‌بعدی مشاهده می‌کنید.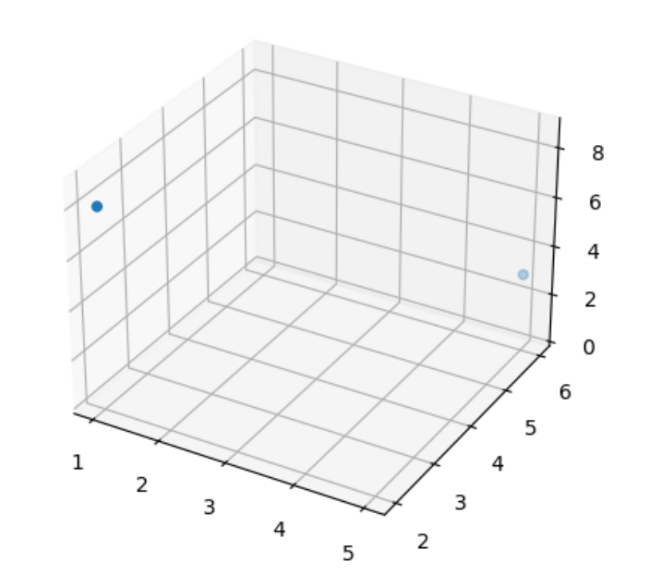

شکل 3: نمایش دو بردار سه‌بعدی در یک صفحه‌ی سه بعدی

تجسم اینکه این دو نقطه دقیقاً کجای فضا هستند کمی سخت است، بنابراین بیایید خطوط عمودی را به نمودار اضافه کنیم. در شکل 4 محل بردارهای سه بعدی را با خطوط عمودی مشخص می‌کنیم:

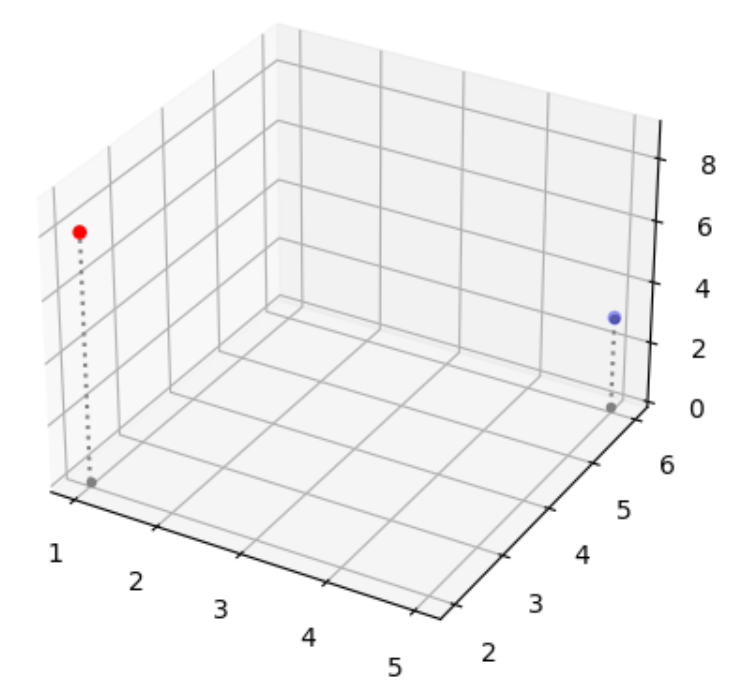
شکل 4: نمایش دو بردار سه‌بعدی در یک فضای سه‎بعدی

نُرم (اندازه‌) بردار

نرم بردار u که به ∣∣ ∣∣uنشان داده می‌شود، اندازه‌گیری طول (اندازه) بردار u است. نرم‌های متعددی وجود دارد، اما رایج ترین نرم (و تنها موردی که در اینجا به آن خواهیم پرداخت) نرم اقلیدسی است که به صورت زیر تعریف می شود:

با یادآوری رابطه‌ی  می‌توانیم به راحتی نرم اقلیدسی را در پایتون پیاده‌سازی کنیم:

با این حال، استفاده از تابع نرم کتابخانه‌ی NumPy که در ماژول linalg (جبر خطی) موجود است بسیار کارآمدتر است:

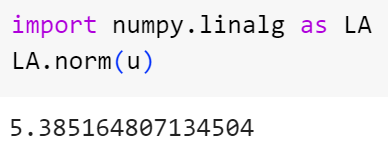
بیایید یک نمودار ساده رسم کنیم تا به صورت هندسی نشان دهیم که طول بردار v واقعاً حدود ۵.۴ است:

شکل 4: نمایش هندسی نرم یک بردار

درست به نظر می رسد!

محاسبات برداری

بردارهای هم‌اندازه را می توان با هم جمع کرد. جمع به صورت عنصر به عنصر انجام می‌شود:

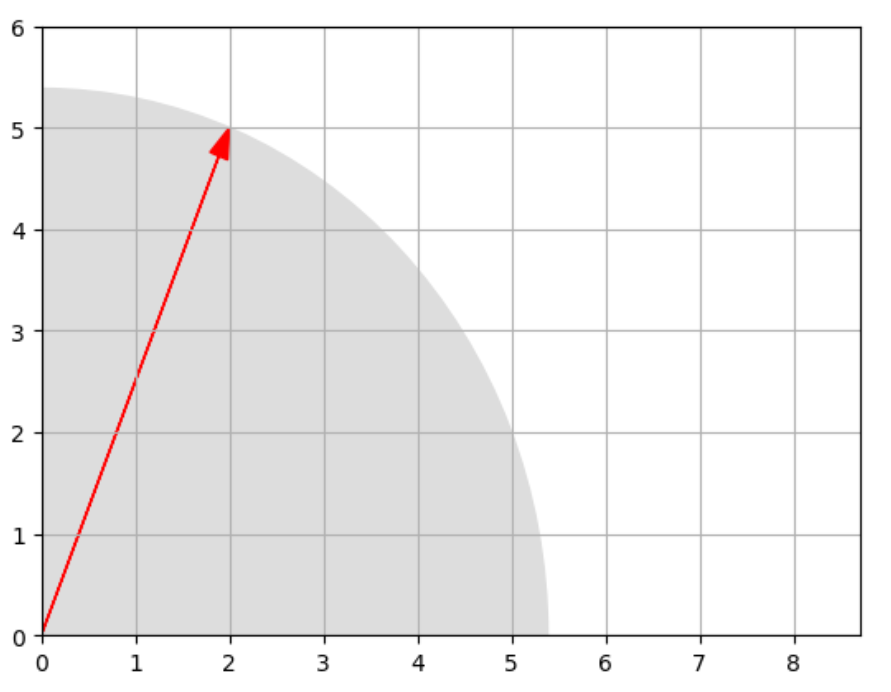
بیایید ببینیم که جمع برداری از نظر هندسی چگونه به نظر می‌رسد:

شکل 5: نمایش هندسی جمع برداری

جمع برداری، جابجایی‌پذیر است، یعنی :

می‌توانید این مفهوم را در شکل 5 مشاهده کنید: دنبال کردن u و سپس بردار v به همان نقطه ای منجر می‌شود که انگار ابتدا v و سپس u دنبال شدند.

جمع برداری شرکت‌پذیر نیز است، به این معنی که:

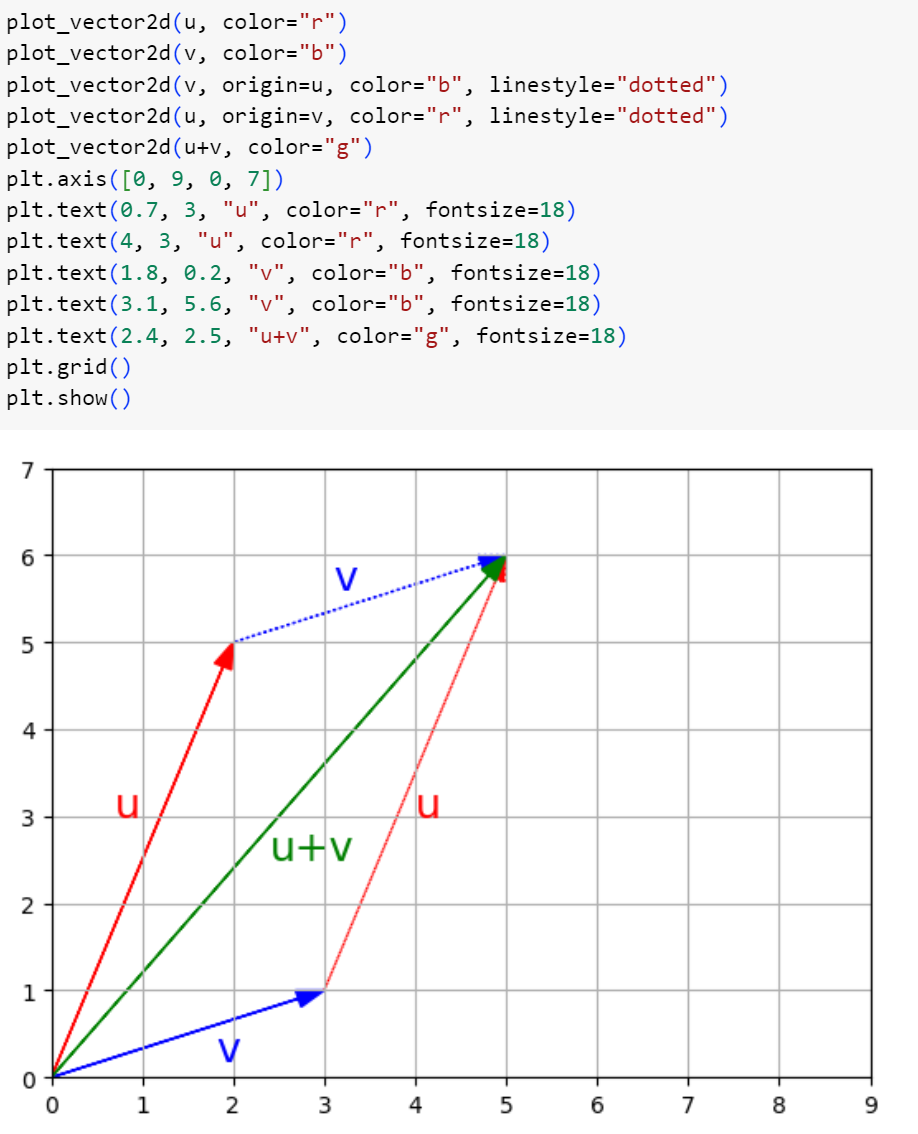
اگر شکلی داشته باشید که با تعدادی نقطه (بردار) تعریف شده باشد، و بردار دلخواه v را به همه‌ی این نقاط اضافه کنید، کل شکل به اندازه‌ی v جابجا می‌شود. این جابجایی، انتقال هندسی نامیده می‌شودکه در کد زیر مشاهده می‌شود:

شکل 6: نمایش هندسی انتقال برداری

آخرین نکته در اینجا این است که تفریق یک بردار مانند اضافه کردن همان بردار با علامت مخالف است. ادامه‌ی جبر خطی را در قسمت بعدی توضیح میدهیم.