پلی میان مدلهای رگرسیونی ساده و پیچیده
ترجمه مهدی نورایی از مقاله a bridge between simple and complex regression models

مقدمه
در مقالهی رگرسیون خطی و رگرسیون لاسو و ریج، به مدلهایی پرداختیم که اساساً به دنبال کشف یک رابطهی خطی بین متغیرهای مستقل و وابسته هستند. اما در مسائل واقعی خیلی مواقع پیش میآید که بین متغیرهای مستقل و وابسته یک رابطهی خطی برقرار نباشد. در این مقاله میخواهیم به همین موضوع بپردازیم و ببینیم در چنین مواقعی بهتر است چهکار کنیم.
رابطهی غیرخطی و رگرسیون ذاتاً خطی
گفتیم که یکی از سادهترین روشها برای تشخیص نوع ارتباط دو متغیر، رسم نمودار پراکندگی آن متغیرها در مقابل یکدیگر است. خیلی مواقع با رسم نمودار پراکندگی (پراکنش) بین متغیرها میتوانیم ببینیم که با افزایش یا کاهش مقدار یک متغیر، متغیر مقابل چه رفتاری از خود نشان میدهد.
فرض کنید در یک موقعیت واقعی و هنگامی که مجموعهدادهٔ واقعی کار میکنید، نمودار پراکندگی بین متغیرها را رسم کردید و یک رابطهی غیرخطی بین آنها مشاهده کردید. بهتر است در این موقعیت، امیدتان را به مدلهایی که تا الان یاد گرفتهاید از دست ندهید؛ زیرا همچنان ممکن است آنها بتوانند به کارتان بیایند.
اگر با چنین موقعیتی مواجه شدید، بهتر است اولین اقدامتان این باشد که ارتباط متغیر پاسخ را با فرمهای تابعی شناختهشدهی دیگری از متغیر مستقل بسنجید.
بهعنوانمثال میتوانید نمودار پراکندگی متغیر پاسخ را در برابر توان دوم یا توانهای بالاتر، لگاریتم، فرم نمایی، جذر و... متغیر مستقل رسم کرد.
اگر در هر کدام از این نمودارها یک رابطهی خطی کشف کردید، به شما تبریک میگوییم؛ زیرا هنوز میتوانید از مدلهایی که تا الان آموختهاید استفاده کنید.
کافی است هنگام ورودی دادن به مدل، بهجای اینکه از فرم خام متغیر مستقل استفاده کنید، از فرم تابعی آن استفاده کنید. بهعنوانمثال اگر بین متغیر پاسخ و توان سوم متغیر مستقل یک ارتباط خطی وجود دارد، توان سوم متغیر مستقل را بهعنوان متغیر مستقل مدل در نظر بگیرید و از فرم خام آن صرفنظر کنید.
بهاینترتیب شما دوباره به فضای خطی برمیگردید و میتوانید از مزایای آن بهرهمند شوید. همچنین میتوانید اینگونه تبدیلات را بر روی متغیر پاسخ نیز اعمال کنید.
توجه داشته باشید که اگر به کمک هر تبدیلی بتوان چنین رابطهی خطیای را بین دو متغیر کشف کرد، میگوییم که جنس رابطهی بین دو متغیر ذاتاً خطی است. اما اگر هیچ تبدیلی را پیدا نکنیم که ما را به یک رابطهی خطی برساند، میگوییم که رابطهی بین دو متغیر غیرخطی است. تا زمانی که رابطهی بین دو متغیر ذاتاً خطی است، میتوان از مدلهای رگرسیونی خطی بهره برد.
بعد از اتمام فرایند آموزش و آزمون مدل، وقتی به مرحلهی کاربرد عملی مدل میرسیم، متغیرهای مورد تبدیل قرار گرفته را به مدل میدهیم و اگر مدل روی متغیر پاسخ تبدیل یافته آموزشدیده است، پیشبینیهای مدل را با اعمال معکوس تبدیل به فضای مقادیر واقعی برمیگردانیم تا بتوانیم از آنها استفاده کنیم.
تبدیل باکس - کاکس
اگر هیچکدام از فرمهای تابعی که به ذهنتان میرسد کمکی به کشف یک رابطهی خطی نکرد و همچنان شاهد روابط غیرخطی بودید، بهعنوان تیر آخر تبدیل توانی باکس - کاکس را معرفی میکنیم.
تبدیل باکس - کاکس یک تبدیل توانی قوی است که به مقاصد مختلف مورداستفاده قرار میگیرد. اگر رابطهی بین دو متغیر خطی نباشد، اگر دادههایتان از توزیع نرمال پیروی نکنند و اگر واریانس متغیر موردنظرتان همگن (ثابت) نباشد، میتوانید از تبدیل باکس - کاکس کمک بگیرید.
فرمول این تبدیل را در اینجا ذکر میکنیم؛ اما لازم نیست که شما از این فرمول در پروژههایتان استفاده کنید؛ زیرا این تبدیل بهصورت آماده در کتابخانههای پایتون پیادهسازی شده است و میتوانید از آنها استفاده کنید.
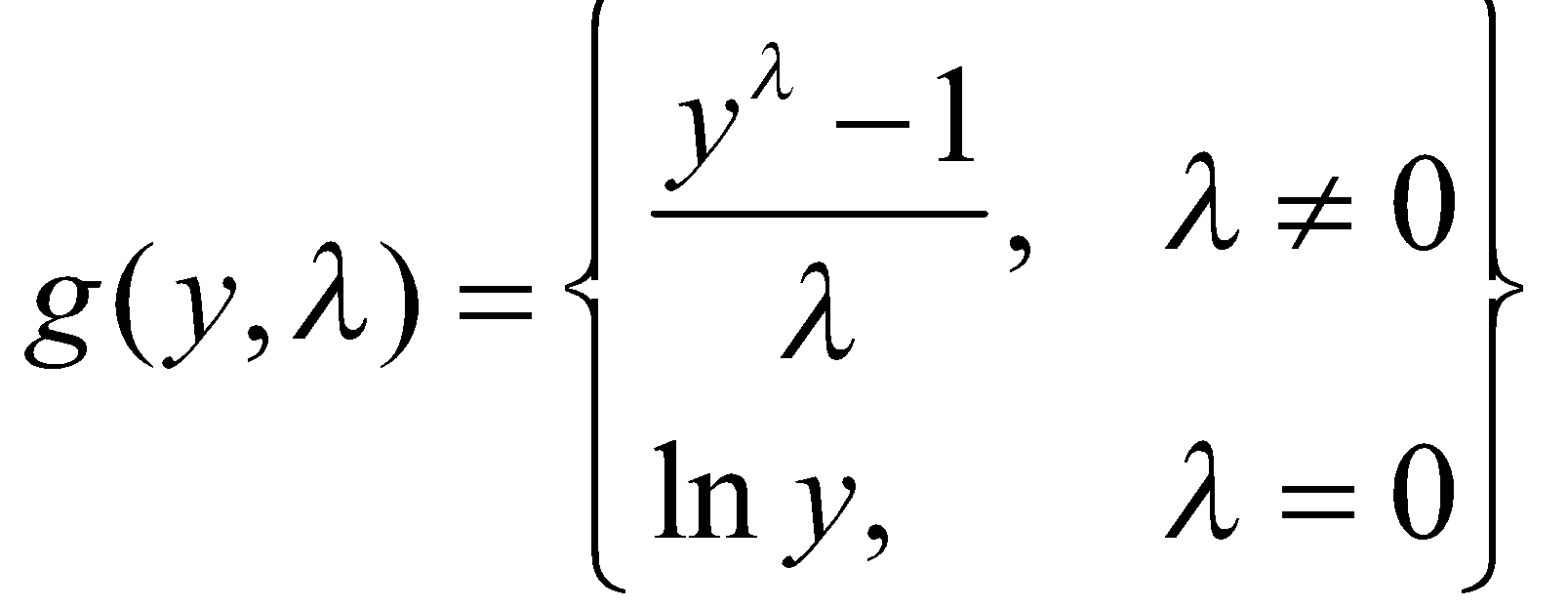
همانطور که در رابطهی بالا مشاهده میکنید، یک پارامتر در این تبدیل وجود دارد که آن را با ![]() نمایش میدهیم. پارامتر
نمایش میدهیم. پارامتر ![]() از یک فرایند بهینهسازی تقریباً مشابه آنچه که در تخمین پارامترهای مدل رگرسیونی به کار بردیم به دست میآید.
از یک فرایند بهینهسازی تقریباً مشابه آنچه که در تخمین پارامترهای مدل رگرسیونی به کار بردیم به دست میآید.
براساس مقدار تخمینزدهشده برای پارامتر ![]() و با کمک رابطهی بالا تصمیم میگیریم که چگونه تبدیل را بر روی متغیر مورد نظر اعمال کنیم.
و با کمک رابطهی بالا تصمیم میگیریم که چگونه تبدیل را بر روی متغیر مورد نظر اعمال کنیم.
توجه داشته باشید که تبدیل باکس - کاکس را فقط روی دادههای مثبت میشود اعمال کرد؛ بنابراین اگر دادههایتان حاوی مقادیر 0 یا منفی بود، قبل از اعمال تبدیل باکس-کاکس باید با یک تبدیل مناسب دادههایتان را مثبت کنید.
یک نکتهی دیگر که باید به آن توجه داشته باشیم نیز این است که استفاده از تبدیل باکس - کاکس معجزه نمیکند. منظورمان این است که این تبدیل نیز گاهی میتواند مفید باشد و گاهی از پس خطی کردن برخی دادهها برنمیآید.
در ادامه با چند مثال کوتاه عملی سعی میکنیم تا مطالبی که تا اینجا بیان کردیم را بهصورت عملی نشان دهیم.
مثال عملی
ابتدا ۱۰۰ نقطه را در فاصلهی ۱ تا ۱۰ در نظر میگیریم و این متغیر را بهعنوان متغیر مستقل در نظر میگیریم. متغیر پاسخ را برابر با مجذور متغیر مستقل در نظر میگیریم. در مثالهای بعدی این رابطه را پیچیدهتر خواهیم کرد.
با رسم نمودار پراکندگی این دو متغیر مشاهده میکنیم که همانطور که انتظار داشتیم، یک رابطهی دقیق از جنس چندجملهای درجهی دوم بین این دو متغیر حاکم است.
از آنجا که ما این فرم تابعی را میشناسیم، بهمحض دیدن چنین رابطهای در مجموعهدادهمان، میتوانیم به سراغ تبدیلی برویم که این رابطه را برایمان به یک رابطهی خطی تبدیل کند.
میدانیم که معکوس تبدیل توان دوم، ریشهی دوم است؛ بنابراین کافی است تا از متغیر پاسخ جذر بگیریم تا شاهد یک رابطهی خطی باشیم.
اگر چه ما متغیرها را خودمان ساختیم؛ اما شما ممکن است در کار با مجموعهدادههای واقعی بهمراتب به موقعیتهای مشابه برخورد کنید.
بهطورکلی هرگاه در نمودار پراکنش بین متغیر مستقل و پاسخ رابطهای را مشاهده کردید که فرم تابعی آن برایتان آشنا و شناختهشده بود، تلاش کنید تا با اعمال عکس آن فرم، رابطه را خطی کنید.

شکل1: ایجاد یک مجموعه داده را با رابطهی درجه دوم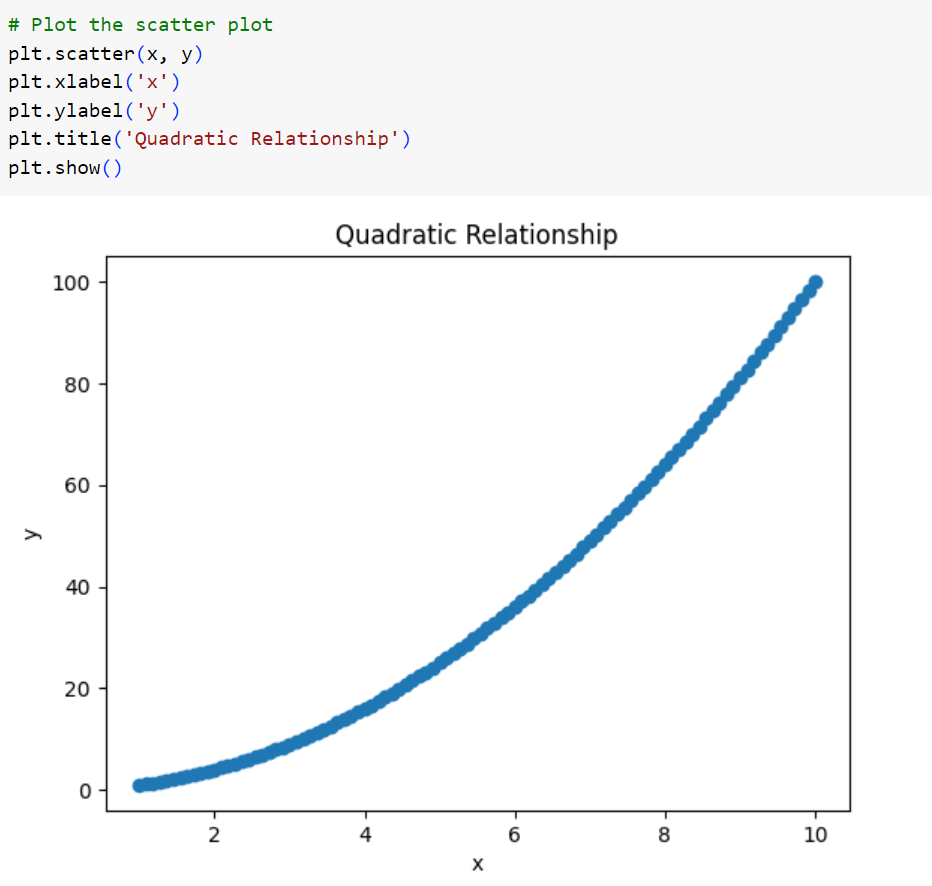
شکل 2: ترسیم مجموعه دادهی ایجادشده با رابطهی درجه دوم
همانطور که در شکل پایین میبینید، پس از جذرگیری از متغیر پاسخ، به یک رابطهی خطی دقیق رسیدیم.
باز هم تأکید میکنیم که اگر با اعمال یک تبدیل به فرم خطی رسیدید، توجه داشته باشید که در فرایند آموزش و آزمون مدل باید از متغیر تبدیل یافته استفاده کنید و هنگامی که مدل برای شما پیشبینی انجام میدهد، با اعمال عکس تبدیل، پیشبینیها را به فضای مقادیر واقعی متغیر منتقل کنید.
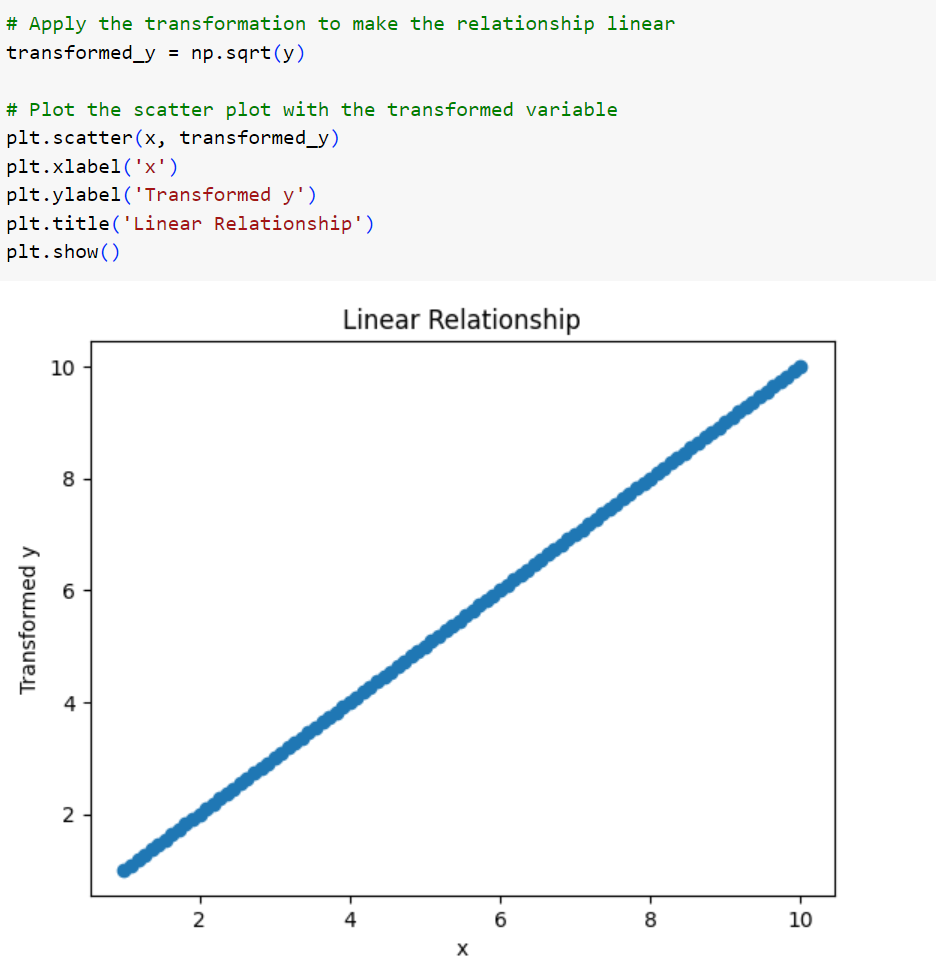
شکل 3: نمودار ارتباط متغیرها پس از جذرگیری
حال بیایید تا مثال را کمی پیچیدهتر کنیم. این بار در فاصلهی 5 تا 20، 100 نقطه را بهعنوان متغیر مستقل در نظر میگیریم. این بار متغیر پاسخ علاوه بر اینکه یک رابطهٔ توان دومی با متغیر مستقل دارد، دارای نویزی از جنس توزیع نرمال با میانگین 0 و انحراف معیار 2 است. 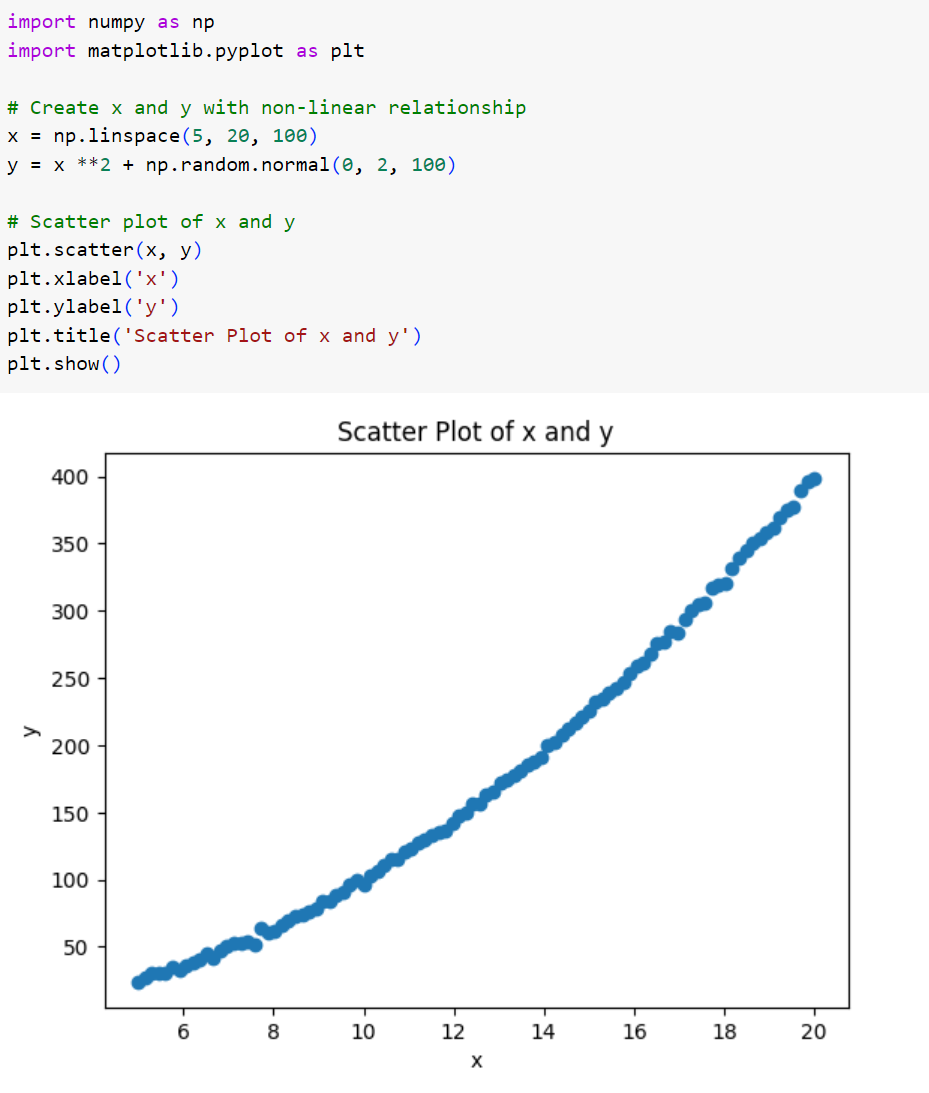
شکل 4: ایجاد و ترسیم مجموعه داده با رابطهی درجه دوم و نویز
بیایید این بار از تبدیل باکس - کاکس استفاده کنیم و ببینیم نتیجه چگونه خواهد بود.
توجه داشته باشید که تبدیل را هم روی متغیر مستقل و هم روی متغیر وابسته اعمال میکنیم.
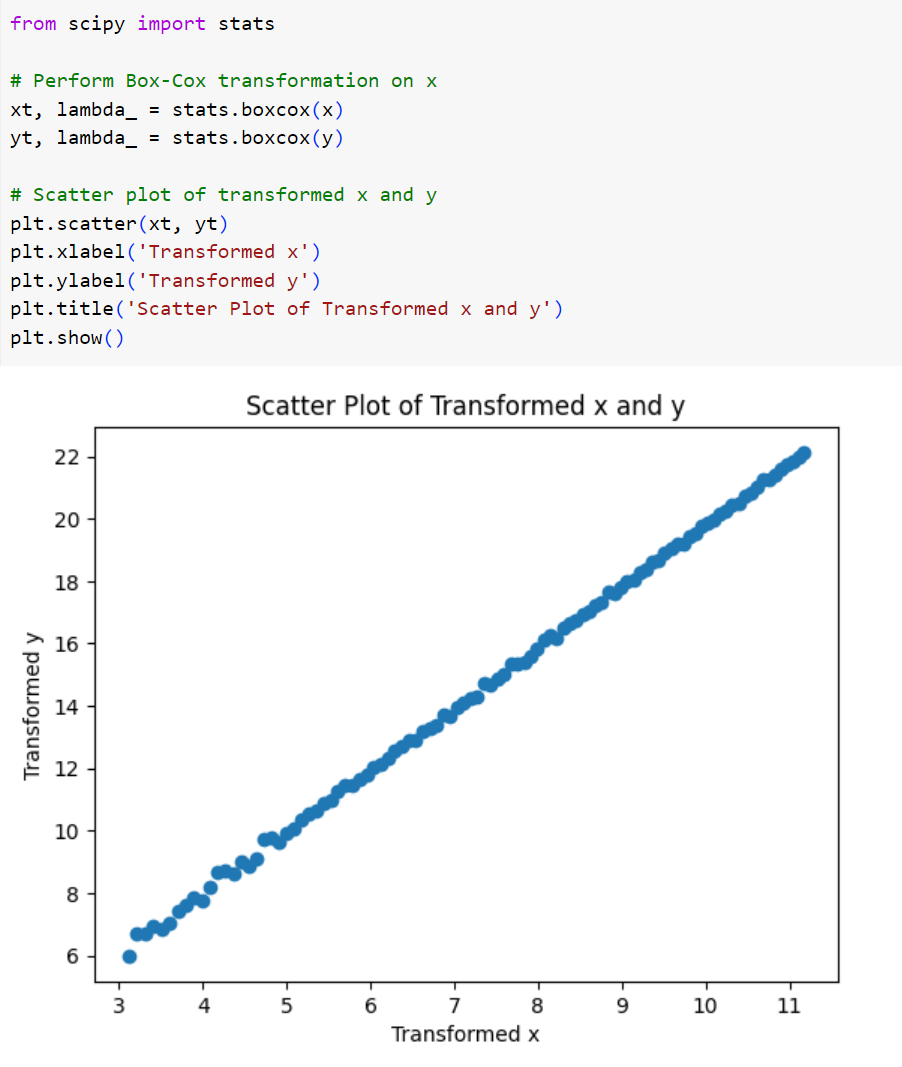
شکل 5: نمودار متغیرهای مجموعه داده پس از اعمال تبدیل باکس-کاکس
همان گونه که در شکل بالا میبینید، تبدیل باکس - کاکس بهخوبی این رابطه را خطی کرده است.
حال بیایید مثالمان را کمی سختتر بکنیم. این بار رابطه را از جنس درجه پنجم در نظر میگیریم. ازآنجاکه توان پنجم متغیر مستقل اعداد بسیار بزرگی خواهند بود، انحراف معیار توزیع نرمالی را که برای تولید نویز استفاده میکنیم را برابر با یک عدد بسیار بزرگ قرار میدهیم.
در شکل زیر فرم رابطه را مشاهده میکنید:
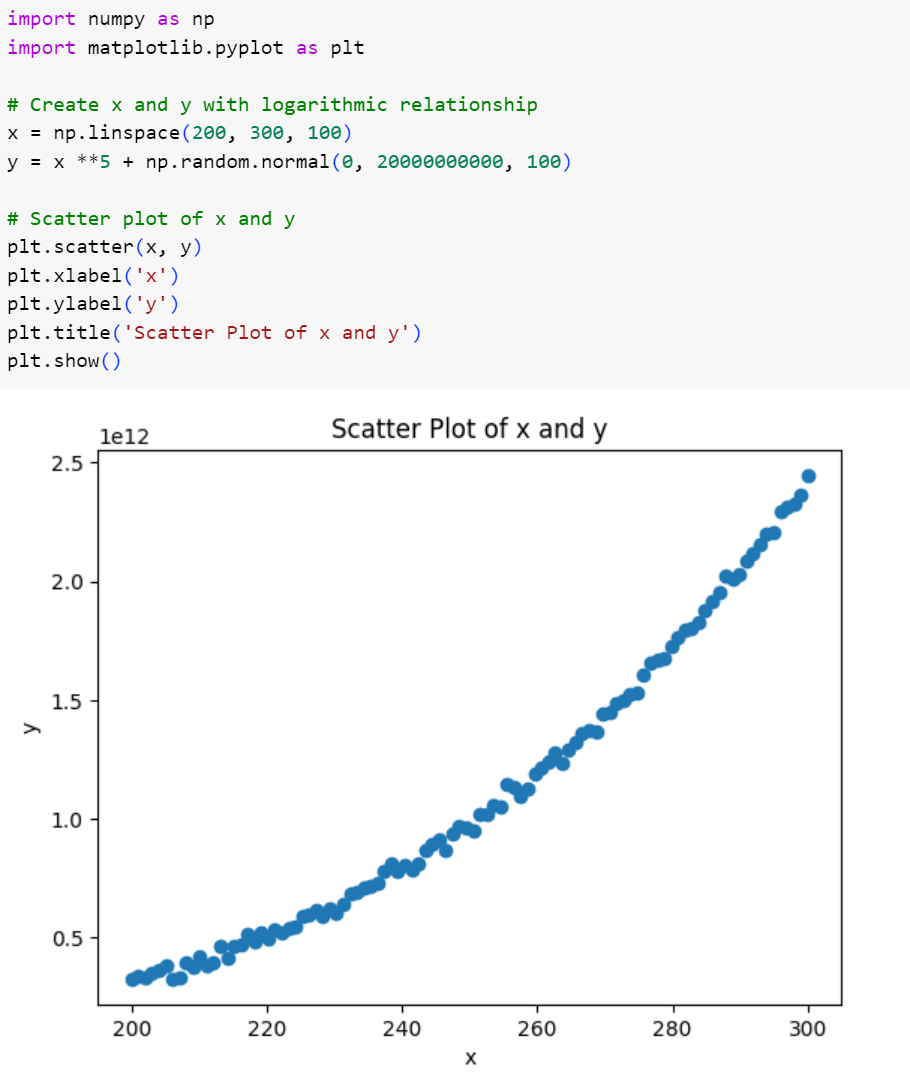
شکل 6: ایجاد و ترسیم نمودار مجموعه دادهی درجه پنجم و با نویز شدید
حال بیایید تا ببینیم تبدیل باکس - کاکس چه عملکردی بر روی این رابطه دارد.
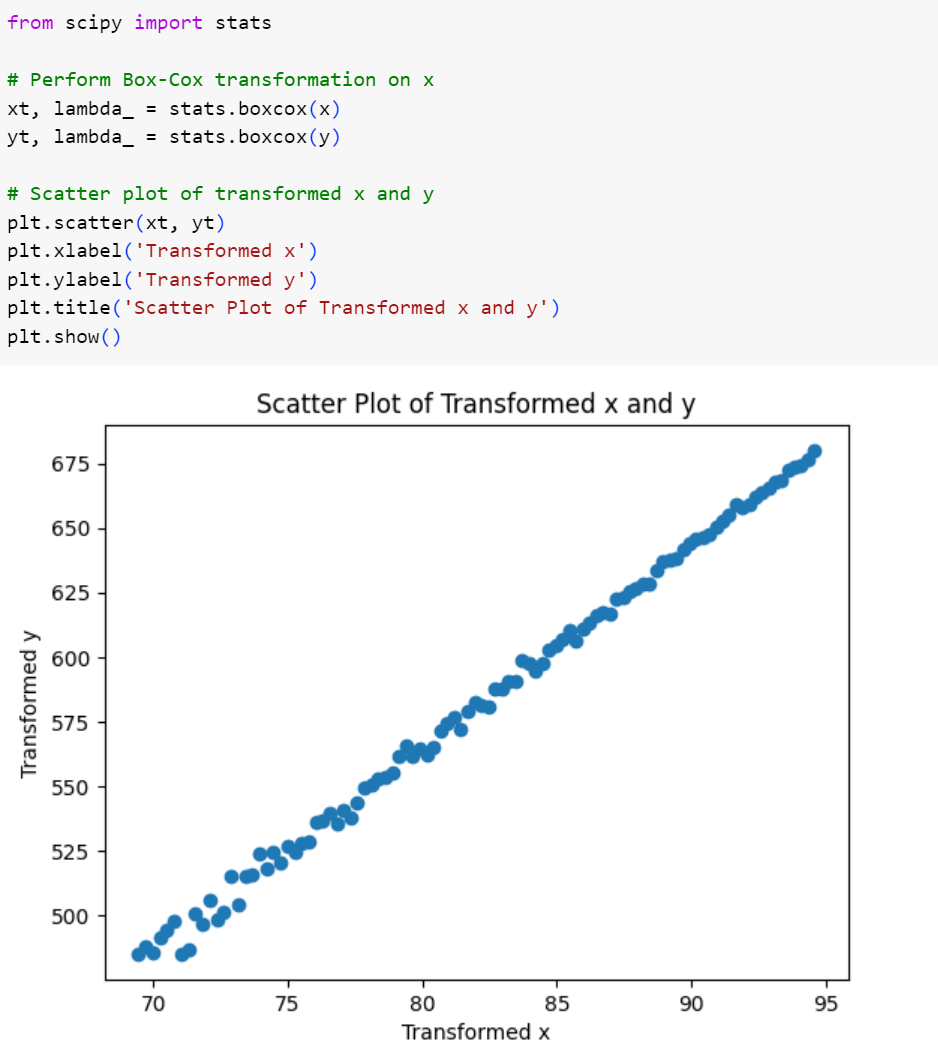
شکل 7: نمودار متغیرهای مجموعه داده پس از اعمال تبدیل باکس-کاکس
همانطور که در شکل بالا میبینیم، باز هم تبدیل باکس- کاکس در خطیسازی رابطهی بین دو متغیر بسیار خوب عمل کرده است.
حال میخواهیم یکی از موقعیتهایی را به شما نشان دهیم که تبدیل باکس -کاکس عملکرد خوبی در آن ندارد.
بیایید این بار رابطهی بین دو متغیر را بهصورت لگاریتمی در نظر بگیریم:
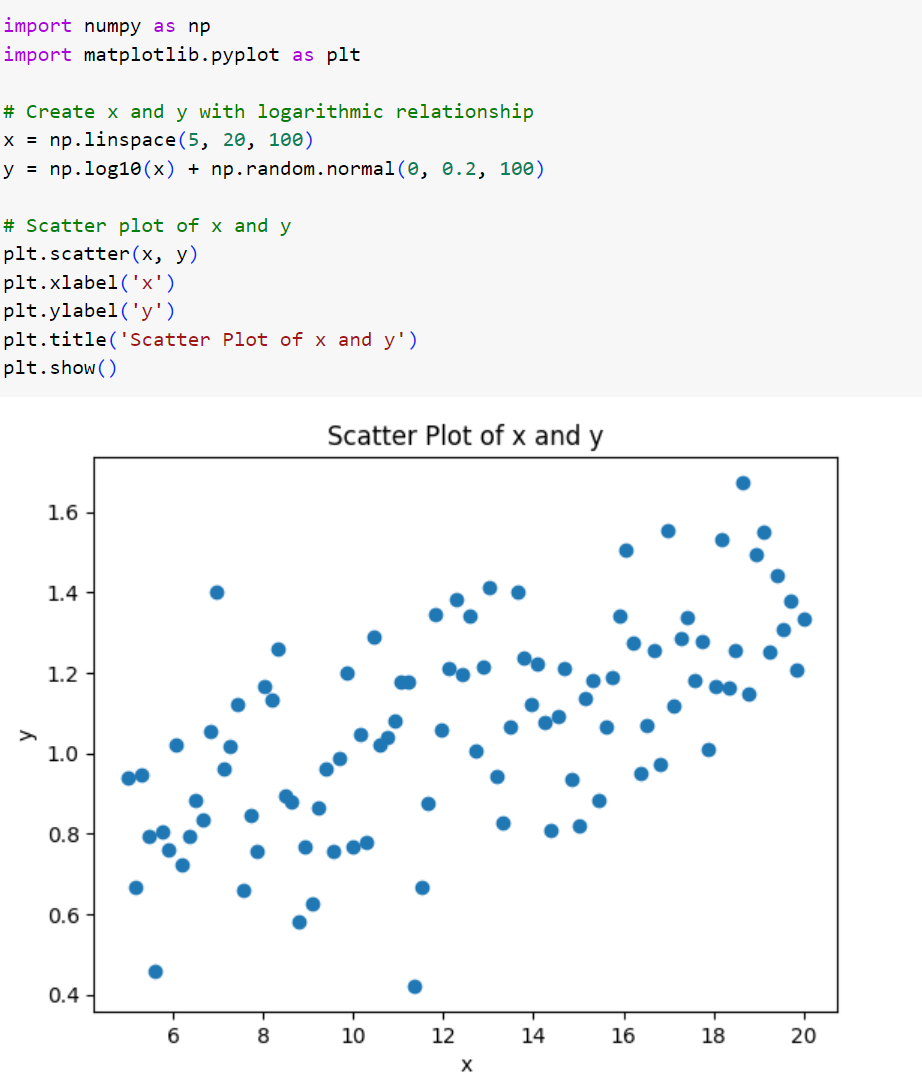
شکل 8: ایجاد و ترسیم نمودار مجموعه دادهی لگاریتمی به همراه نویز
حال بیایید تا عملکرد تبدیل باکس - کاکس را روی این داده بررسی کنیم.
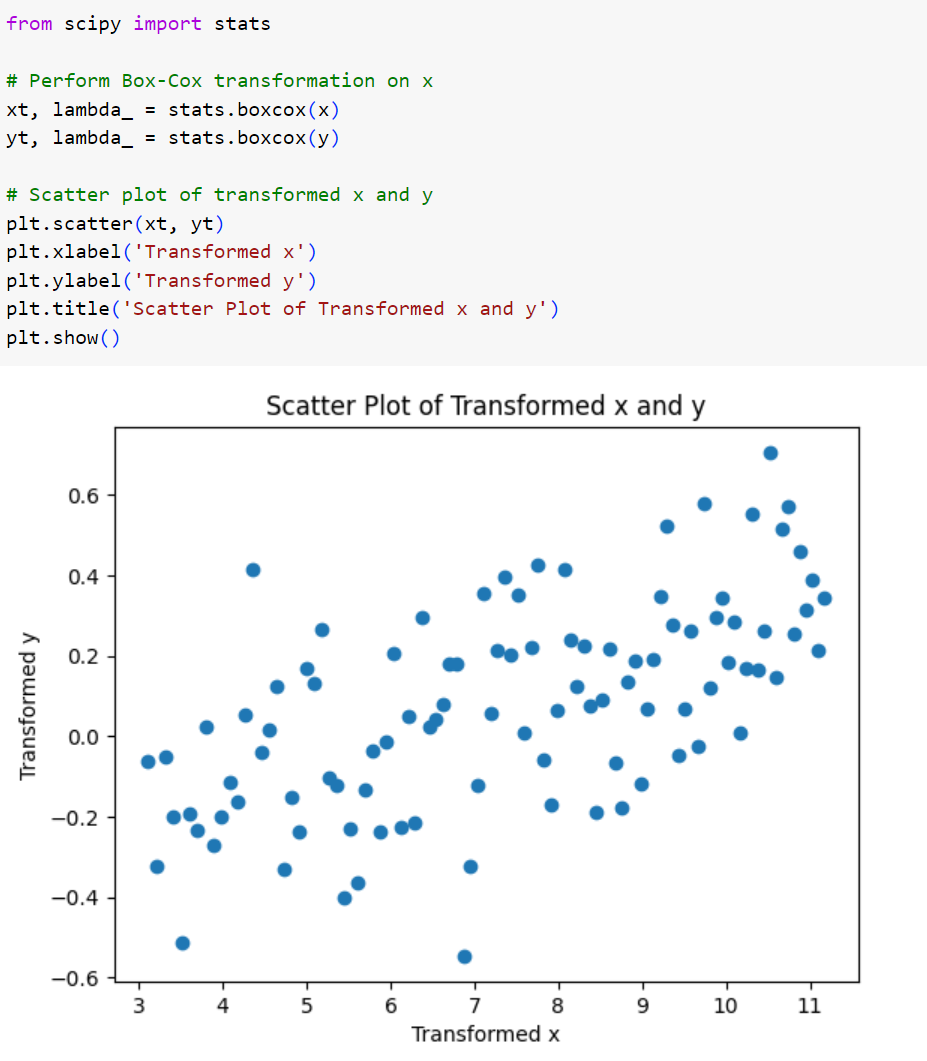
شکل 9: نمودار پراکندگی دو متغیر پس از اعمال تبدیل باکس-کاکس
همانطور که ملاحظه میکنید، تبدیل باکس - کاکس عملاً کار خاصی انجام نداده است و نتوانسته است پراکندگی نقاط را در یک رابطهی خطی خلاصه کند.
البته در این مثال خاص ازآنجاکه میدانیم یک رابطهی لگاریتمی بین دو متغیر حاکم است، میتوانیم با اعمال عکس تبدیل، وضعیت را بررسی کنیم.
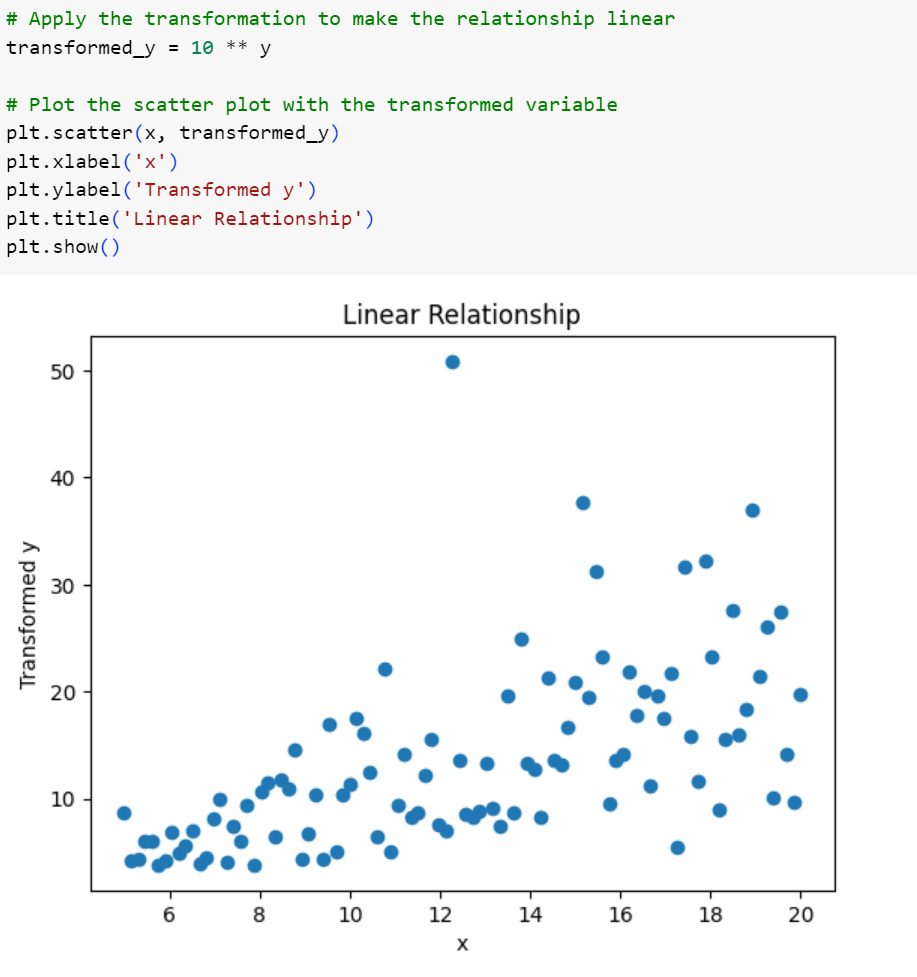
شکل 10: نمودار پراکندگی متغیرها پس از اعمال عکس تبدیل لگاریتمی
همانطور که در شکل بالا میبینیم کمی وضعیت رابطه به خطیبودن نزدیک شده است؛ اما همچنان با فرم دقیق خطی فاصله دارد. دلیل این فاصله نویز نرمالی است که در هنگام ساخت متغیر پاسخ به آن اضافه کردیم.
البته لازم به ذکر است که در کاربردهای عملی و در هنگام کار با دادههای واقعی، اگر با الگویی مشابه تصویر بالا مواجه شدید، کاملاً باید خوشحال بشوید! زیرا فضای واقعیت کمی از فضای تئوری فاصله دارد و نباید انتظار داشته باشیم که متغیرها دقیقاً بر اساس فرمهای تابعی معروفی که برای ما شناختهشده هستند رفتار کنند. نویز و همچنین نمونههای پرت در دادههای واقعی فراوان است و ما باید سعی کنیم تا از دل این بینظمیها، الگوی حاکم بر کلیت مجموعهداده را کشف و شناسایی کنیم.
مواجه با رابطهی ذاتاً ناخطی
حال اگر در مجموعهدادهمان با یک رابطهی پیچیده مواجه شدیم که با هیچکدام از تبدیلهایی که میشناسیم به فرم خطی تبدیل نشد و بهاصطلاح ذاتاً ناخطی بود، چه کار کنیم؟
در ریاضیات و در شاخهی آنالیز عددی روشهایی وجود دارند برای تقریب تابع. این روشها (مانند چندجملهای لاپلاس) تلاش میکنند تا چندجملهای مناسبی را که از تعدادی نقطه عبور میکند را شناسایی کنند. این الگوریتمها بهطورکلی به دو دستهی الگوریتمهای درونیابی و برونیابی تقسیم میشوند.
الگوریتمهای درونیابی تلاش میکنند تا چندجملهای را در یک بازهی معین شناسایی کنند؛ اما الگوریتمهای برونیابی باهدف پیشبینی رفتار منحنی در خارج از بازه دست به تخمین منحنی میزنند.
اگر چه این روشها در دنیای ریاضیات شناخته شده هستند و کاربرد خودشان را دارند، معمولاً در دنیای علم داده از این روشها استفاده نمیشود؛ زیرا این روشها گاهی پیچیدگی زیادی دارند و علاوهبرآن ممکن است دچار بیش برازش شوند. مثلاً چندجملهای لاپلاس از تمامی نقاط معرفیشده عبور میکند در صورتی این حالت اصلاً برای ما مطلوب نیست و آن را بیش برازش مینامیم.
یک راه دیگر برای تخمین روابط پیچیده، پیچیدهتر کردن مدل خطی است. در رگرسیون خطی فرض کردیم که رابطهی بین دو متغیر با یک خط قابلتوضیح است. میتوانید بهجای معادلهی خط، هر معادلهی پیچیدهای را که میخواهید جایگذاری کنید.
بهعنوانمثال میتوانید از منحنی درجه سوم یا بسط تیلور از مرتبهی دلخواه استفاده کنید. بقیهی مراحل مشابه است. کافی است تابع زیان مجموع مربعات خطا را تشکیل دهید و آن را نسبت به پارامترها بهینهسازی کنید.
نکتهای که باید به آن توجه داشته باشید این است که در این حالت دیگر تخمین پارامترها به آن سادگی و مرتبی که برای رگرسیون خطی دیدیم نخواهد بود. در رگرسیون خطی تخمین پارامترها دارای فرم بسته بود و شما بهسادگی میتوانستید با نمادهای ماتریسی آنها را بیان کنید؛ اما وقتی فرم معادله از حالت خطی خارج میشود، ریشهیابی معادله بهصورت جبری کار سادهای نخواهد بود و معمولاً برای حل آن از روشهای عددی و تقریبی استفاده میشود.
بنابراین، شما با فرایندهای محاسباتی زیادی مواجه میشوید و تخمین پارامترها کار خیلی سادهای نخواهد بود. از طرفی همچنان با خطر بیش برازش مدل روبرو هستید و ممکن است مدل روی مجموعهدادهی آزمونی عملکرد خوبی نداشته باشد.
با این اوصاف توصیهی ما این است که اگر متوجه شدید که روابط موجود در مجموعهدادهتان ذاتاً ناخطی هستند و کار کردن با آنها دشوار است، بهجای اینکه پلهپله پیچیدگی مدل رگرسیون خطی را زیاد کنید، به سراغ مدلهایی بروید که هم توانایی کشف روابط ساده را دارند و هم روابط پیچیده.
با فرض اینکه شما با شبکههای عصبی آشنایی دارید، در ادامه یک مثال ساده از این شبکهها میزنیم. توصیهی ما این است که در هنگام مواجه با روابط پیچیده، به سراغ مدلهای پیچیده؛ مانند شبکههای عصبی و جنگل تصادفی بروید. در مقالاتی جداگانه به هرکدام از این مدلها نیز خواهیم پرداخت.
مثال عملی در شبکه عصبی
در مثال زیر متغیر پاسخ را تابعی از سینوس متغیر مستقل قرار میدهیم و از توزیع نرمال نیز برای اضافهکردن نویز به آن استفاده میکنیم؛ بنابراین همانطور که در شکل زیر مشاهده میکنید، رابطه از جنس خطی نیست.
شکل 11: ایجاد و ترسیم نمودار متغیرهای مجموعه دادهی پیچیده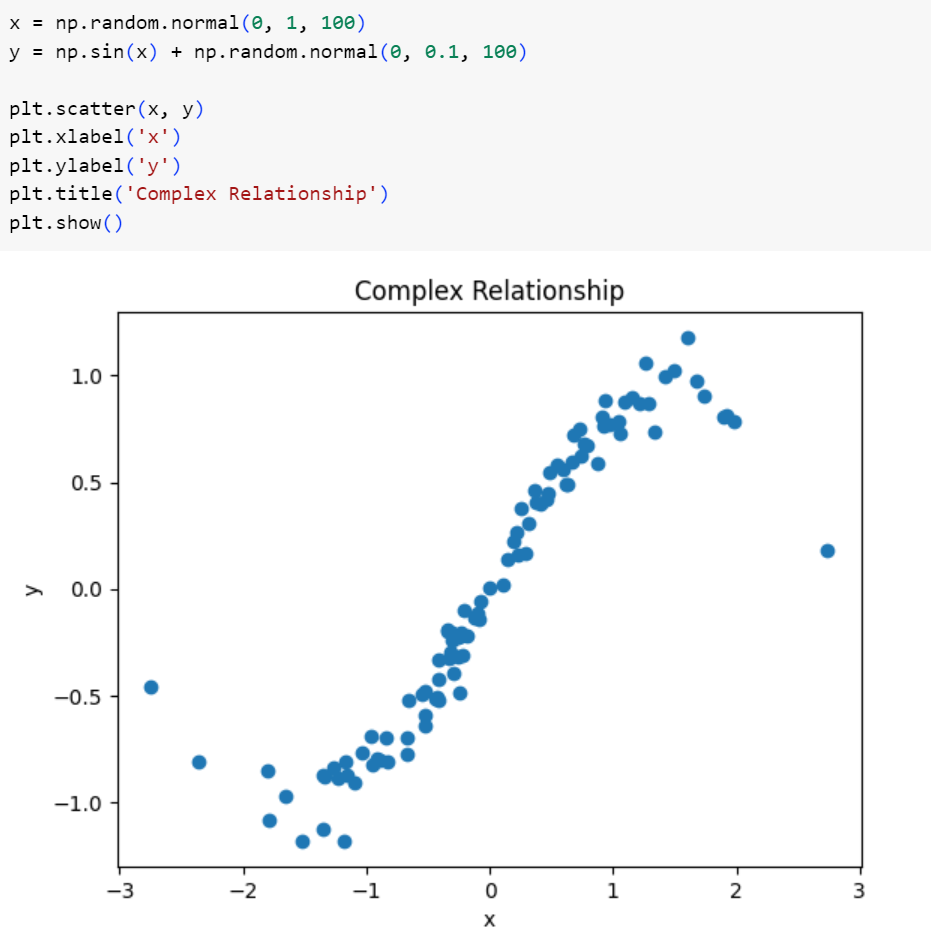
20 درصد داده را برای آزمون مدل به صورت تصادفی جدا میکنیم و از 80 درصد داده برای آموزش مدل استفاده میکنیم.
یک مدل شبکه عصبی نسبتاً ساده با دو لایهی پنهان را در نظر میگیریم و آن را 100 دور روی مجموعهدادهٔ آموزشی آموزش میدهیم

شکل 12: تعیین مجموعه دادهی آموزشی و آزمونی و مشخصات شبکهی عصبی
همانطور که در تصویر پایین مشاهده میکنید، خطای مدل روی دادهی آزمونی تقریباً برابر سه دور آخر آموزش است و مدل دچار بیش برازش نشده است.
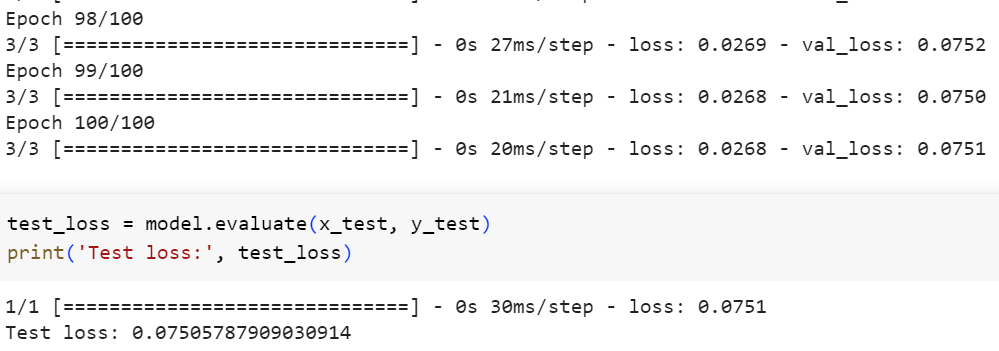
شکل 13: خطای مدل روی دورهای آخر آموزشی و مجموعه دادهی آزمونی
عملکرد مدل روی کل مجموعهداده بهصورت زیر است:
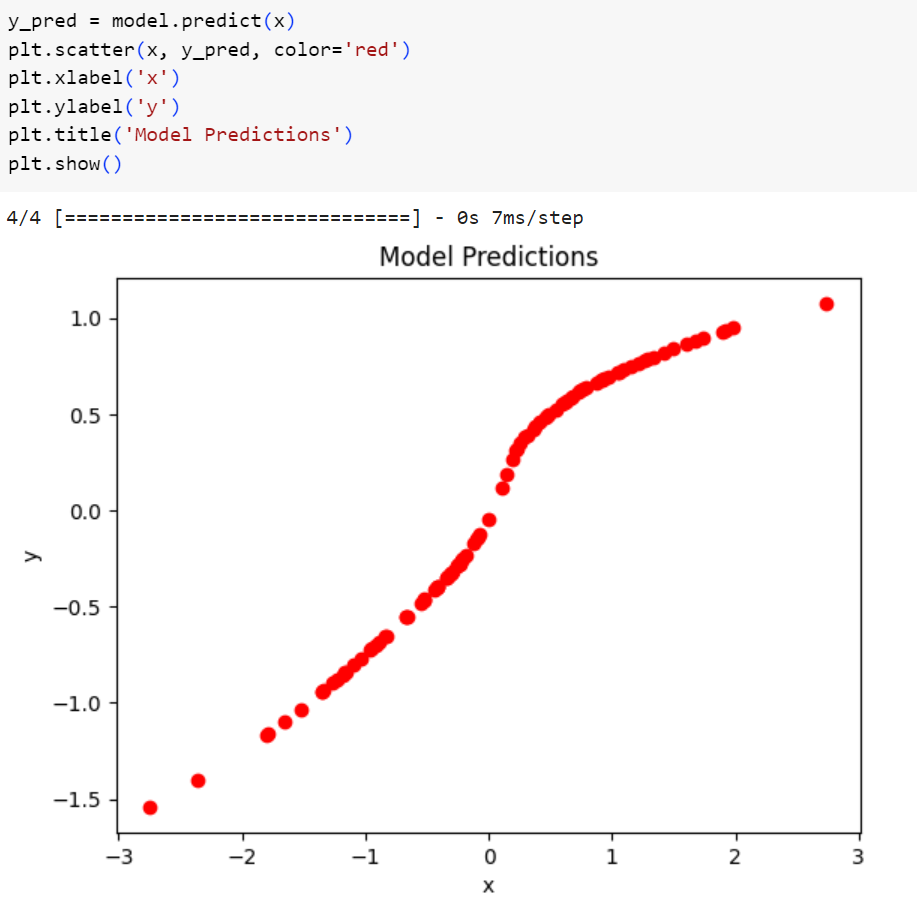
شکل 14: نمودار پیشبینیهای مدل
همانطور که مشاهده میکنید مدل بهخوبی از پس این مجموعهدادهی غیرخطی برآمده است. احتمالا امکان بهبود عملکرد این مدل نیز وجود داشته باشد اما در این پست از آن صرف نظر میکنیم زیرا هدفمان صرفا نشان دادن توانایی مدلهای مبتنی بر شبکههای عصبی در یادگیری الگوهای پیچیده بود.
در مقالات بعدی به سراغ مدلهای پیچیدهتر میرویم و تلاش میکنیم تا شما را با خصوصیات و نحوهی کارکرد هرکدام از آنها آشنا کنیم.

نظرات