آشنایی با شبکههای عصبی

آشنایی با شبکههای عصبی
شبکههای عصبی مصنوعی یا Artificial Neural Networks (ANNs) در واقع مدلهایی برای تقلید از سیستم عصبی انسانها هستند. مغز انسان یکی از شگفتیهای جهان آفرینش است. برای مثال، به دنبالهای از ارقام دستنوشته زیر توجه کنید:
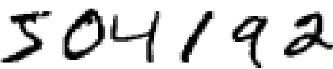
بیشتر انسانها بدون کوچکترین سختیای قادر به تشخیص ارقام موجود در این دنباله هستند: 504192. مغز انسان از یک قشر برای بینایی استفاده میکند که از 140 میلیون نورون و دهها میلیارد اتصال میان آنها تشکیل شده است. این قشر به کمک پوستههای دیگری که در مخ وجود دارد عملیات پردازش تصویر را انجام میدهد. در واقع، مغز ما ابررایانهای است که پس از صدها میلیون سال تکامل، قادر به فهم دنیای اطراف خود است. تشخیص ارقام دستنوشته کار سادهای نیست، اما توسط مغز ما به صورت کاملا خودکار انجام میشود. به گونهای که ما متوجه نیستیم که چه کار مشکلی توسط سیستم عصبی ما در حال انجام است.
میزان دشواری عمل تشخیص الگوهای دیداری زمانی روشنتر میشود که تلاش کنیم یک برنامه کامپیوتری برای مثلا تشخیص ارقام دستنوشته بالا بنویسیم. کاری که در ابتدا آسان به نظر میرسید ناگهان به عملی فوقالعاده سخت تبدیل میشود. شهودهای ساده در تشخیص اشکال (برای مثال این که رقم نه از یک حلقه در بالا و یک خط صاف در سمت راست آن تشکیل شده است) هنگام تبدیل شدن به الگوریتمهای کامپیوتری دیگر آسان به نظر نمیرسد. اگر بخواهیم این شهودها را تبدیل به قوانین دقیق نماییم، با انبوهی از استثنائات و مثالهای نقض مواجه میشویم که برای ادامه ناامیدمان میکنند. شبکههای عصبی مصنوعی برای حل چنین مسائلی طراحی شدهاند. ایده اولیه این شبکهها آن است که ابتدا تعداد بسیار زیادی از ارقام دستنوشته را به عنوان نمونههای آموزشی (training examples) جمعآوری کنیم. شکل زیر تعدادی از این نمونهها را نشان میدهد.

سپس باید یک سیستم برای یادگیری از روی نمونههای آموزشی طراحی کنیم. شبکه عصبی به دست آمده، نمونهها را برای تولید خودکار قوانین تشخیص ارقام دستنوشته به کار میگیرد. با افزایش تعداد نمونههای آموزشی، شبکه بیشتر و بیشتر راجع به ارقام دستنوشته یاد میگیرد و دقت تشخیص آن بالاتر میرود. زمانی که تعداد نمونهها به چند میلیارد عدد برسد، یک سیستم تشخیص ارقام دستنوشته با دقت عالی به دست میآید.
حال میخواهیم یک برنامه کامپیوتری بنویسیم که یک شبکه عصبی را برای تشخیص ارقام دستنوشته پیادهسازی میکند. این برنامه بدون احتساب کامنتها در مجموع تنها 74 سطر دارد و از هیچ کتابخانه خاصی درباره شبکههای عصبی استفاده نمیکند. اما همین برنامه کوتاه قادر است با دقت بالای 96 درصد و بدون دخالت انسانی، عملیات تشخیص ارقام را انجام دهد. البته الگوریتمهای دیگری وجود دارند که تشخیص ارقام را با دقت بالای 99 درصد نیز انجام میدهند که ما فعلا به آنها نمیپردازیم. در واقع، بهترین شبکههای عصبی آنقدر خوب هستند که برای پردازش چک در بانکها و تشخیص آدرس در اداره پست قابل استفاده هستند.
مسائل فراوانی برای حل توسط شبکههای عصبی وجود دارند اما تمرکز ما روی مساله تشخیص ارقام دستنوشته باقی میماند. زیرا این مساله به عنوان یک الگوی اولیه برای آزمایش انواع الگوریتمهای یادگیری به کار میرود، چرا که مسالهای چالشبرانگیز است، اما در عین حال برای حل، احتیاج به توان محاسباتی فوق بالا و یا راهحلهای فوق پیچیده ندارد. در نتیجه، ما یک شبکه عصبی را برای این مساله ارائه میدهیم، اما باید توجه داشت ایدههای استفاده شده برای آن در مسائل دیگر همچون تشخیص گفتار و یا پردازش زبانهای طبیعی نیز کاربرد دارد.
به طور خلاصه در ادامه این متن به دو مدل نورون مصنوعی به نامهای پرسپترون (perceptron) و نورون سیگمویدی (Sigmoid neuron) و یک الگوریتم متداول برای آموزش شبکههای عصبی به نام کاهش گرادیان تصادفی (Stochastic gradient descent) میپردازیم. یادگیری این مفاهیم اولیه مقدمهای بر آموزش یادگیری عمیق (Deep Learning) نیز خواهد بود.
پرسپترون
پرسپترون (perceptron) همان نورون مصنوعی در شبکههای عصبی است که برای اولین بار در دهه 1950 میلادی توسط Frank Rosenblatt طراحی شد. گرچه امروزه اقسام پیشرفتهتری از شبکههای عصبی کاربرد دارند، اما در شروع به سادهترین نوع آنها یعنی پرسپترون میپردازیم. یک پرسپترون شبکهای است که تعدادی ورودی دودویی (binary) دریافت میکند و یک خروجی دودویی تولید مینماید. شکل زیر یک پرسپترون با سه ورودی را نشان میدهد.
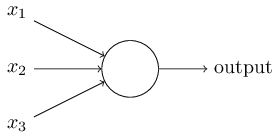
یک قانون ساده برای محاسبه خروجی وجود دارد: تعدادی عدد حقیقی به نام وزن (weight) به هر ورودی اختصاص
مییابد که نشان از میزان اهمیت آن برای شبکه دارد. در صورتی که جمع وزندار ورودیها ![]()
از یک آستانه (threshold) از پیش تعیین شده بیشتر شود، خروجی مقدار یک و در غیر این صورت مقدار صفر را میپذیرد. آستانه یک عدد حقیقی و پارامتری تعریف شده در هر پرسپترون است. به عبارت دقیقتر خروجی توسط فرمول زیر تعیین میشود:
![]()
میتوان به پرسپترون به عنوان یک مدل ریاضیاتی ساده از ابزاری نگاه کرد که با توجه به مجموعهای از شواهد
ورودی یک تصمیم قطعی میگیرد. برای مثال، تصور کنید که در تعطیلات آخر هفته قرار است یک نمایشگاه فروش محصولات خوراکی
در مرکز شهر برگزار شود. شما میخواهید تصمیم بگیرید که به این نمایشگاه بروید یا خیر. ممکن است تصمیم شما بر مبنای
معیارهای زیر باشد: آیا هوا مناسب است؟ آیا خانوادهتان مایل به همراهی شما هستند؟ آیا نمایشگاه نزدیک وسایل نقلیه
عمومی است؟ فرض کنید این سه معیار را توسط متغیرهای دودویی 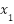 و
و
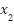 و
و 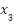 نشان میدهیم. در
صورتی که پاسخ به هر سوال بله باشد، متغیر مربوط به آن مقدار یک و در غیر این صورت مقدار صفر را میپذیرد. همچنین فرض
کنید وزن مربوط به آب و هوا مقدار 6 و وزن دو معیار دیگر مقدار 2 را برای شما داشته باشد. وزن هر معیار، مقدار اهمیت
آن را برای شما نشان میدهد. در صورتی که مقدار آستانه در نظر گرفته برابر با 5 باشد، در مدل پیادهسازی شده برای
تصمیمگیری رفتن یا نرفتن به نمایشگاه، تنها معیار اول در نظر گرفته خواهد شد و همراهی خانواده و نزدیک بودن به وسایل
نقلیه عمومی تاثیری در تصمیم نهایی نخواهند داشت.
نشان میدهیم. در
صورتی که پاسخ به هر سوال بله باشد، متغیر مربوط به آن مقدار یک و در غیر این صورت مقدار صفر را میپذیرد. همچنین فرض
کنید وزن مربوط به آب و هوا مقدار 6 و وزن دو معیار دیگر مقدار 2 را برای شما داشته باشد. وزن هر معیار، مقدار اهمیت
آن را برای شما نشان میدهد. در صورتی که مقدار آستانه در نظر گرفته برابر با 5 باشد، در مدل پیادهسازی شده برای
تصمیمگیری رفتن یا نرفتن به نمایشگاه، تنها معیار اول در نظر گرفته خواهد شد و همراهی خانواده و نزدیک بودن به وسایل
نقلیه عمومی تاثیری در تصمیم نهایی نخواهند داشت.
با تغییر وزنها و آستانه در مثال بالا میتوان مدلهای دیگری را برای تصمیمگیری طراحی نمود. در صورتی که آستانه برابر با 3 انتخاب شود، پرسپترون زمانی تصمیم به رفتن به نمایشگاه را میگیرد که یا هوا خوب باشد یا هم خانواده شما را همراهی کنند و هم نمایشگاه نزدیک وسایل عمومی باشد. در نتیجه کاهش آستانه به معنای تمایل بیشتر برای رفتن به نمایشگاه است.
واضح است که یک پرسپترون نمیتواند مدل کاملی از سیستم تصمیمگیری مغز انسان باشد. این شبکه تنها نشان میدهد که چگونه میتوان از تجمیع شواهد گوناگون را برای گرفتن یک تصمیم نهایی استفاده کرد. در کنار هم قرار دادن تعداد بیشتری از این نورونهای مصنوعی شبکههای عصبی پیچیدهتری را به دست خواهند داد:
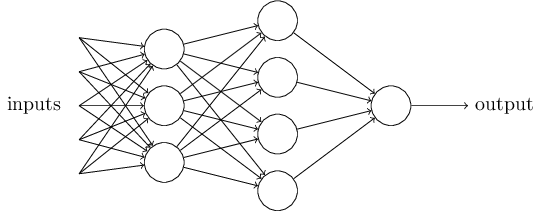
در این شبکه، هر ستون از پرسپترونها یک لایه (layer) نامیده میشود. لایه اول برای جمع زدن شواهد ورودی به کار میرود. اما لایه دوم چه معنایی دارد؟ تصمیمگیری بر مبنای تصمیمات به دست آمده از نورونهای لایه اول! این تصمیمات نتایج به کار بردن پیچیدگیها و انتزاعات بیشتر توسط شبکه هستند. هرچه تعداد لایهها بیشتر شود، تفسیر فرآیند تصمیمگیری پیچیدهتر خواهد شد. همانطور که در شبکه نمونه بالا مشاهده میشود، خروجی یک پرسپترون میتواند به عنوان ورودی چندین پرسپترون دیگر به کار رود. شبکه نهایی نیز میتواند چندین خروجی داشته باشد که هرکدام نماینده یک تصمیم هستند.
فرمول اصلی به کار رفته در پرسپترون (![]() ) نیز میتواند سادهسازی
شود. به کار بردن نمادهای برداری
) نیز میتواند سادهسازی
شود. به کار بردن نمادهای برداری ![]() و
و ![]() به جای دنباله ورودیها و وزنها، و نماد ضرب داخلی بین دو بردار به جای عبارت
اولیه، و استفاده از متغیر بایاس (bias) به جای منفی آستانه، فرمول تصمیمگیری پرسپترون را به صورت زیر
درمیآورد:
به جای دنباله ورودیها و وزنها، و نماد ضرب داخلی بین دو بردار به جای عبارت
اولیه، و استفاده از متغیر بایاس (bias) به جای منفی آستانه، فرمول تصمیمگیری پرسپترون را به صورت زیر
درمیآورد:
![]()
در این فرمول، بایاس نشاندهنده میزان آسانی روشن شدن (fire) پرسپترون است. به معنای دیگر، هرچه بایاس بیشتر باشد، برای پرسپترون آسانتر خواهد بود که خروجی یک را تولید کند.
یکی دیگر از کاربردهای پرسپترون توصیف توابع منطقی سادهای چون AND، OR و NAND است. برای مثال، شکل زیر پرسپترونی را با دو ورودی با وزن 2- و بایاس 3 نشان میدهد. در صورتی که حداقل یکی از دو ورودی صفر باشند، خروجی یک خواهد بود. اما اگر هر دو ورودی یک باشند، خروجی صفر خواهد بود. در نتیجه این پرسپترون یک گیت NAND را نشان میدهد.
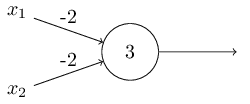
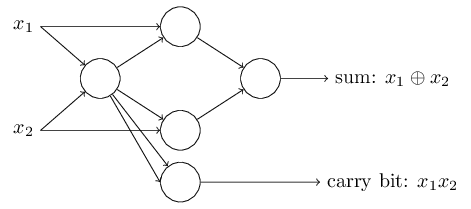
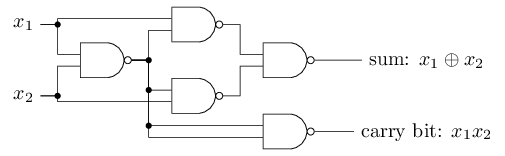
مثال بالا نشان میدهد که میتوان شبکهای از پرسپترونها را برای محاسبه هرگونه تابع منطقی طراحی کرد. دلیل آن این است که گیت NAND به تنهایی میتواند برای محاسبه تمامی توابع منطقی به کار رود. مثال زیر یک مدار منطقی و یک شبکه عصبی (با فرض پرسپترونهای با وزن 2- و بایاس 3) را نشان میدهد که معادل یکدیگر هستند.
|
|
|
یکی دیگر از راههای نمایش شبکههای عصبی، قرار دادن متغیرهای ورودی در یک لایه شبیه به لایه پرسپترونها است، که به آن لایه ورودی (input layer) میگویند. همچنین به جای دو ورودی با وزن 2- در یکی از پرسپترونهای شبکه بالا میتوان یک ورودی با وزن 4- داشت.
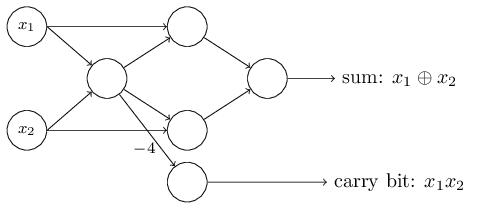
نکتهای که شبکههای عصبی را از مدارهای منطقی متمایز میکند، استفاده از الگوریتمهای یادگیری بر روی این شبکهها است. شبکههای عصبی قادر به حل مسائل مختلفی هستند که در اکثر موارد طراحی یک مدار منطقی برای حل آنها بسیار بسیار دشوار خواهد بود.
نورون سیگمویدی
یک بار دیگر مثال تشخیص ارقام دستنوشته را در نظر بگیرید. فرض کنید شبکهای از پرسپترونها داریم که میخواهیم به وسیله آن این مساله را حل کنیم. ورودیهای شبکه، پیکسلهای تصویر اسکن شده یک رقم دستنوشته هستند. شبکه باید وزنها و بایاسهای پرسپترونها را به گونهای یاد بگیرد که خروجی آن، دستهبندی درستی از رقم مذکور باشد. در شبکه ایدهآل، یک تغییر کوچک در یکی از وزنها باید تغییر کوچکی در خروجی ایجاد کند. اساس کار آموزش شبکه به این صورت است که وزنها و بایاسها در مواجهه با نمونههای آموزشی جدید هر بار کمی بهبود مییابند تا به مرور خروجیهای درستتری تولید شود.
نورون سیگمویدی (Sigmoid neuron) نوعی نورون مصنوعی به کار رفته در شبکههای عصبی است که مشابه پرسپترون میباشد. با این تفاوت که اعمال یک تغییر کوچک روی یکی از وزنها یا بایاس آن، تغییر کوچکی در خروجی آن ایجاد میکند (برخلاف پرسپترون که گاهی این تغییر منجر به دگرگون شدن خروجی آن میشود). همین تفاوت، باعث میشود شبکه به وجود آمده از نورونهای سیگمویدی قادر به یادگیری باشد.
خروجی نورون سیگمویدی به جای صفر یا یک، مقداری بین آن دو است. ورودیهای آن نیز میتوانند هر مقداری بین
صفر تا یک داشته باشند. خروجی نورون با ورودیهای ![]() و وزنهای
و وزنهای
![]() و بایاس
و بایاس ![]() طبق فرمول
زیر محاسبه میشود.
طبق فرمول
زیر محاسبه میشود.
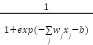
تابع ![]() تابع سیگموید نام دارد. در این تابع، هرچه مقدار
تابع سیگموید نام دارد. در این تابع، هرچه مقدار
![]() بزرگتر باشد، خروجی نورون به 1 نزدیکتر خواهد بود و هرچه مقدار z
منفیتر باشد، خروجی به صفر نزدیکتر میشود. درنتیجه، نورون سیگمویدی بسیار شبیه به پرسپترون عمل میکند. تنها تفاوت آن
است که تابع سیگموید، خروجی نورون را نرمتر میکند و از تغییرات ناگهانی جلوگیری میکند. در صورتی که تغییرات خروجی
نورون را توسط
بزرگتر باشد، خروجی نورون به 1 نزدیکتر خواهد بود و هرچه مقدار z
منفیتر باشد، خروجی به صفر نزدیکتر میشود. درنتیجه، نورون سیگمویدی بسیار شبیه به پرسپترون عمل میکند. تنها تفاوت آن
است که تابع سیگموید، خروجی نورون را نرمتر میکند و از تغییرات ناگهانی جلوگیری میکند. در صورتی که تغییرات خروجی
نورون را توسط![]() نشان دهیم، این مقدار توسط فرمول زیر (با کمک گرفتن
از مشتقات جزئی خروجی نسبت به متغیرها) به طور تقریبی محاسبه میشود:
نشان دهیم، این مقدار توسط فرمول زیر (با کمک گرفتن
از مشتقات جزئی خروجی نسبت به متغیرها) به طور تقریبی محاسبه میشود:
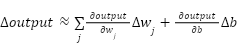
طبق این فرمول، ![]() نسبت به تغییرات وزنها (
نسبت به تغییرات وزنها (![]() ) و تغییرات بایاس (
) و تغییرات بایاس (![]() ) یک تابع خطی خواهد
بود.
) یک تابع خطی خواهد
بود.
به جای تابع سیگموید میتوان از دیگر توابع فعالسازی (activation functions) نیز برای نرم کردن خروجی استفاده نمود. مزیت سیگموید مشتقپذیر بودن آن به دلیل به کارگیری تابع نمایی توسط آن است. در صورتی که مایل باشیم خروجی نورون یک مقدار صفر و یکی را تولید نماید، باید یک آستانه نهایی (مثلا 0.5) برای آن تعیین نمود. در صورتی که خروجی بیشتر از آستانه باشد آن را به یک و در غیر این صورت به صفر تفسیر میکنیم. از دیگر توابع فعالسازی مشهور میتوان به tanh و softmax اشاره کرد.
معماری شبکه عصبی
در این قسمت یک شبکه عصبی برای دستهبندی (classification) ارقام دستنوشته ارائه میدهیم. ابتدا چند اصطلاح را در این زمینه بررسی مینماییم.
لایه پنهان (hidden layer): هر لایهای از نورونها که در میان لایه ورودی و لایه خروجی از شبکه قرار میگیرد لایه پنهان نام دارد. شکل زیر شبکهای دارای چهار لایه را نشان میدهد که دو تا از آنها لایه پنهان میباشند. این شبکه، یک پرسپترون چند لایه (Multilayer Perceptron) یا MLP نام دارد، هرچند که نورونهای آن سیگمویدی (و نه پرسپترون معمولی) هستند.
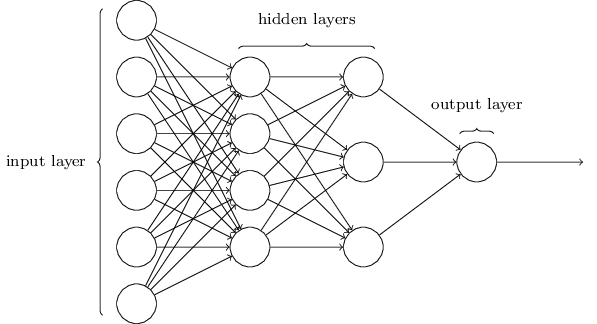
شبکه رو به جلو (feedforward network): شبکهای که در آن خروجی هر لایه، ورودی لایه بعد است. به عبارت دیگر، در آن حلقه (loop) وجود ندارد. در نتیجه اطلاعات استنتاج شده توسط شبکه همیشه رو به جلو حرکت میکند و به عقب باز نمیگردد. در مقابل، شبکههای دارای حلقه قرار میگیرند که شبکههای بازگشتی (recurrent networks) نامیده میشوند. در این شبکهها بحث زمان اهمیت پیدا میکند. زیرا ممکن است یک نورون مدت کوتاهی روشن و سپس خاموش شود. شبکههای بازگشتی نسبت به شبکههای رو به جلو، عملکردی شبیهتر به مغز انسان دارند، و گاهی مسائلی را به سادگی حل میکنند که در صورت به کار بردن شبکههای رو به جلو پیچیدگی شبکه بسیار زیاد خواهد شد. اما تمرکز متن فعلی بر روی شبکههای رو به جلو است که سادهتر میباشند.
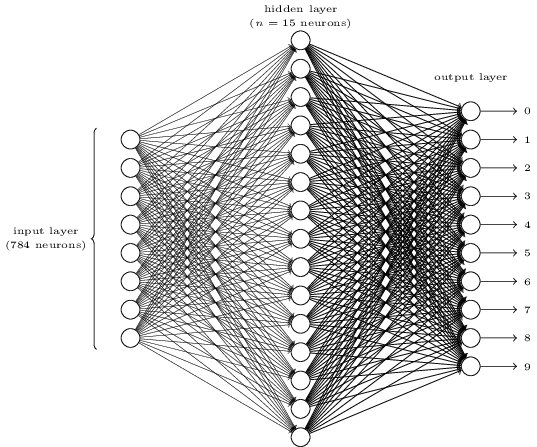
حال به مساله تشخیص ارقام دستنوشته برمیگردیم. فرض کنیم ورودی مساله، یک تصویر سیاه سفید از تنها یک رقم و دارای 28⨯28 پیکسل باشد. در نتیجه 784 نورون ورودی خواهیم داشت که هرکدام عددی میان 0 و 1 (میزان سیاه بودن پیکسل خاکستری) را دارا میباشند. لایه خروجی به ازای هر رقم یک نورون دارد که هرکدام خروجی بزرگتری تولید کنند، تصویر برابر با رقم متناظر با آن تشخیص داده میشود.
استفاده از نورونهای بیشتر در لایههای پنهان منجر به دقیقتر شدن تشخیص شبکه میشود. اما از طرف دیگر زمان آموزش (train) آن را نیز افزایش میدهد. پس باید در تصمیمگیری برای تعداد نورونها هنگام طراحی شبکه دقت نمود. شبکهای که در این قسمت آن را به کار میبریم دارای یک لایه پنهان با 15 نورون و به شکل زیر است.
یک روش دیگر برای طراحی شبکه، به کاربردن تنها چهار خروجی دودویی است. این خروجیها میتوانند معرف
![]() حالت مختلف باشند که باید دیکد شوند. از آنجایی که این مقدار عددی
بزرگتر از 10 است برای نمایش ده رقم کافی میباشد. اما نتیجه پیادهسازی دو معماری فوق به صورت تجربی نشان میدهد که
استفاده از ده خروجی متمایز دقت بیشتری به دست میدهد. اما چرا این طور است؟ پاسخ به این سوال به ما کمک میکند ساز و
کار شبکههای عصبی را درک کنیم. هر نورون خروجی در شبکه عصبی اول (دارای ده خروجی) تلاش میکند شواهدی را جمعآوری کند
که نشان دهد تصویر ورودی مطابق با رقم متناظر با نورون خروجی است. نورونهای لایه پنهان نیز به جمعآوری این شواهد کمک
میکنند. برای مثال اگر لایه پنهان اشکال زیر را در تصویر ورودی تشخیص دهد، به احتمال زیاد نورون خروجی متناظر با رقم
0 روشن خواهد شد.
حالت مختلف باشند که باید دیکد شوند. از آنجایی که این مقدار عددی
بزرگتر از 10 است برای نمایش ده رقم کافی میباشد. اما نتیجه پیادهسازی دو معماری فوق به صورت تجربی نشان میدهد که
استفاده از ده خروجی متمایز دقت بیشتری به دست میدهد. اما چرا این طور است؟ پاسخ به این سوال به ما کمک میکند ساز و
کار شبکههای عصبی را درک کنیم. هر نورون خروجی در شبکه عصبی اول (دارای ده خروجی) تلاش میکند شواهدی را جمعآوری کند
که نشان دهد تصویر ورودی مطابق با رقم متناظر با نورون خروجی است. نورونهای لایه پنهان نیز به جمعآوری این شواهد کمک
میکنند. برای مثال اگر لایه پنهان اشکال زیر را در تصویر ورودی تشخیص دهد، به احتمال زیاد نورون خروجی متناظر با رقم
0 روشن خواهد شد.
|
|
|
|
از مثال بالا میتوان نتیجه گرفت یک الگوریتم یادگیری خوب در پردازش تصویر باید بتواند نورونهای پنهان را وادار کند اشکال جزئی به کار رفته در تصاویر ورودی را بیایند. این کار به کمک تعیین وزنهای ورودی برای هر نورون پنهان و خروجی صورت میپذیرد. همچنین میتوان نتیجه گرفت استفاده از مکاشفات (heuristics) در طراحی شبکههای عصبی بسیار حائز اهمیت است.
الگوریتم کاهش گرادیان
در این بخش الگوریتم کاهش گرادیان (Gradient Descent) را توضیح میدهیم که روشی برای یادگیری وزنها در
شبکه عصبی است. فرض کنیم ورودی شبکه تشخیص ارقام دستنوشته، بردار ![]() دارای 784 عنصر باشد. برچسب هر بردار نیز به شکل
دارای 784 عنصر باشد. برچسب هر بردار نیز به شکل ![]() است که تنها در یکی از ارقام مقدار یک را دارد. در هر مرحله از آموزش شبکه و
پس از تعیین مجموعه وزنها (w) و مجموعه بایاسها (b) برای آن، برای آن که صحت عملکرد شبکه را اندازهگیری کنیم از تابع
هزینه (cost function) زیر استفاده میکنیم.
است که تنها در یکی از ارقام مقدار یک را دارد. در هر مرحله از آموزش شبکه و
پس از تعیین مجموعه وزنها (w) و مجموعه بایاسها (b) برای آن، برای آن که صحت عملکرد شبکه را اندازهگیری کنیم از تابع
هزینه (cost function) زیر استفاده میکنیم.
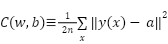
در فرمول فوق متغیر n تعداد نمونههای آموزشی و a بردار خروجی شبکه را به ازای ورودی x نشان میدهند. عبارت
![]() نیز طول بردار
نیز طول بردار ![]() را
نشان میدهد. تابع هزینه فوق خطای میانگین مربعات (mean squared error) یا MSE نام دارد که تابعی درجه دوم و همواره
غیرمنفی است. هرچه مقدار این تابع کوچکتر باشد یعنی خطای تشخیص کمتر بوده است. در نتیجه هدف الگوریتم یادگیری کاهش
تابع هزینه است. استفاده از یک تابع درجه دو مانند تابع فوق (به جای اندازهگیری مستقیم درصد رقمهای درست تشخیص داده
شده) به نرم شدن فرآیند یادگیری (تغییر جزئی خروجی به ازای تغییر جزئی ورودی) کمک میکند.
را
نشان میدهد. تابع هزینه فوق خطای میانگین مربعات (mean squared error) یا MSE نام دارد که تابعی درجه دوم و همواره
غیرمنفی است. هرچه مقدار این تابع کوچکتر باشد یعنی خطای تشخیص کمتر بوده است. در نتیجه هدف الگوریتم یادگیری کاهش
تابع هزینه است. استفاده از یک تابع درجه دو مانند تابع فوق (به جای اندازهگیری مستقیم درصد رقمهای درست تشخیص داده
شده) به نرم شدن فرآیند یادگیری (تغییر جزئی خروجی به ازای تغییر جزئی ورودی) کمک میکند.
در الگوریتم کاهش گرادیان، برای بروزرسانی وزن دلخواه ![]() و بایاس
و بایاس ![]() از فرمولهای زیر
استفاده میکنیم. با اعمال روش فوق به صورت مکرر در جهت مشتق جزئی تابع هزینه نسبت به هر متغیر، از مقدار آن متغیر
میکاهیم. در نتیجه در هر بار تکرار الگوریتم تابع هزینه مقداری کاهش مییابد.
از فرمولهای زیر
استفاده میکنیم. با اعمال روش فوق به صورت مکرر در جهت مشتق جزئی تابع هزینه نسبت به هر متغیر، از مقدار آن متغیر
میکاهیم. در نتیجه در هر بار تکرار الگوریتم تابع هزینه مقداری کاهش مییابد.
![]()
![]()
یکی از بزرگترین چالشها در الگوریتم کاهش گرادیان آن است که مشتقات باید روی تعداد زیادی از نمونهها گرفته شوند و این کار برای مجموعه بزرگی از نمونههای آموزشی امکانپذیر نیست. در الگوریتم کاهش گرادیان تصادفی، هر بار بخشی کوچک و تصادفی از نمونهها انتخاب میشود و عملیات کاهش گرادیان روی آن اعمال میگردد تا سرعت یادگیری بالا رود. این مجموعههای کوچکتر، دسته کوچک (mini-batch) نامیده میشوند.
پیادهسازی شبکه برای تشخیص ارقام دستنوشته
در این بخش میخواهیم مساله تشخیص ارقام را بر روی مجموعه داده MNIST توسط زبان برنامهنویسی پایتون پیادهسازی کنیم. این مجموعه داده از 60000 نمونه آموزشی و 10000 نمونه آزمایشی تشکیل شده است. تنها کتابخانه مورد نیاز پایتون در این کد Numpy است که باید قبل از مطالعه ادامه متن آن را نصب کنید.
اولین قطعه کد به شکل زیر است:
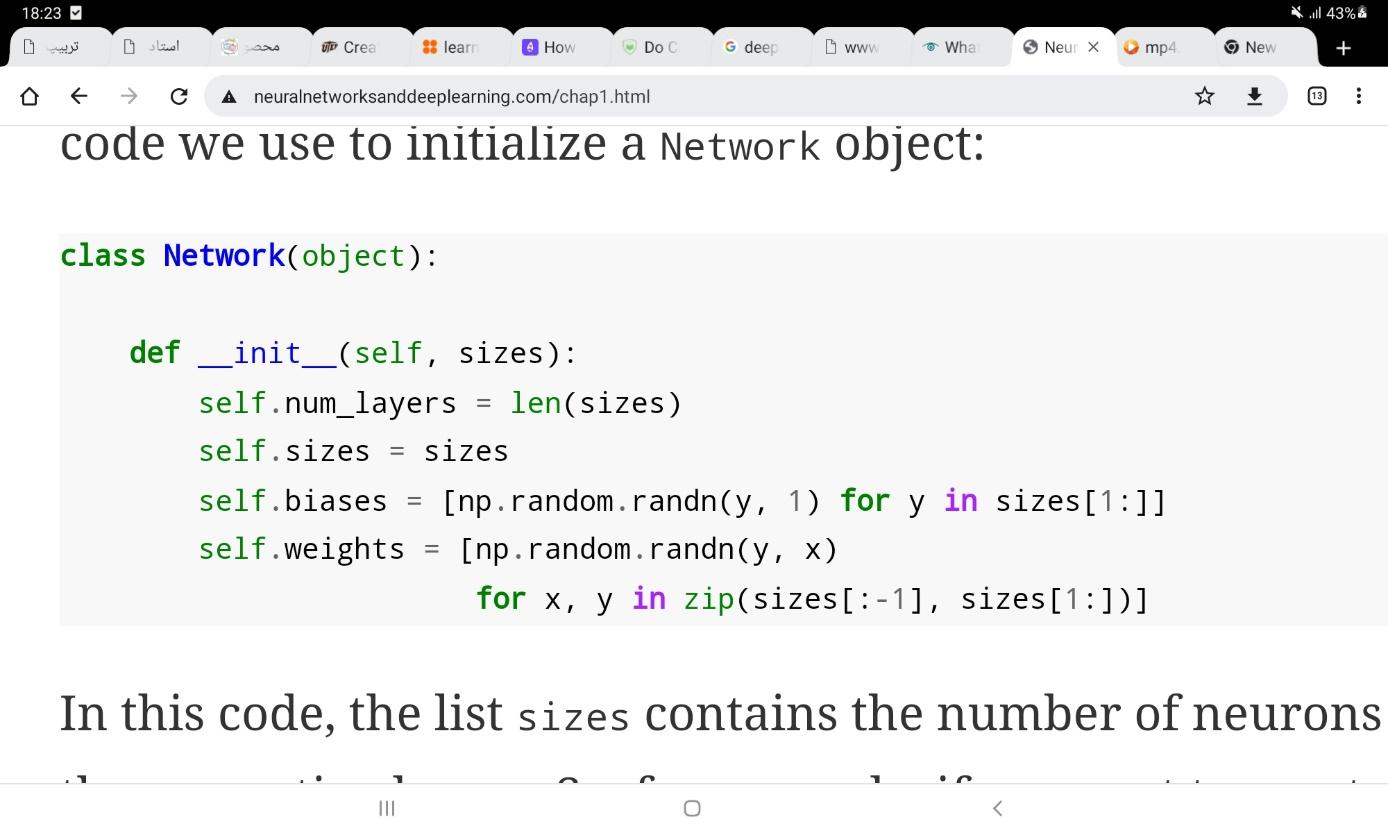
در کد فوق، کلاس Network را تعریف میکنیم که تعداد نورونهای هر لایه را به وسیله sizes دریافت میکند.
(برای مثال اگر بخواهیم یک شبکه با دو ورودی، سه نورون در لایه پنهان و یک خروجی داشته باشیم، باید از عبارت
net=Network([2,3,1]) استفاده کنیم.) وزنها و بایاسهای شبکه همه به صورت تصادفی توسط تابع گاوسی randn مقداردهی
میشوند. از آنجایی که لایه اول، لایه ورودی است، وزنی برای آن مقداردهی نمیشود. در این کد net.weights[m] یک ماتریس
است که درایه ![]() آن، وزن یال اتصال دهنده نورون k ام در لایه (m-1)
ام را به نورون j ام در لایه m ام نشان میدهد. حال باید تابع feedforward را برای شبکه تعریف کنیم. این کار در قطعه
کد زیر انجام گرفته است:
آن، وزن یال اتصال دهنده نورون k ام در لایه (m-1)
ام را به نورون j ام در لایه m ام نشان میدهد. حال باید تابع feedforward را برای شبکه تعریف کنیم. این کار در قطعه
کد زیر انجام گرفته است:

در این قطعه کد، بردار ورودی a از نورونهای سیگمویدی شبکه عبور میکند و خروجی شبکه تولید میشود. تابع سیگموید باید به صورت جداگانه به شکل زیر تعریف شود:

در این کد z یک آرایه Numpy است که تابع سیگموید بر روی هر یک از عناصر آن به صورت مجزا اعمل میشود.
در نهایت الگوریتم یادگیری کاهش گرادیان تصادفی باید به شکل زیر روی شبکه اعمال شود:

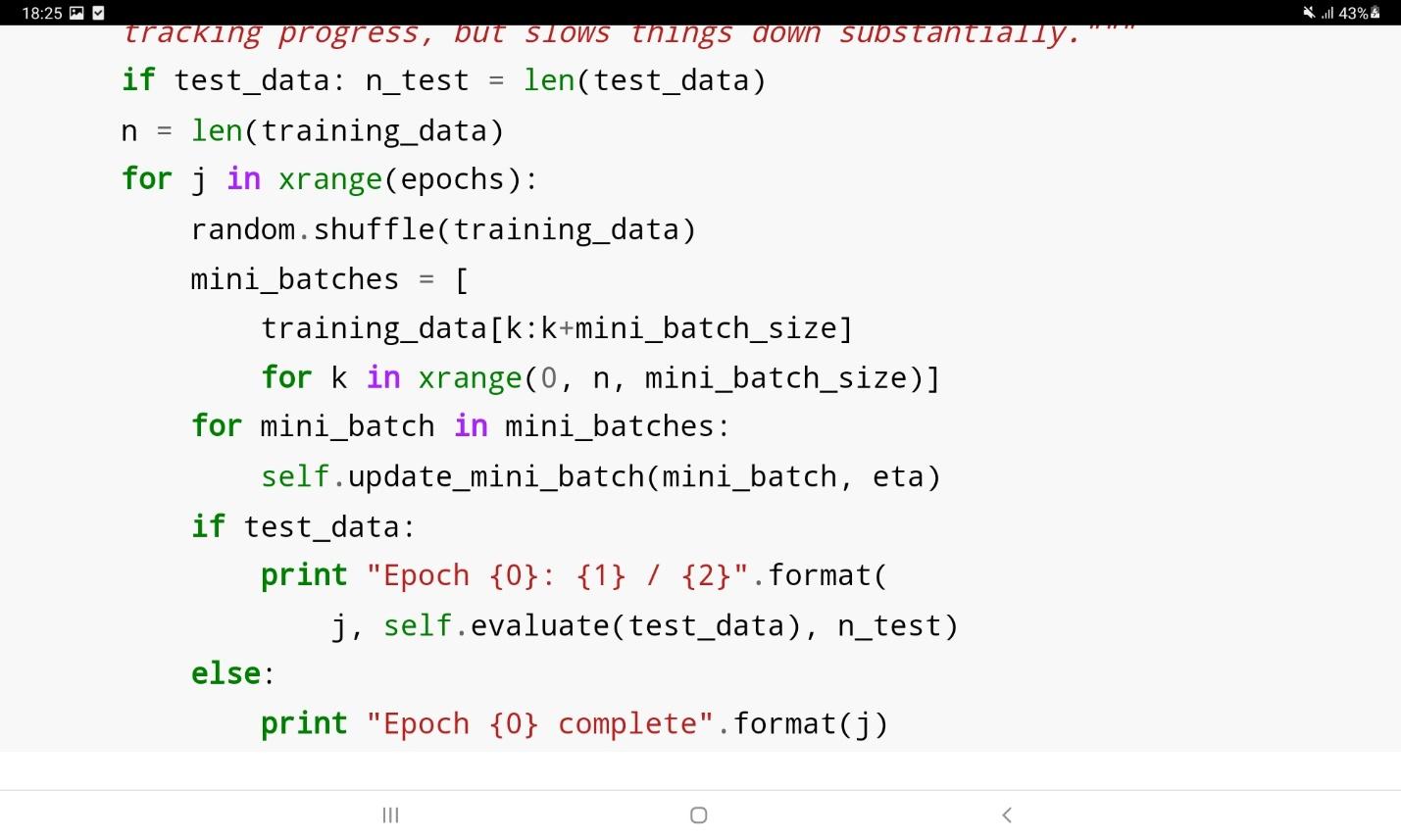
در این قطعه کد، مجموعه آموزشی training_data نام دارد که از دوتایی ورودیهای آموزشی شبکه به همراه خروجیهای مطلوب آن تشکیل شده است. متغیر epochs تعداد دفعات آموزش شبکه بر روی کل مجموعه آموزشی را نشان میدهد. متغیر mini_batch_size نیز اندازه دستههای کوچک نمونهگیری را در هر بار بروزرسانی شبکه نشان میدهد. متغیر eta نرخ یادگیری است. متغیر test_data در صورتی که مثبت باشد، پس از هر بار آموزش شبکه، یک ارزیابی روی عملکرد آن به صورت زیر انجام میدهد.
در تابع ارزیابی تعداد نمونههای آزمایشی که درست تشخیص داده شوند نسبت به تعداد کل نمونهها محاسبه میشوند. برچسبی که برای یک نمونه تشخیص داده میشود متناظر با آن نورون خروجی شبکه است که بزرگترین مقدار خروجی را داشته باشد.

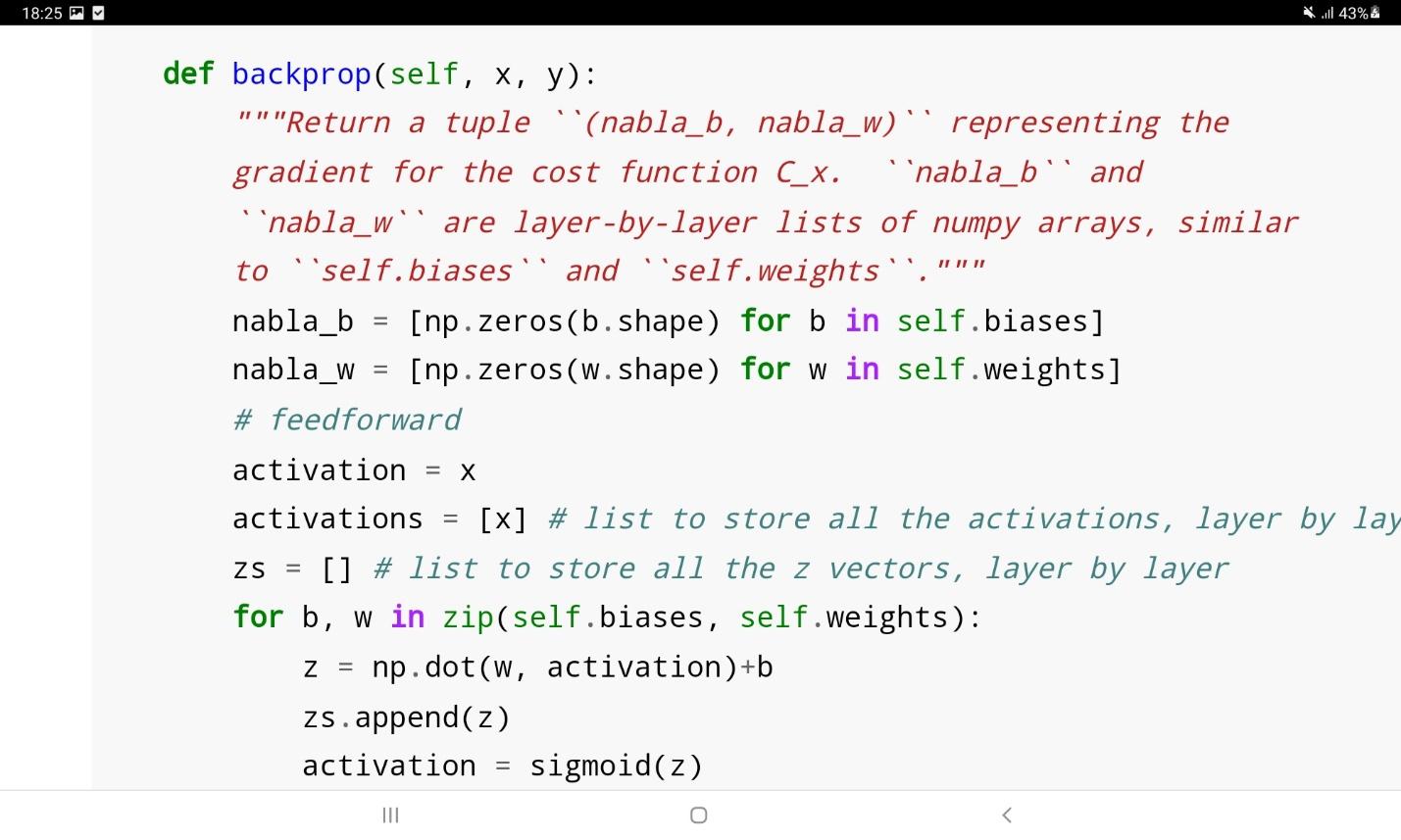
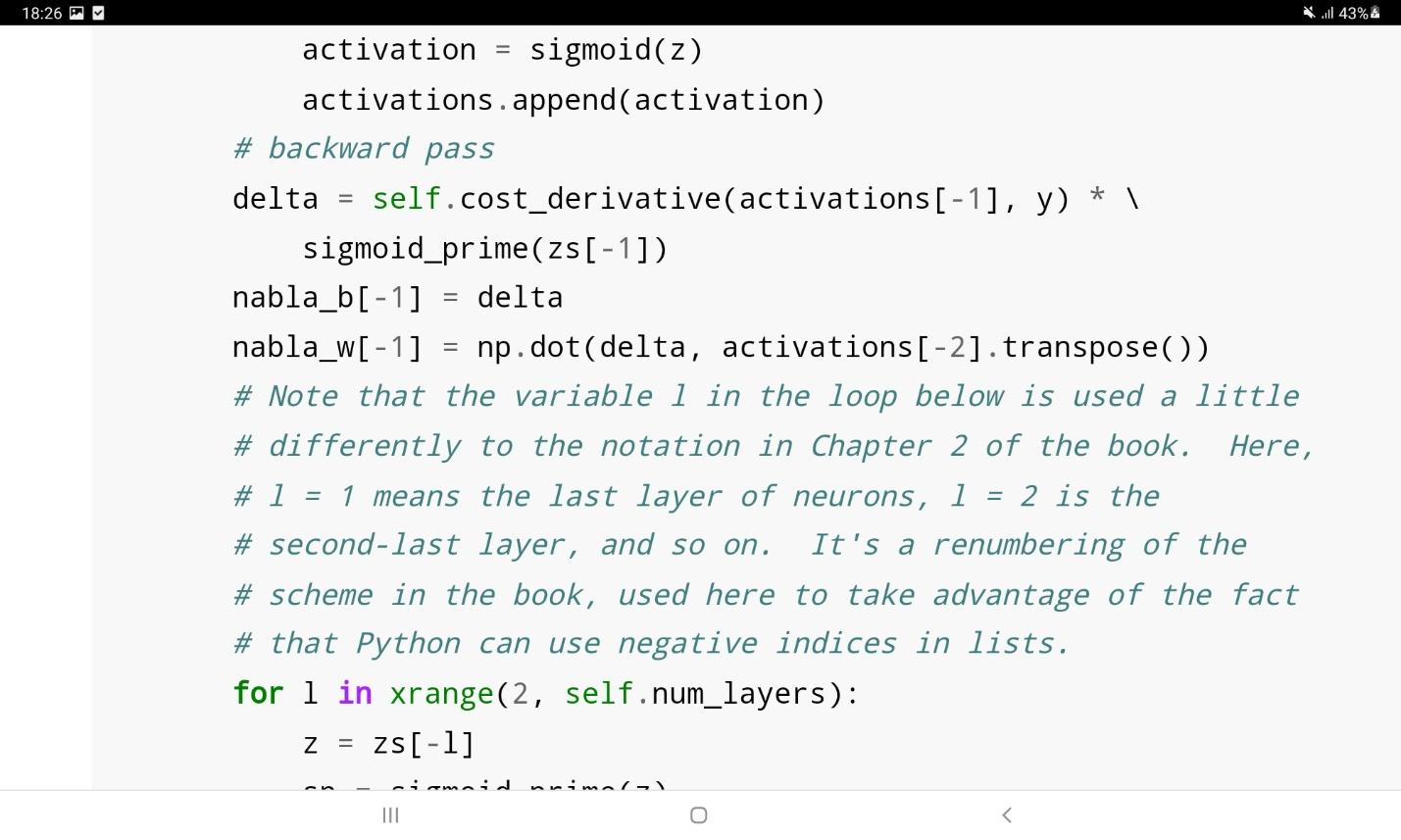
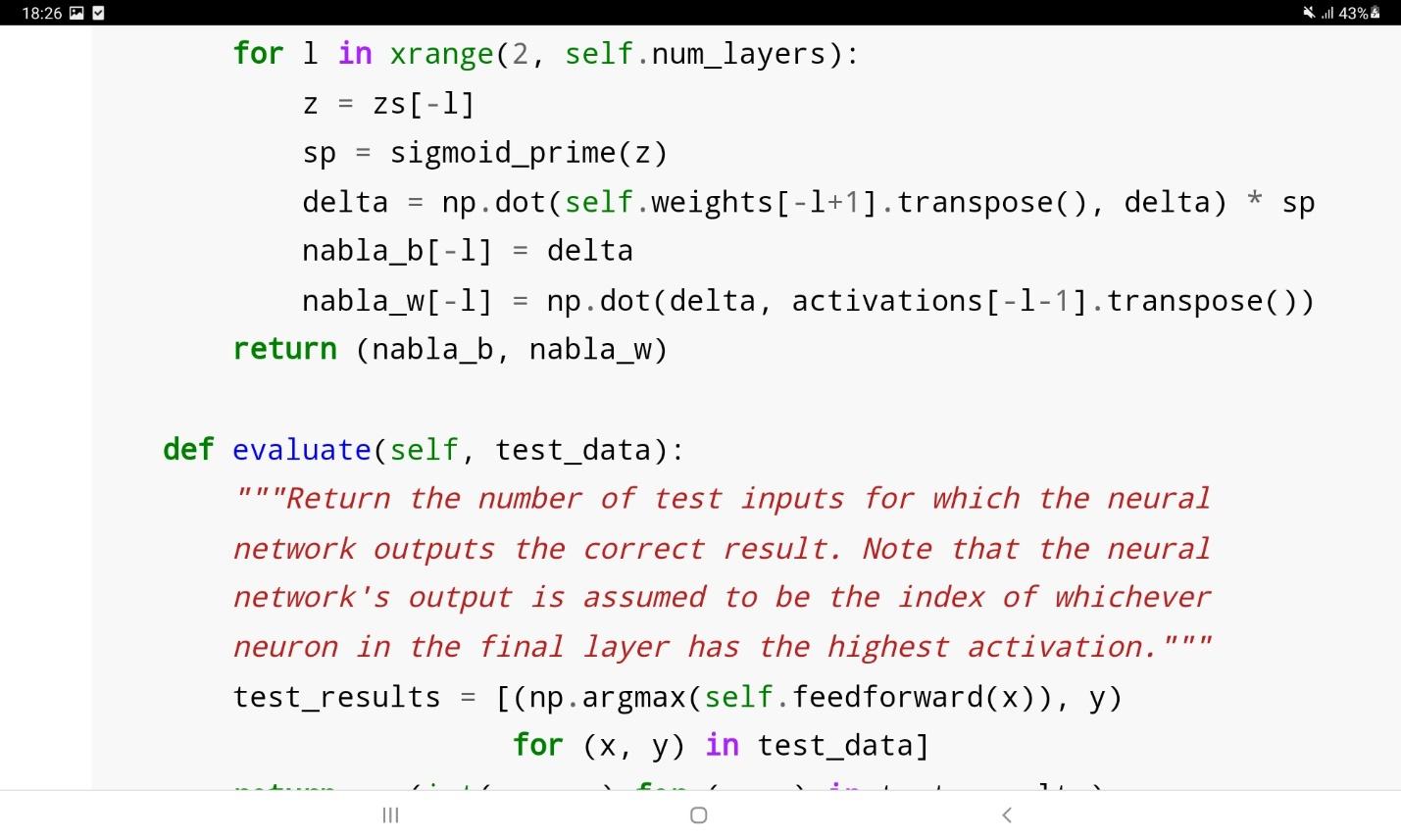
مهمترین بخش الگوریتم SGD در کد فوق، تابع update_mini_batch است که پیادهسازی آن در ادامه مشاهده میشود:
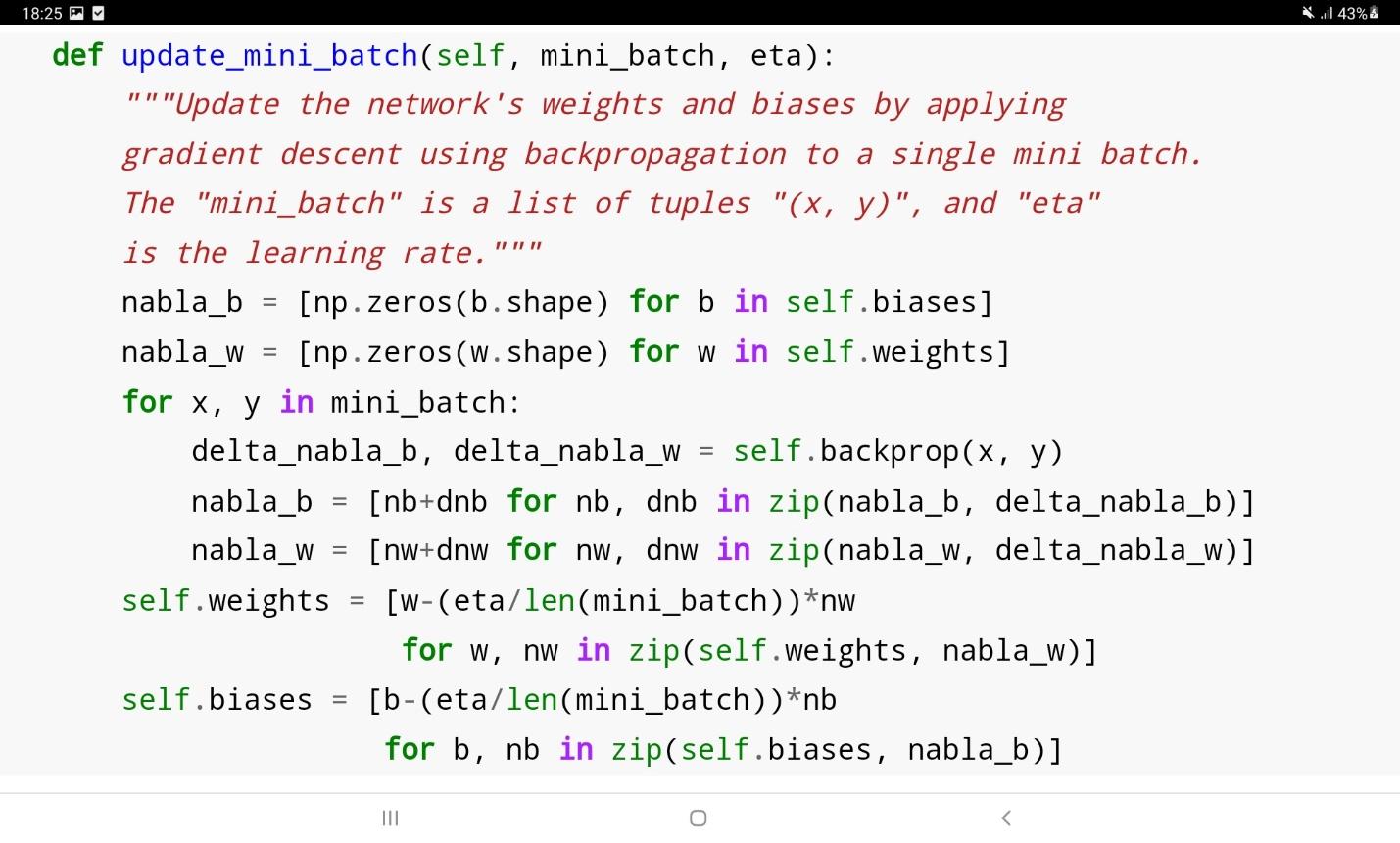
در این کد وزنها و بایاسهای شبکه با یک بار اعمال الگوریتم کاهش گرادیان بروزرسانی میشوند. تابع backprop در قطعه کد بالا، الگوریتم backpropagation را فراخوانی میکند تا گرادیان تابع هزینه را محاسبه نماید.

حال، عملکرد شبکه فوق را روی مجموعه داده MNIST میسنجیم. برای بارگذاری این مجموعه داده میتوان از کد زیر استفاده نمود:
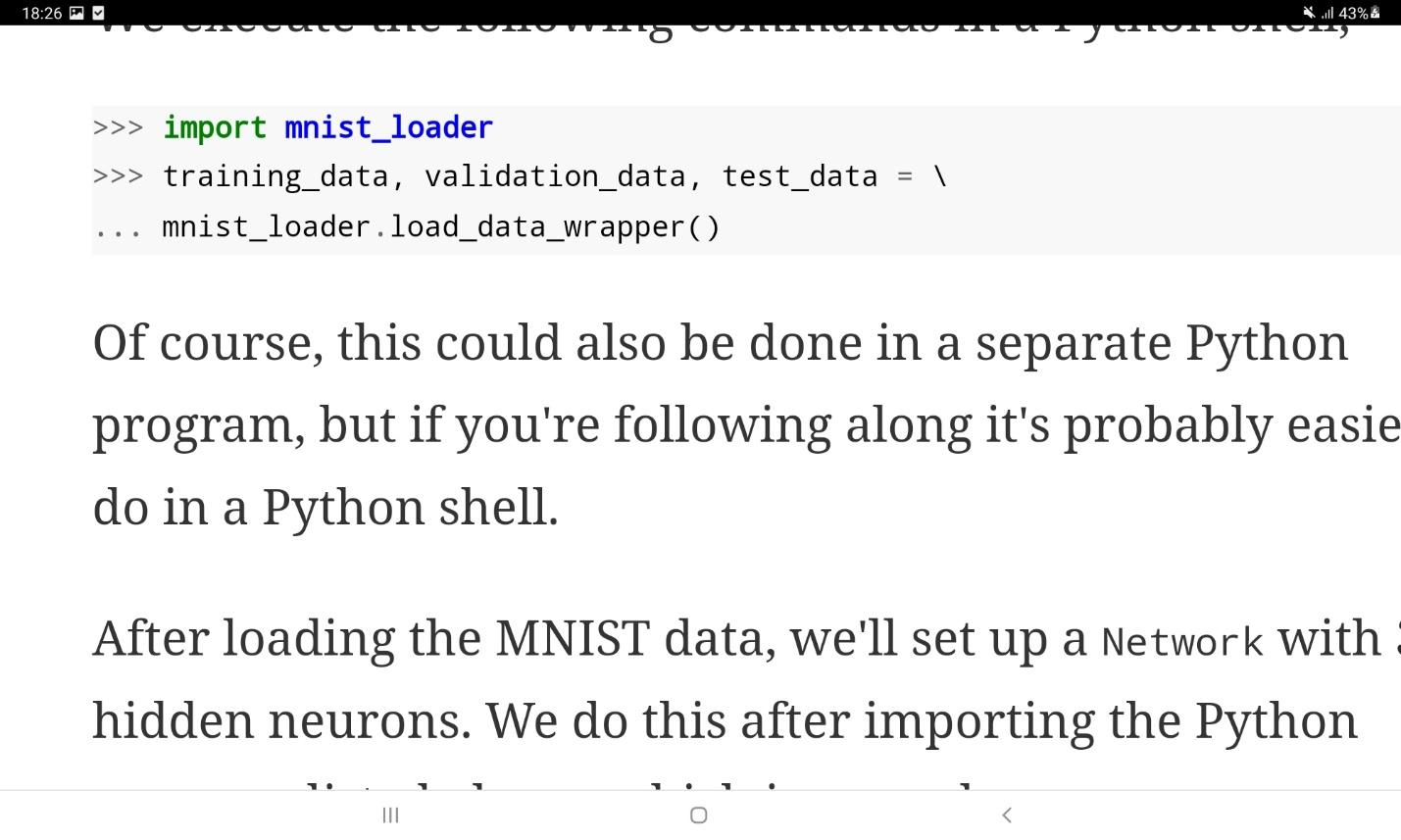
در ادامه یک شبکه با تعداد 30 نورون پنهان تعریف میکنیم و شبکه را طی 30 مرحله، با اندازه دسته 10 و نرخ یادگیری 3 آموزش میدهیم.
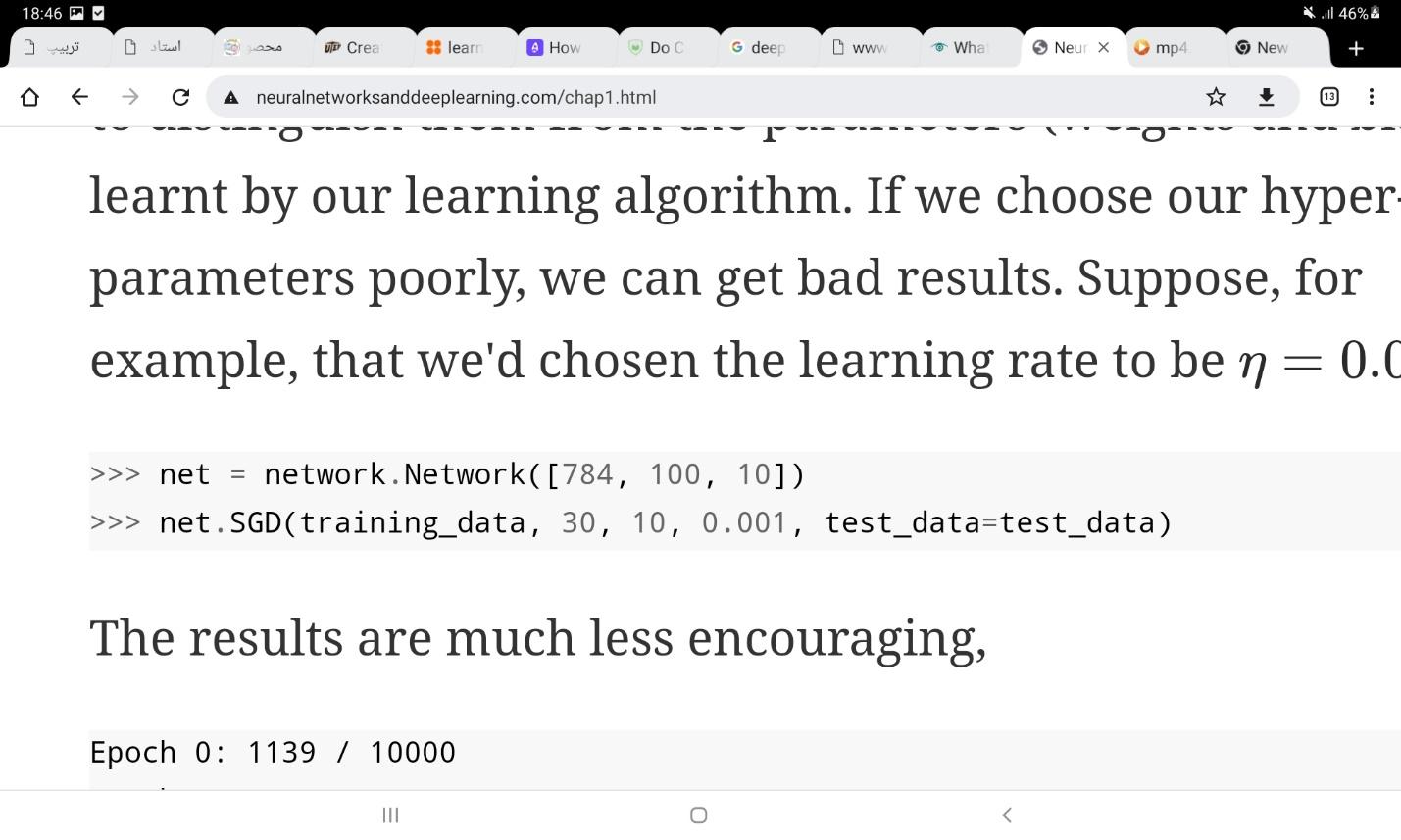
اجرای کد بالا ممکن است چند دقیقه طول بکشد. اگر برای اجرای کد عجله دارید، میتوانید با کم کردن تعداد epoch ها یا تعداد نورونهای پنهان و یا استفاده از قسمتی از مجموعه داده به سرعت اجرای کد بیفزایید. البته استفاده از کتابخانههای آماده شبکههای عصبی بسیار سریعتر نتیجه میدهند و کدهای بالا تنها برای فهم عملکرد شبکههای ابتدایی آورده شدهاند. همچنین زمانی که یک شبکه کاملا آموزش دید، استفاده از آن برای گرفتن خروجی، زمان بسیار کمتری نیاز دارد؛ و تنها فرآیند آموزش است که زمان زیادی میطلبد. شکل زیر خروجی نهایی شبکه بالا را در مساله تشخیص ارقام دستنوشته نشان میدهد. همانطور که مشاهده میشود شبکه موفق شده است تا بعد از 30 مرحله به دقت بالای 95 درصد دست یابد.
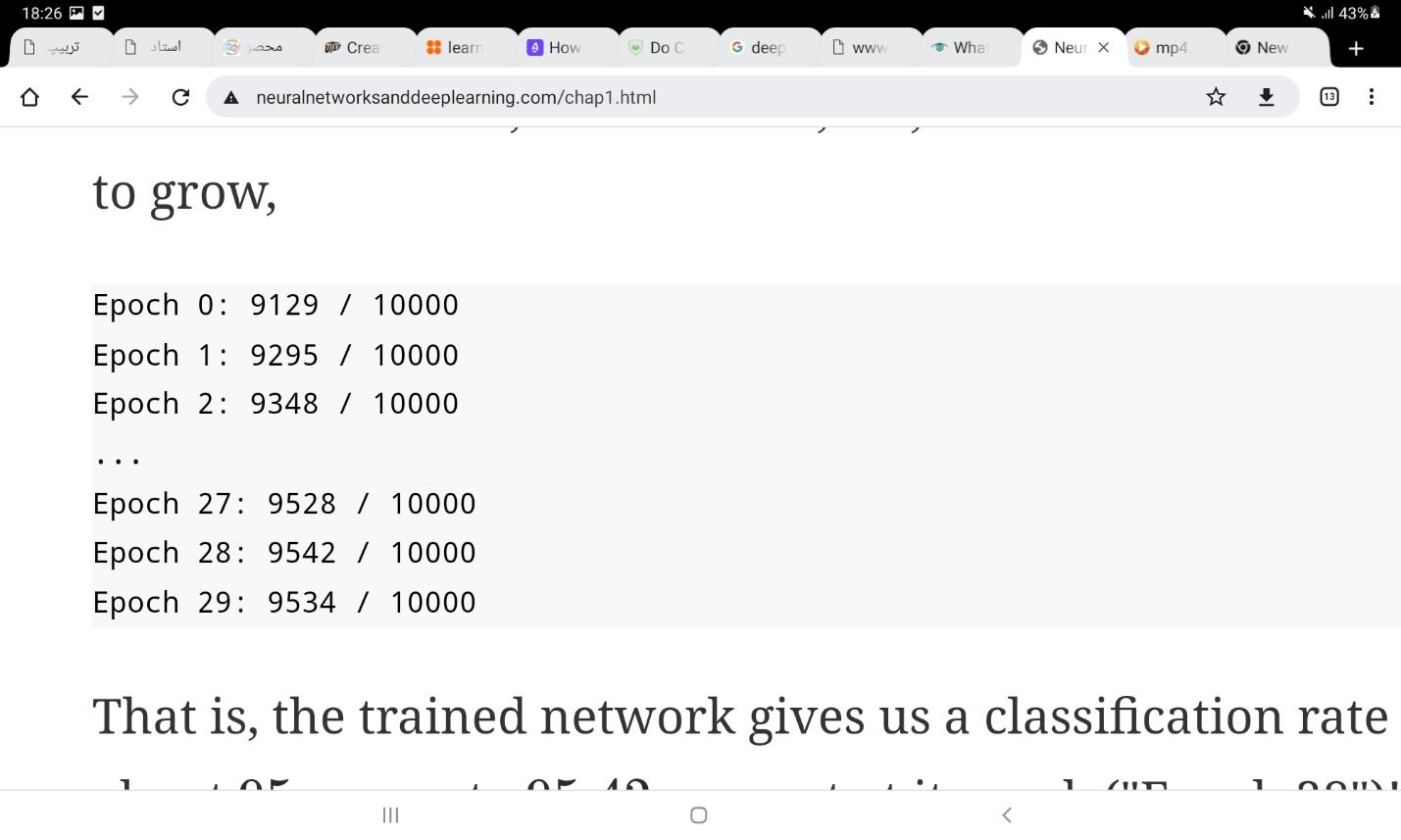
دقت کنید که خروجیهای شبکه با نتایج اجرای شما کاملا یکسان نیستند، زیرا مقادیر اولیه متغیرهای شبکه به طور تصادفی انتخاب میشوند. در صورتی که تعداد نورونهای پنهان به 100 افزایش یابد، دقت شبکه به بالای 96 درصد میرسد. تعداد این نورونها، تعداد لایههای پنهان، اندازه دسته نمونهها در هر بار بروزرسانی، تعداد مراحل آموزش و نرخ یادگیری همگی ابرمتغیرها (hyper-parameters) در مدل هستند و میتوانند توسط مجموعه داده ارزیابی (evaluation set) که بخشی از مجموعه داده آموزشی است، یاد گرفته شوند. انتخاب این متغیرها بسیار حائز اهمیت است. برای مثال اگر در کد بالا نرخ یادگیری برابر با 0.001 انتخاب شود، دقت شبکه در نهایت به 21 درصد میرسد! این در حالی است که شبکههای عصبی بهینهای طراحی شدهاند که بر روی مجموعه داده MNIST به دقتی بالای 99 درصد دست یافتهاند. این شبکهها توسط معماریهای پیشرفتهتر قابل پیادهسازی هستند.
منبع
Michael A. Nielsen, “Neural Networks and Deep Learning”, Determination Press, 2015.


نظرات