هر آن چیزی که در مورد الگوریتم تقویت گرادیان لازم است بدانید

اخبار

مقدمه

تقویت گرادیان یکی از محبوب‌ترین الگوریتم‌های یادگیری ماشین برای مجموعه‌داده‌های جدولی است. این الگوریتم می‌تواند هر رابطۀ غیرخطی‌ای را بین متغیر هدف و متغیرهای مستقل پیدا کند و توانایی بسیار خوبی در مدیریت خودکار مقادیر گمشده، نمونه‌های پرت، و متغیرهای گسسته دارد. در حالی که می‌توانید با استفاده از برخی از کتابخانه‌های محبوب پایتون مانند XGBoost یا LightGBM بدون دانستن جزئیات الگوریتم، از الگوریتم تقویت‌ گرادیان استفاده کنید، برای درک کامل الگوریتم لازم است تا بدانید که وقتی پارامترهای مدل را تنظیم می‌کنید، یا تابع خطا را تغییر می‌دهید، چه اتفاقاتی درون مدل می‌افتد.

این پست قصد دارد تمام جزئیات الگوریتم، به ویژه رویکرد رگرسیونی آن را با ذکر ریاضیات و کدهای پایتون مربوط به آن در اختیار شما قرار دهد.

مثال

تقویت گرادیان یکی از انواع روش‌های یادگیری گروهی است که در آن چندین مدل ضعیف ایجاد می‌کنید و در نهایت آن‌ها را با هم ترکیب می‌کنید تا در مجموع عملکرد بهتری داشته باشید.

در این بخش با استفاده از مثال زیر، که در آن x و y با یکدیگر نوعی رابطۀ غیرخطی دارند، درخت‌های رگرسیونی تقویت‌کنندۀ گرادیان را گام‌‌به‌گام می‌سازیم تا به‌طور مستقیم درک کنیم که این الگوریتم چگونه کار می‌کند. در شکل 1 رابطۀ غیرخطی متغیر مستقل و هدف نمایش داده شده‌است.

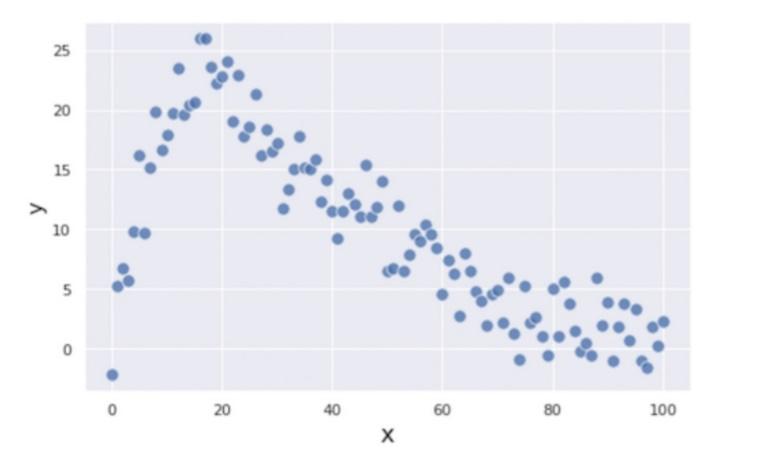
$C:\Users\asus\Downloads\IMG_20231022_140355.jpg$

اولین گام، پیش‌بینی بسیار ساده‌لوحانۀ متغیر هدف است. تابع پیش‌بینی‌کنندۀ اولیۀ را به‌ صورت میانگین متغیر معرفی می‌کنیم:

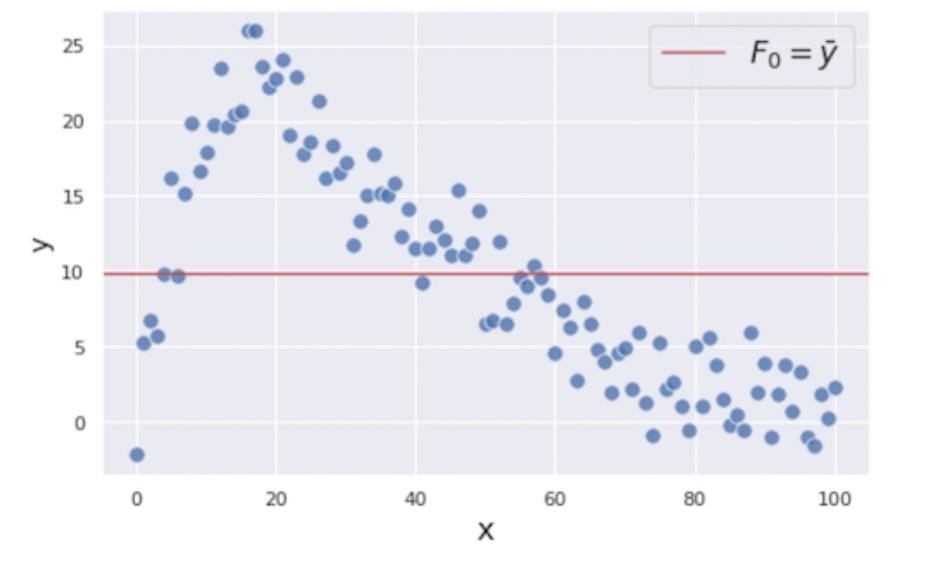
$C:\Users\asus\Downloads\IMG_20231022_140943.jpg$

ممکن است فکر کنید که استفاده از تابع میانگین برای انجام پیش‌بینی بیش از حد ساده‌انگارانه است، اما نگران نباشید. با اضافه کردن مدل‌های ضعیف بیشتر به این فرایند، پیش‌بینی خود را بهبود خواهیم داد.

برای بهبود پیش‌بینی‌مان، روی باقی‌مانده‌ها‌ی (یعنی خطاهای پیش‌بینی) مرحلۀ اول تمرکز می‌کنیم؛ زیرا این همان چیزی است که می‌خواهیم آن را به حداقل برسانیم تا پیش‌بینی بهتری داشته باشیم. باقی‌ماندۀ مرحلۀ اول را می‌نامیم و آن را به‌صورت خطوط آبی عمودی نمایش می‌دهیم (شکل 3).

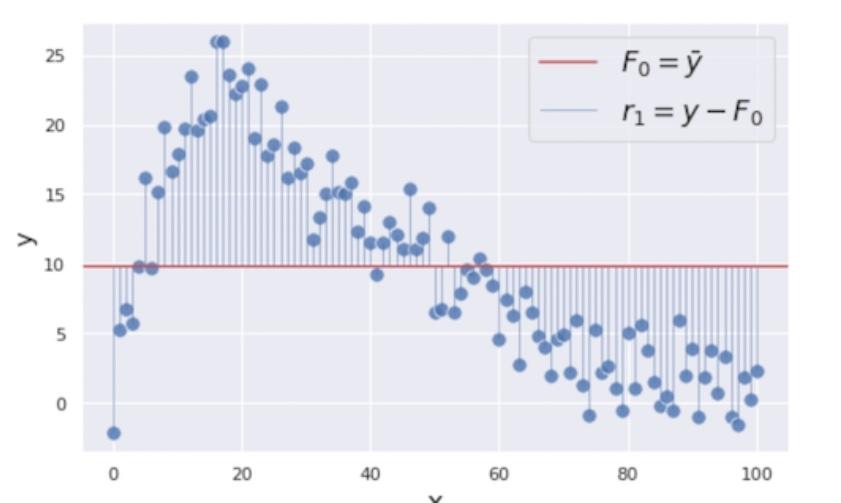
$C:\Users\asus\Downloads\IMG_20231022_141639.jpg$

برای به حداقل رساندن این باقی‌مانده‌ها، یک مدل درخت رگرسیونی دیگر با x به‌عنوان متغیر مستقل و به‌عنوان متغیر هدف آن می‌سازیم.

مزیت ساخت چنین مدلی این است که ضمن آن می‌توانیم با ساخت یک مدل ضعیف اضافه، الگوهایی بین x و پیدا کنیم و با استفاده از آن، باقی‌مانده‌ها را کاهش دهیم.

برای ساده کردن نمایش در شکل‌ها، درخت‌های بسیار ساده‌ای را می‌سازیم که هر کدام فقط دارای یک افراز و دو گره پایانی هستند. به این درخت‌ها، کُندۀ تصمیم گفته می‌شود. لطفاً توجه داشته باشید که درخت‌های تقویت‌کنندۀ گرادیان معمولاً درخت‌هایی کمی عمیق‌تر مانند درخت‌هایی با 8 الی 32 گره پایانی هستند.

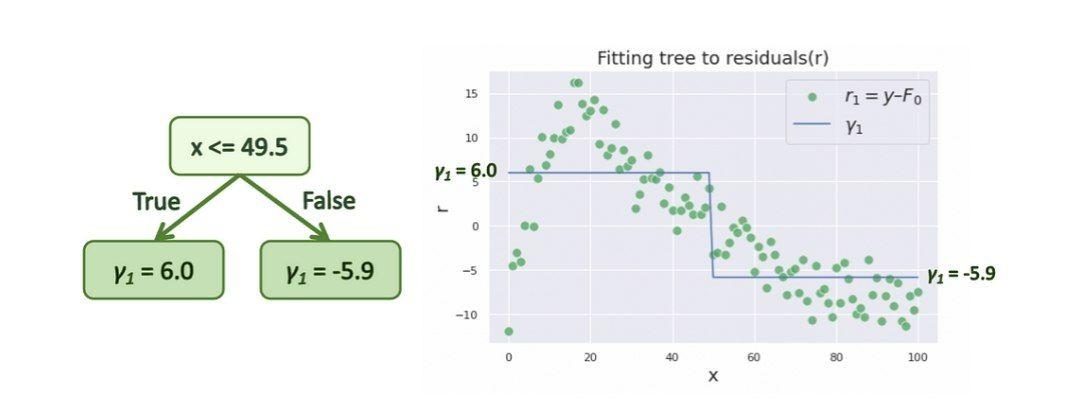
در اینجا اولین کندۀ تصمیم را ایجاد می‌کنیم که باقی‌مانده‌ها را با دو مقدار متفاوت پیش‌بینی می‌کند. از برای نشان دادن پیش‌بینی استفاده می‌کنیم. $C:\Users\asus\Downloads\-5881818314869686408_121.jpg$

پیش‌بینی به پیش‌بینی اولیۀ اضافه می‌شود تا باقی‌مانده‌ها را کاهش دهد. در واقع الگوریتم تقویت گرادیان را به‌صورت مستقیم به اضافه نمی‌کند؛ زیرا این کار باعث می‌شود که مدل روی داده‌های آموزشی دچار بیش‌برازش شود. درعوض،γ با نرخ یادگیری که بین 0 و 1 متغیر است، تعدیل می‌شود و سپس به تابع اضافه می‌شود:

در این مثال، ما از نرخ یادگیری نسبتاً بزرگ استفاده می‌کنیم تا درک فرایند بهینه‌سازی سریع‌تر انجام شود، اما در عمل معمولاً برای این ابرپارامتر مقادیر بسیار کوچک‌تری مانند 0.1 در نظر گرفته می‌شود.

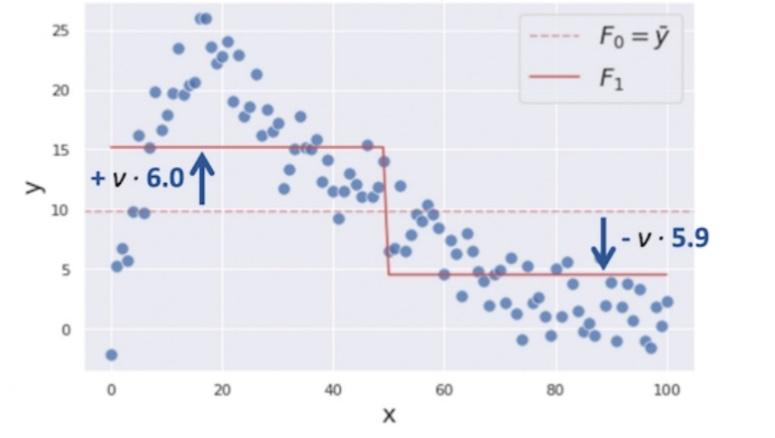
پس از به‌روزرسانی، تابع پیش‌بینی ترکیبی به‌صورت زیر درمی‌آید:

در شکل 5 فرم هندسی نمایش داده شده‌است.

$C:\Users\asus\Downloads\IMG_20231022_144954.jpg$

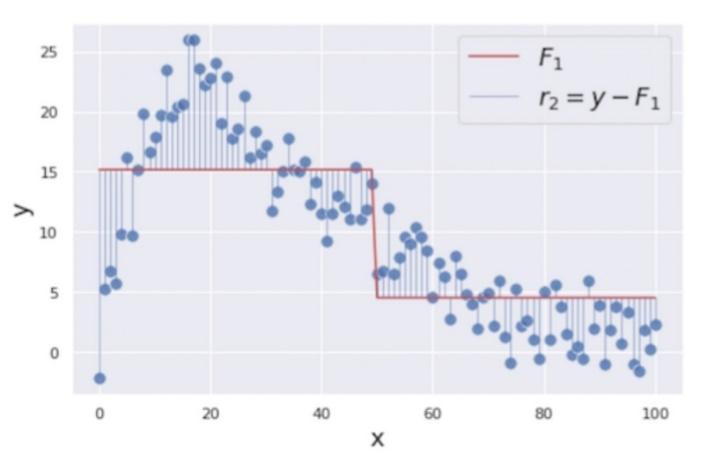
باقی‌مانده‌های به‌روزرسانی‌شدۀ در شکل 6 نشان داده شده‌است:

$C:\Users\asus\Downloads\IMG_20231022_145355.jpg$

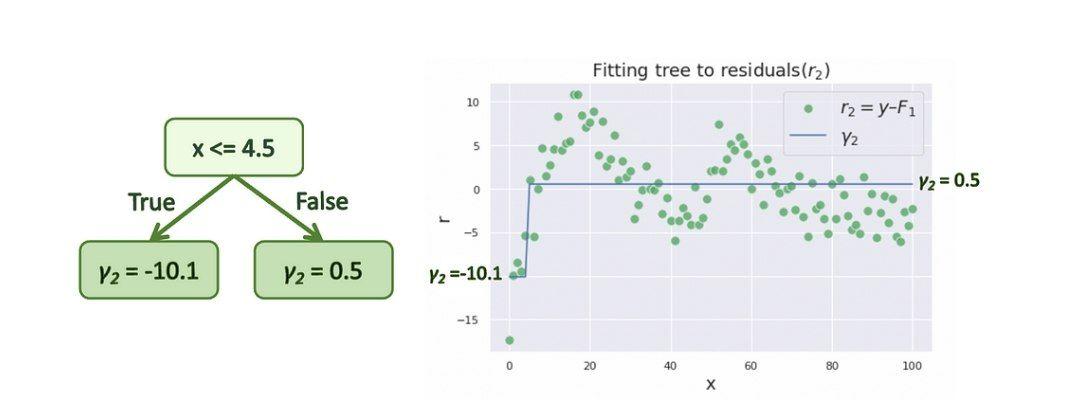
در مرحله بعد، کندۀ جدیدی را با استفاده از همان متغیرهای مستقل قبلی و باقی‌مانده‌های به‌روزرسانی‌شدۀ به عنوان متغیر هدف ایجاد می‌کنیم. کندۀ تصمیم ایجاد‌شده به‌صورت زیر است: $C:\Users\asus\Downloads\-5883971828651768588_121.jpg$

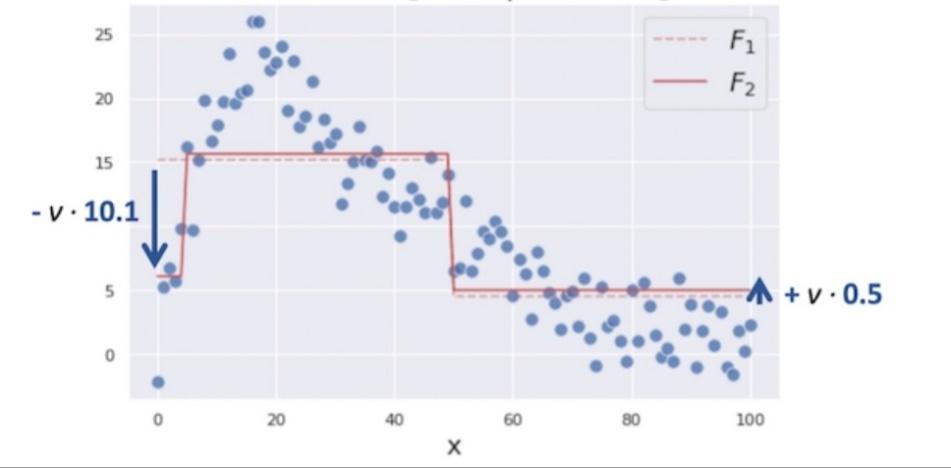
سپس پیش‌بینی ترکیبی قبلی را با پیش‌بینی کندۀ جدید به‌روزرسانی می‌کنیم. $C:\Users\asus\Downloads\IMG_20231022_153851.jpg$

این مراحل را تا زمانی که دقت مدل افرایش می‌یابد، تکرار می کنیم. شکل‌های زیر روند بهبود عملکرد را از تکرار 0 تا 6 تکرار نشان می‌دهند.

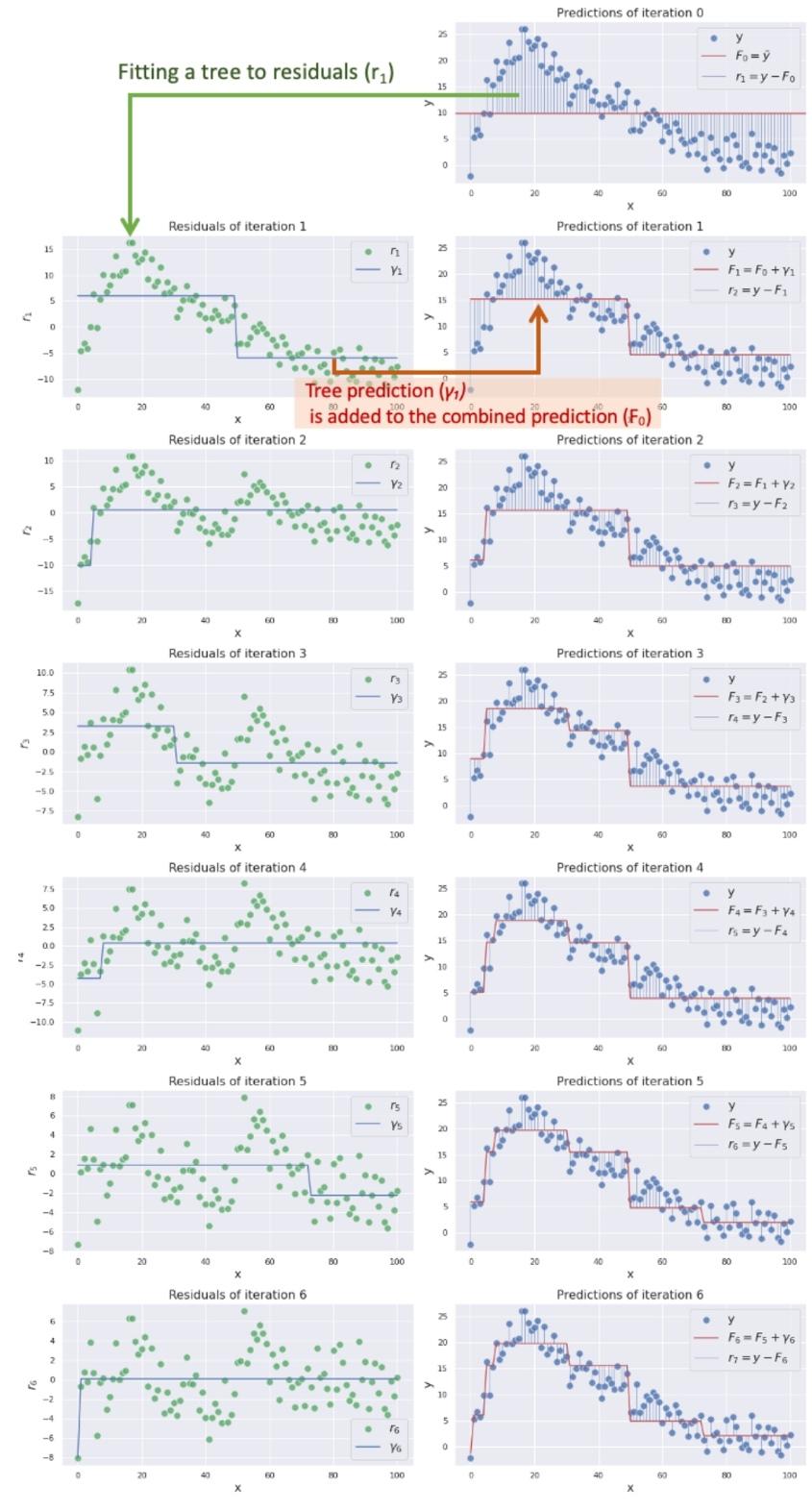
$C:\Users\asus\Downloads\IMG_20231022_154022.jpg$

در شکل 9 می‌توانید ببینید که پیش‌بینی ترکیبی به هدف ما نزدیک و نزدیک‌تر می‌شود زیرا کنده‌های بیشتری را در مدل دخیل می‌کنیم. الگوریتم تقویت گرادیان به این صورت و با ترکیب چندین مدل ضعیف می‌تواند اهداف پیچیده را پیش‌بینی کند.

ریاضیات الگوریتم

در این بخش به جزئیات ریاضی الگوریتم می‌پردازیم. در شکل 10 کل الگوریتم به بیان فرمول‌های ریاضی آمده‌است.

$C:\Users\asus\Downloads\-5883971828651768592_121.jpg$

بیایید روابط بالا را خط به خط بررسی کنیم.

مرحلۀ اول

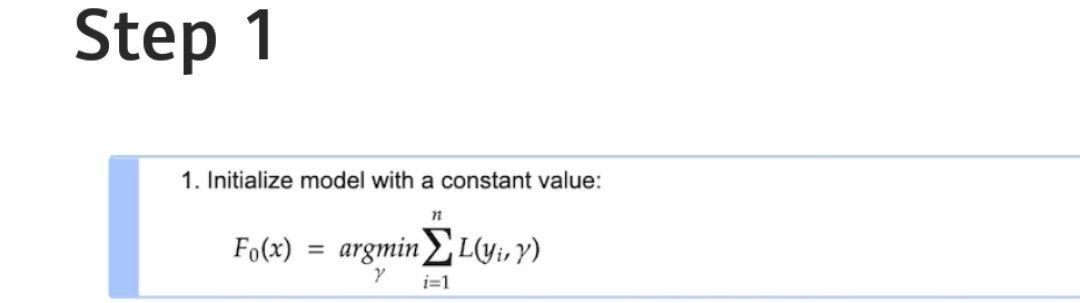
$C:\Users\asus\Downloads\-5883971828651768593_121.jpg$

اولین مرحله ایجاد یک تابع پیش‌بینی اولیه با مقدار ثابت است. تابع زیان است که در حالت رگرسیونی معمولاً آن را برابر با مجذور خطا در نظر می‌گیریم:

به این معنی است که ما به دنبال مقداری برای هستیم که را به حداقل برساند. در واقع می‌خواهیم پیش‌بینی را با استفاده از تابع زیان به دست بیاوریم. برای یافتن مقداری برای که را به حداقل می‌رساند، از نسبت به مشتق می‌گیریم.

ما به دنبال مقداری برای γ هستیم که را برابر با 0 می‌کند:

معلوم شد که مقدار که را به حداقل می‌رساند، میانگین است. به همین دلیل است که ما از میانگین برای پیش‌بینی اولیه‌ در مثال قبلی استفاده کردیم.

مرحلۀ دوم

$C:\Users\asus\Downloads\-5883971828651768601_121.jpg$

کل بخش‌های گام دوم از 2-1 تا 2-4، M بار تکرار می‌شوند. M نشان‌دهندۀ تعداد درختانی است که ایجاد می‌کنیم و m نشان‌دهندۀ اندیس هر درخت است.

بخش اول $C:\Users\asus\Downloads\-5883971828651768607_121.jpg$

با مشتق‌گیری از تابع زیان نسبت به پیش‌بینی قبلی () و ضرب آن در 1-، باقی‌مانده‌های را محاسبه می‌کنیم. همان‌طور که در اندیس‌ها می‌بینید، برای تمام نمونه‌ها محاسبه می‌شود. ممکن است تعجب کنید که چرا بهها باقی‌مانده می‌گوییم. این مقادیر در واقع جهت عکس گرادیان هستند که جهت (+/-) و مقداری را نشان می‌دهند که در آن تابع زیان مدل می‌تواند به حداقل برسد.این تکنیک، که در آن از گرادیان برای به حداقل رساندن تابع زیان در مدل استفاده می‌کنیم، بسیار شبیه به تکنیک گرادیان کاهشی است که معمولاً برای بهینه‌سازی شبکه‌های عصبی به کار می‌رود.

بیایید باقی‌مانده‌ها را محاسبه کنیم. در معادله به معنای پیش‌بینی مرحله قبل است که آن را در اولین تکرار با نمایش می‌دهیم. معادله را برای باقی‌ماندۀ حل می‌کنیم:

می‌توانیم 2 را از آن فاکتور بگیریم زیرا عدد ثابت است. بنابراین داریم . این تفاضل خطای مدل را نشان می‌دهد و حالا واضح است که چرا ما آن‌ها را باقی‌مانده می‌نامیم. این معادله (7) همچنین بینش جالبی دربارۀ این که منفی گرادیان در واقع همان باقی‌مانده‌ها‌ی مدل است به ما می‌دهد.

بخش دوم

$C:\Users\asus\Downloads\-5883971828651768611_121.jpg$

شکل 14: بخش دوم مرحلۀ دوم الگوریتم

در شکل 14 j نشان‌دهندۀ گره پایانی (برگ) درخت، m نشان‌دهندۀ اندیس درخت، و J بیانگر تعداد کل برگ‌ها است.

بخش سوم $C:\Users\asus\Downloads\-5883971828651768613_121.jpg$

در شکل 15 ما به دنبال مقداری برای هستیم که تابع زیان را در هر گره ترمینال به حداقل برساند. به این معنی است که ما در حال تجمیع مقدار زیان در تمام نمونه‌هایی هستیم که به گره پایانی تعلق دارند‌.

بیایید تابع زیان را نیز به معادله اضافه کنیم.

سپس، مقداری را برای می‌یابیم که مشتق را برابر با صفر ‌کند.

توجه داشته باشید که به معنای تعداد نمونه‌ها در گره پایانی است. این بدان معناست که بهینه که تابع زیان را به حداقل می‌رساند، میانگین باقی‌مانده‌های در گره پایانی است. به عبارت دیگر، همان پیش‌بینی درخت‌ اول رگرسیونی است که میانگین مقادیر هدف (در مورد ما، باقی‌مانده‌ها) را به‌عنوان پیش‌بینی برمی‌گرداند.

بخش چهارم

$C:\Users\asus\Downloads\-5883971828651768620_121.jpg$

شکل 16: بخش چهارم مرحلۀ دوم الگوریتم

در مرحلۀ آخر، پیش‌بینی مدل ترکیبی را به‌روزرسانی می‌کنیم. در رابطۀ بالا به این معنی است که اگر نمونۀ در گره پایانی قرار بگیرد، مقدار را انتخاب می‌کنیم. از آنجایی که تمام گره‌های پایانی منحصربه‌فرد هستند، هر نمونه تنها در یک گره پایانی قرار می‌گیرد و مقدار مربوطه به پیش‌بینی قبلی اضافه می‌شود و به این ترتیب پیش‌بینی به‌روزرسانی می‌شود.

همان‌طور که در بخش قبل گفته شد، نرخ یادگیری است که بین 0 و 1 مقدار می‌گیرد و میزان مشارکت پیش‌بینی کندۀ را در پیش‌بینی ترکیبی مشخص می‌کند. نرخ یادگیری کمتر، اثر پیش‌بینی کندۀ تصمیم را کاهش می‌دهد. نرخ یادگیری اساساً احتمال بیش‌برازش مدل روی داده‌های آموزشی را کاهش می‌دهد.

اکنون ما تمام مراحل را بیان کرده‌ایم. برای به دست آوردن بهترین عملکرد مدل، مرحله دوم را مرتبه تکرار می‌کنیم، که به معنای افزودن درخت اضافی به مدل ترکیبی است.

در مسائل واقعی معمولا بیش از 100 درخت اضافی را در نظر می‌گیرند تا مدل به بهترین عملکرد خودش برسد.

پیاده‌سازی در محیط پایتون

در این بخش، ما ریاضیاتی را که به تازگی بررسی کردیم را به یک کد پایتون قابل اجرا ترجمه می‌کنیم تا به ما در درک بیشتر الگوریتم کمک کند. از DecisionTreeRegressor از کتابخانۀscikit-learn برای ساخت درخت‌ها استفاده می‌کنیم که به ما کمک می‌کند به جای الگوریتم درخت تصمیم، روی خود الگوریتم تقویت گرادیان تمرکز کنیم. همچنین خودمان این الگوریتم را پیاده‌سازی می‌کنیم و نتیجۀ آن را با پیاده‌سازی آمادۀ کتابخانۀ scikit-learn مقایسه می‌کنیم.

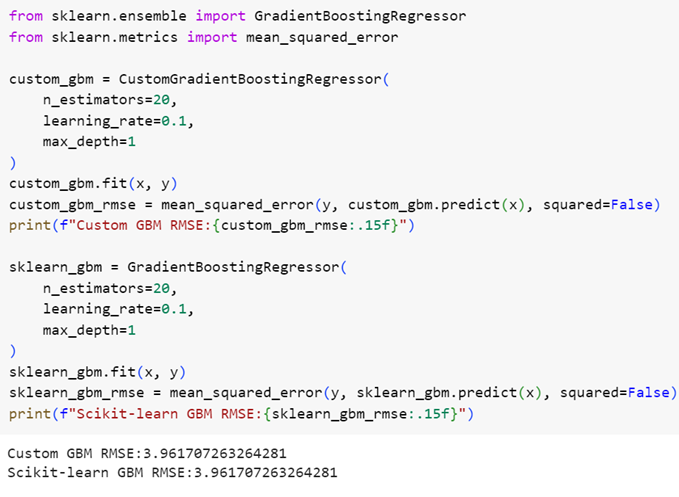
شکل 18: مقایسه‌ی عملکرد مدل پیاده‌سازی‌شده با مدل آماده‌ی کتابخانه‌ی scikit-learn

همان‌طور که در شکل 18 مشاهده می‌کنید پیاده‌سازی ما با پیاده‌سازی کتابخانۀ scikit-learn عملکرد مشابهی دارد.

مجموعۀ کامل کدهای استفاده‌شده در این پست در نوت‌بوک همراه این پست آورده‌شده‌است.

امیدواریم این پست برایتان مفید بوده باشد.

منبع

https://towardsdatascience.com/all-you-need-to-know-about-gradient-boosting-algorithm-part-1-regression-2520a34a502

به این مطلب امتیاز دهید

نظرات

جهت ارسال نظر و دیدگاه خود باید ابتدا وارد سایت شوید

پروفایل‌های مرتبط

مهدی نورایی

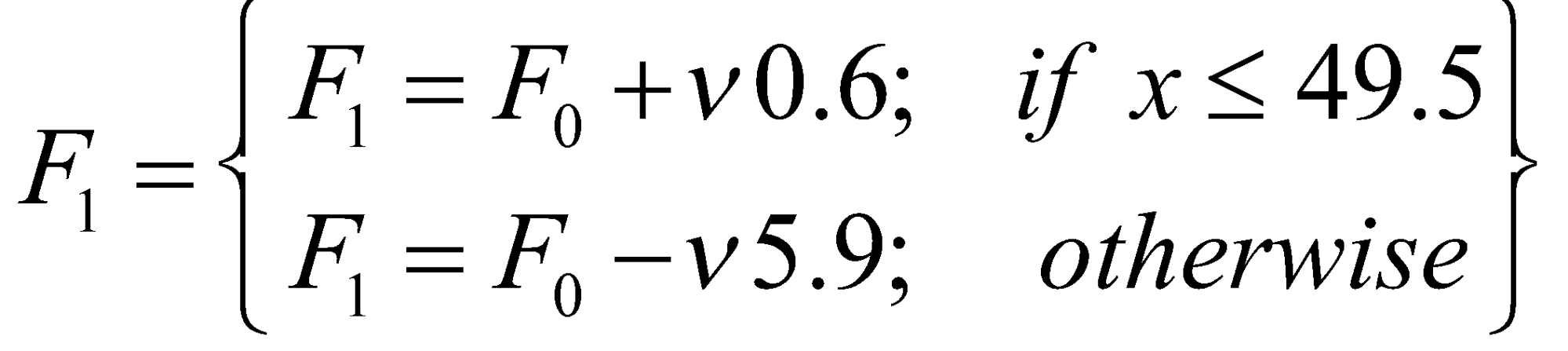
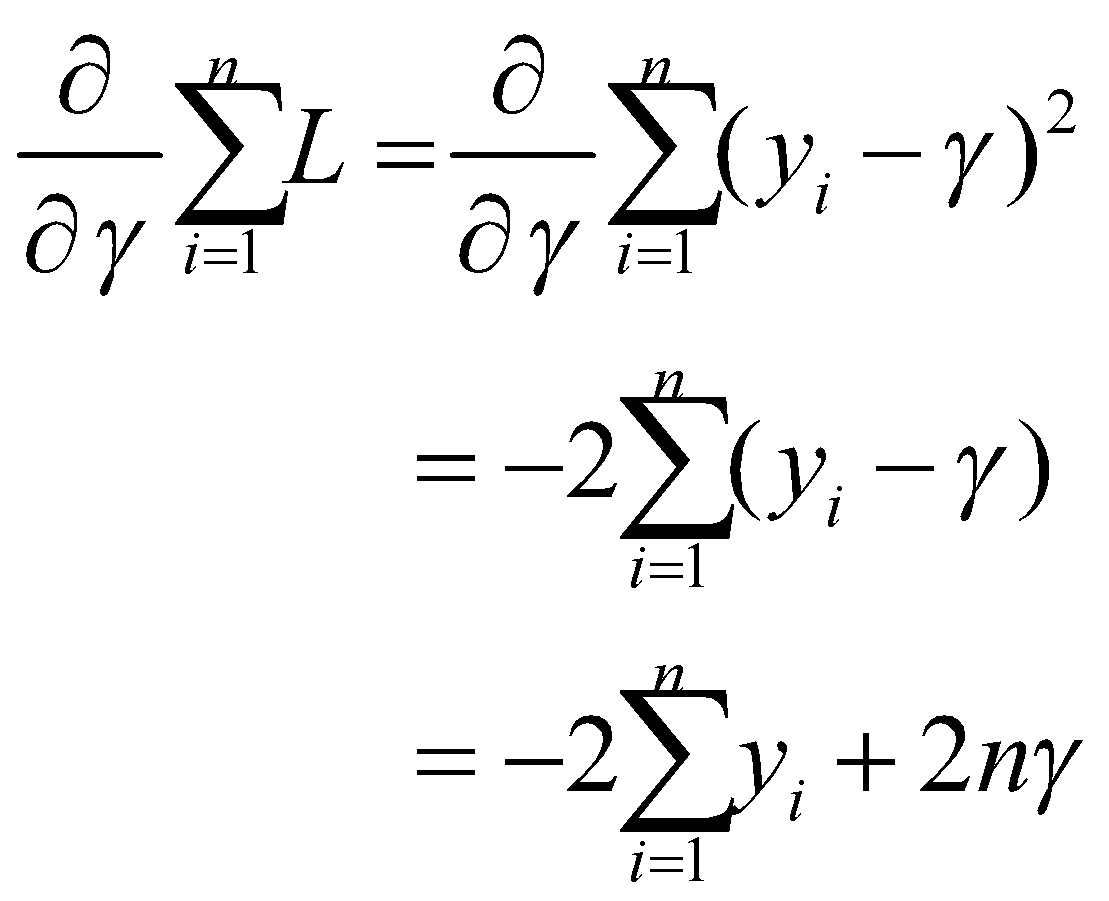
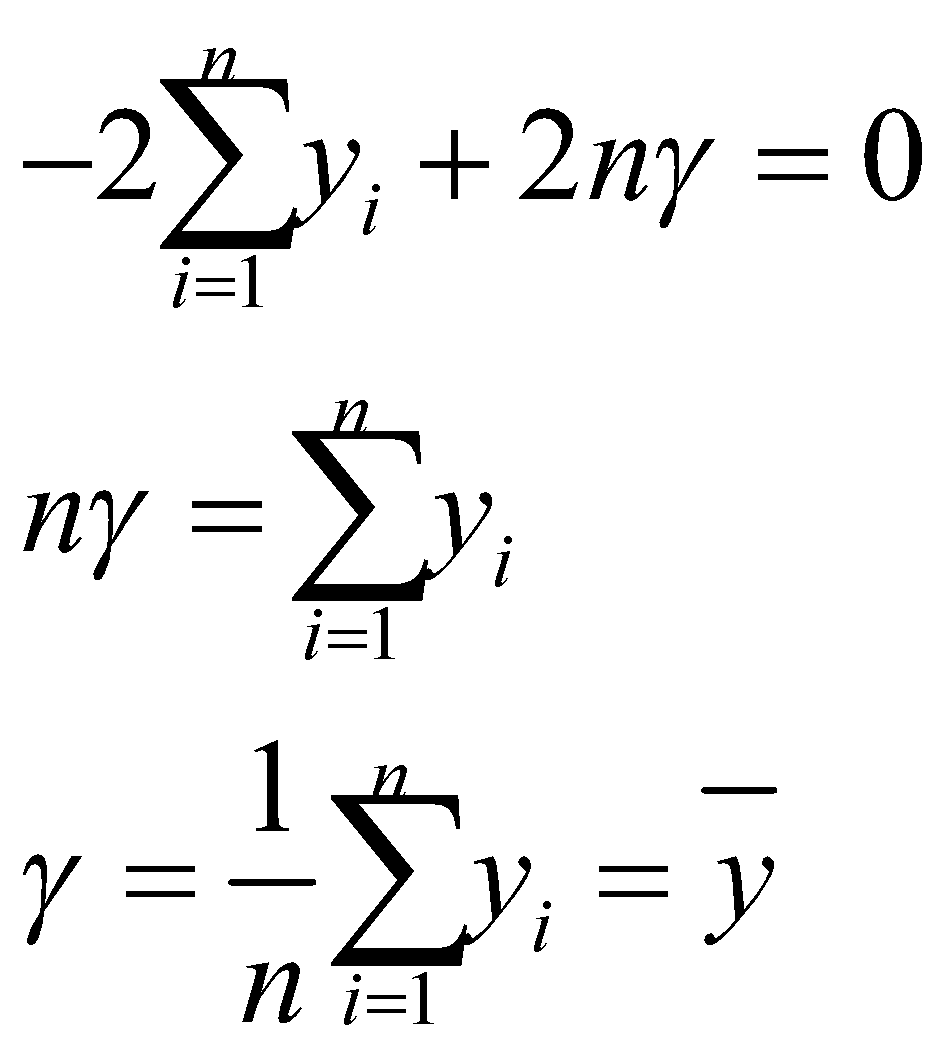
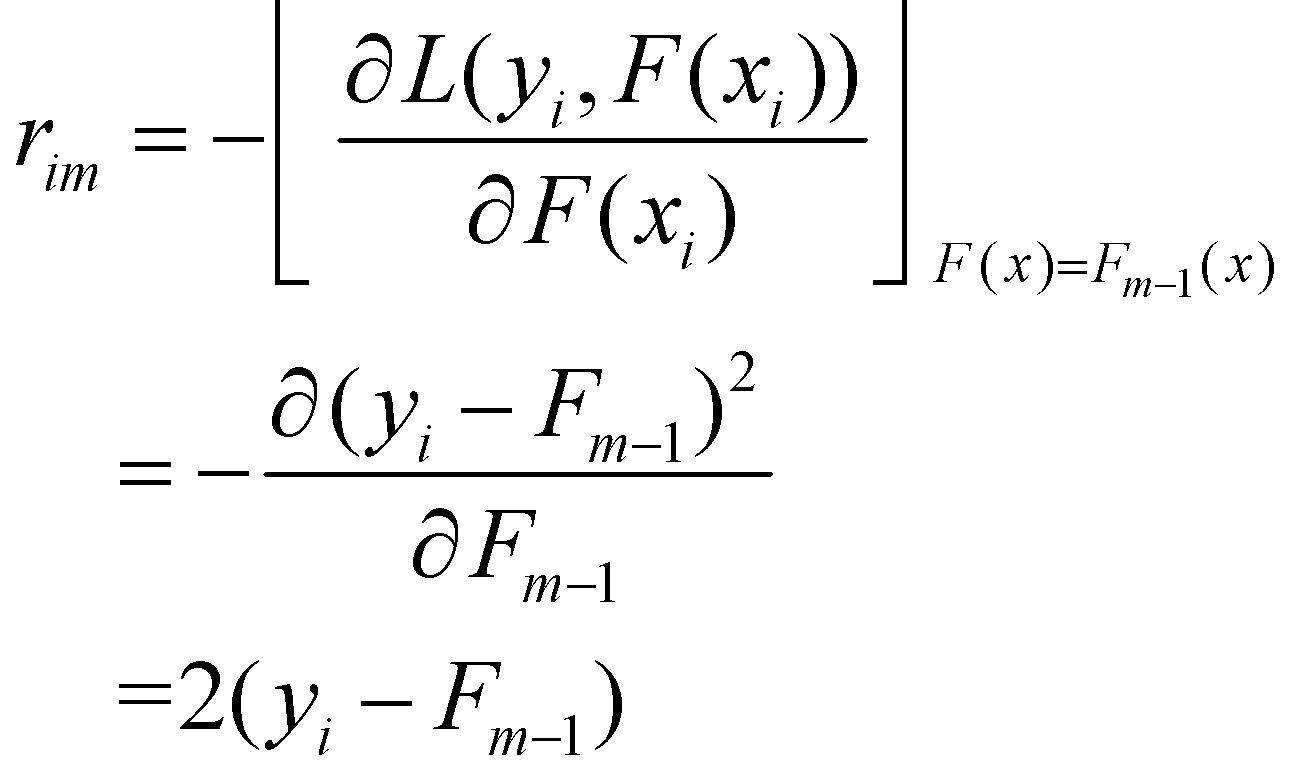
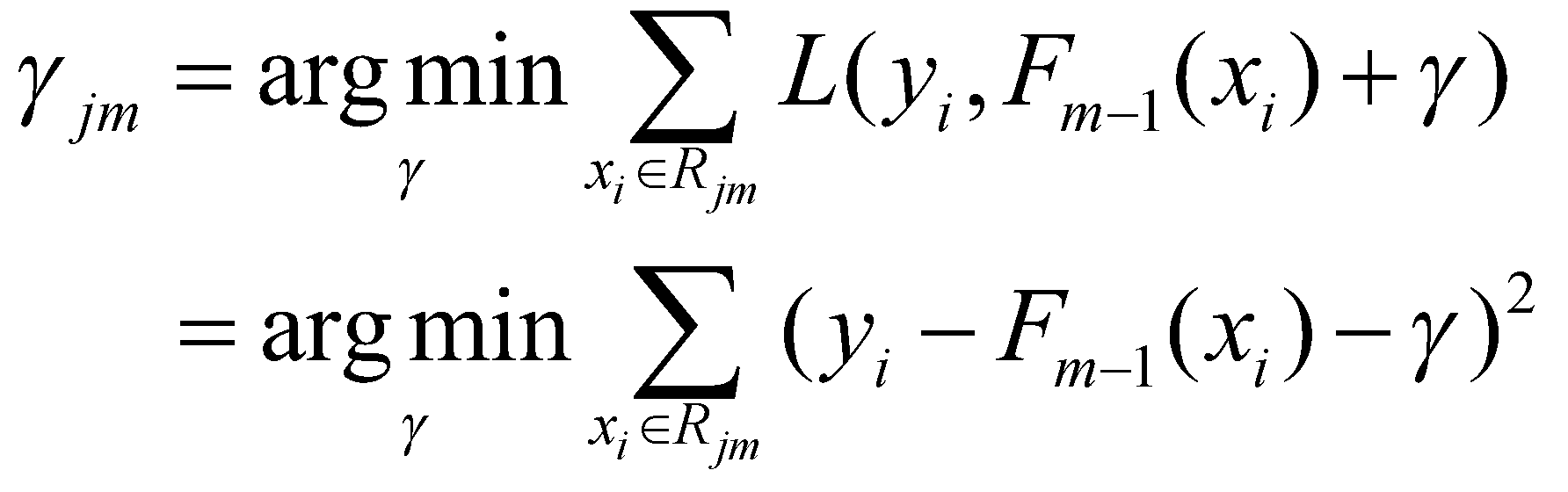
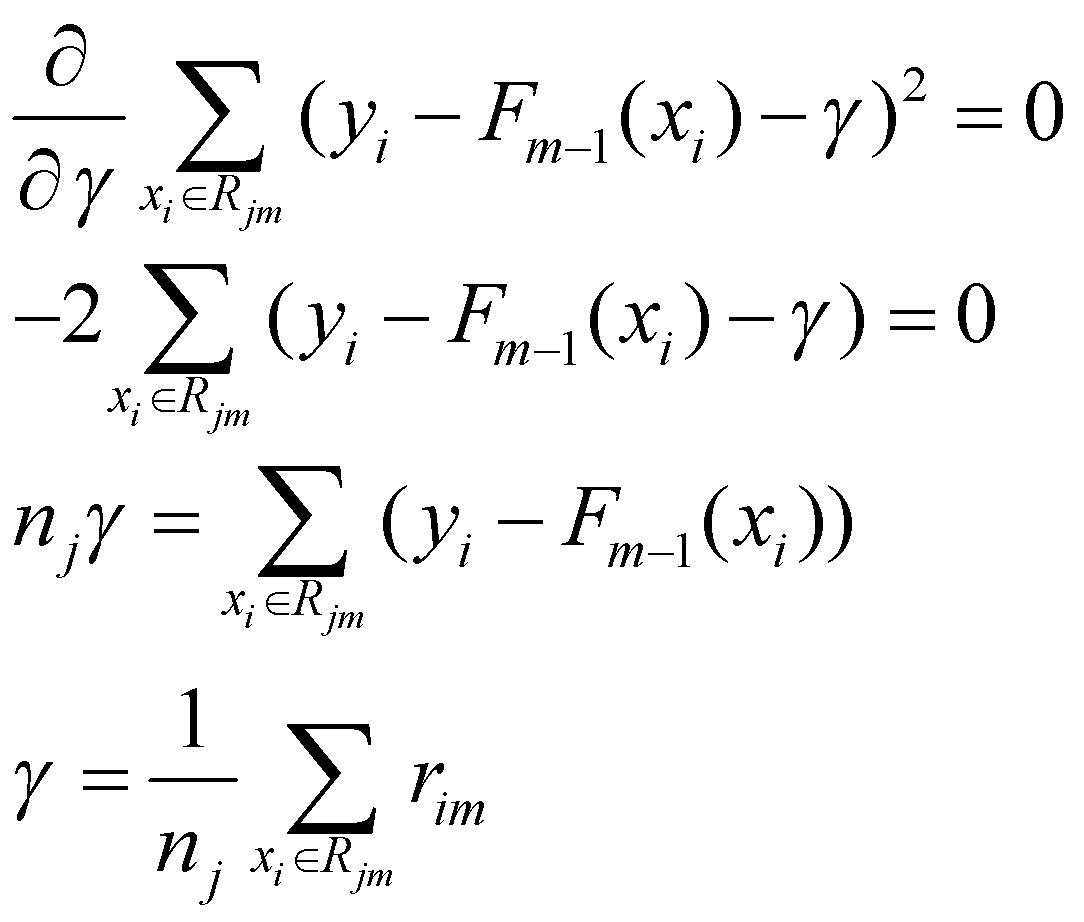
نظرات